Влучність та повнота
В розпізнаванні образів, інформаційному пошуку та класифікації, влу́чність[1] (англ. precision, яку також називають прогностичною значущістю позитивного результату[2]) є часткою релевантних зразків серед знайдених, тоді як повнота́[1] (англ. recall, відома також як чутливість) є часткою загального числа позитивних зразків, яку було дійсно знайдено. Як влучність, так і повнота, відтак ґрунтуються на розумінні та мірі релевантності. Влучність не слід плутати з точністю (англ. accuracy), яка є часткою правильно спрогнозованих результатів, як позитивних, так і негативних.[3] Влучність стосується лише позитивних результатів.
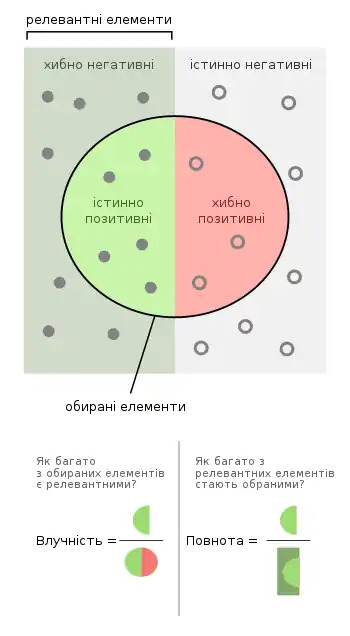
Нехай комп'ютерна програма для розпізнавання собак на фотографіях виявила 8 собак на зображенні, що містить 10 котів та 12 собак (власне релевантних елементів). Серед 8 ідентифікованих як собаки 5 і справді є собаками (істинно позитивні), тоді як інші 3 є котами (хибно позитивні). 7 собак було пропущено (хибно негативні), а 7 котів було виключено правильно (істинно негативні). Влучність цієї програми становить 5/8 (істинно позитивні / всі позитивні), тоді як повнота — 5/12 (істинно позитивні / релевантні елементи). Коли пошуковий рушій повертає 30 сторінок, лише 20 з яких є релевантними, в той же час виявляючись нездатним повернути 40 додаткових релевантних сторінок, його влучність становить 20/30 = 2/3, тоді як повнота — 20/60 = 1/3. Тож, у цьому випадку, влучність показує, «наскільки правильними є результати», тоді як повнота — «наскільки повними є результати».
Якщо застосовувати підхід перевірки гіпотез зі статистики, в якому, в цьому випадку, нульова гіпотеза полягає в тім, що заданий зразок є нерелевантним, тобто, не собакою, то відсутність помилок першого і другого роду (тобто, ідеальні чутливість та специфічність у 100 % кожна) відповідає, відповідно, ідеальній влучності (без хибно позитивних) та ідеальній повноті (без хибно негативних).
Загальніше, повнота є просто доповненням рівня помилок II роду, тобто, одиниця мінус рівень помилок II роду. Влучність пов'язана з рівнем помилок I роду, але дещо складнішим чином, оскільки вона також залежить від апріорного розподілу спостерігання релевантного, чи нерелевантного зразка.
Наведений вище приклад із котами та собаками містив 8 − 5 = 3 помилки I роду, що давало рівень помилок I роду 3/10, та 12 − 5 = 7 помилок II роду, що давало рівень помилок II роду 7/12. Влучність можливо розглядати як рівень якості, тоді як повноту — як рівень кількості. Вища влучність означає, що алгоритм видає більше релевантних зразків, ніж нерелевантних, а висока повнота означає, що алгоритм видає більшість із релевантних результатів (незалежно від того, чи він також видає й нерелевантні).
Введення
В інформаційному пошуку зразками є документи, а задачею є повернути набір релевантних документів для заданої умови пошуку. Повнота є числом релевантних документів, знайдених пошуком, поділеним на загальне число релевантних документів, які існують, тоді як влучність є числом релевантних документів, знайдених пошуком, поділеним на загальне число знайдених документів, які знайшов цей пошук.
В задачі класифікації, влучністю для певного класу є число істинно позитивних (тобто, число зразків, правильно відмічених як належні до позитивного класу), поділене на загальне число елементів, відмічених як належні до позитивного класу (тобто, суму істинно позитивних та хибно позитивних, що є зразками, неправильно відміченими як належні до позитивного класу). Повноту в цьому контексті визначено як число істинно позитивних, поділене на загальне число елементів, що насправді належать до позитивного класу (тобто, суму істинно позитивних та хибно негативних, що є зразками, як не було відмічено як належні до позитивного класу, але повинно було бути відмічено).
В інформаційному пошуку ідеальна оцінка влучності в 1,0 означає, що кожен з результатів, знайдених пошуком, був релевантним (але не каже нічого про те, чи всі релевантні документи було знайдено), тоді як ідеальна оцінка повноти в 1,0 означає, що цим пошуком було знайдено всі релевантні документи (але не каже нічого про те, як багато було знайдено також і нерелевантних документів).
В задачі класифікації оцінка влучності в 1,0 для класу C означає, що кожен зі зразків, відмічений як належний до класу C, й насправді належить до класу C (але не каже нічого про число зразків з класу C, які не було правильно відмічено), тоді як повнота в 1,0 означає, що кожен зі зразків з класу C було відмічено як належний до класу C (але не каже нічого про те, скільки зразків з інших класів було неправильно відмічено як належні до класу C).
Між влучністю й повнотою часто існує обернена залежність, коли можливо підвищити одну ціною зниження іншої. Наочним прикладом цього компромісу є нейрохірургія. Розгляньмо нейрохірурга, який видаляє ракову пухлину з мозку пацієнта. Нейрохірургові потрібно видалити всі клітини пухлини, оскільки залишені ракові клітини відродять пухлину. І навпаки, нейрохірург мусить не видаляти здорові клітини мозку, оскільки це призведе до порушень функцій мозку пацієнта. Нейрохірург може бути більш розмашистим щодо області мозку, яку він видаляє, щоби забезпечити видалення всіх ракових клітин. Це рішення підвищує повноту, але знижує влучність. З іншого боку, нейрохірург може бути консервативнішим щодо мозку, який він видаляє, щоби забезпечити вилучення лише ракових клітин. Це рішення підвищує влучність, але знижує повноту. Тобто, вища повнота підвищує шанси видалення здорових клітин (негативний результат), і підвищує шанси видалення всіх ракових клітин (позитивний результат). Вища влучність знижує шанси вилучення здорових клітин (позитивний результат), але також знижує шанси видалення всіх ракових клітин (негативний результат).
Зазвичай оцінки влучності та повноти не обговорюють окремо. Натомість, або значення однієї міри порівнюють за фіксованого рівня іншої міри (наприклад, влучність на рівні повноти 0,75), або поєднують обидві в єдину міру. Прикладами мір, що є поєднаннями влучності та повноти, є F-міра (зважене середнє гармонійне влучності та повноти) та коефіцієнт кореляції Меттьюза, що є середнім геометричним скоригованих на шанси варіантів: коефіцієнтів регресії поінформованості (Δp') та маркованості (Δp).[4][5] Точність є зваженим (на зміщення) середнім арифметичним влучності та оберненої влучності, так само як і зваженим (на поширеність) середнім арифметичним повноти та оберненої повноти.[4] Обернена влучність та обернена повнота є просто влучністю та повнотою оберненої задачі, де позитивні та негативні мітки поміняно місцями (як для справжніх класів, так і для передбачуваних міток). Повноту та обернену повноту, або, рівнозначно, істиннопозитивний та хибнопозитивний рівні часто відкладають один проти одного як криві РХП, забезпечуючи принциповий механізм дослідження компромісів робочої точки. Поза інформаційним пошуком застосування повноти, влучності та F-міри вважають хибним, оскільки вони ігнорують істинно негативну комірку таблиці невідповідностей, й ними легко маніпулювати, зміщуючи передбачення.[4] Першу проблему «розв'язують» застосуванням точності, а другу проблему «розв'язують» знижуванням складової шансу та перенормовуванням до каппи Коена, але це більше не дає можливості досліджувати компроміси графічно. Проте, поінформованість та маркованість є каппа-подібними перенормуваннями повноти та влучності,[6] а їхній середній геометричний коефіцієнт кореляції Меттьюза відтак виступає незміщеною F-мірою.
Визначення (в контексті інформаційного пошуку)
В контексті інформаційного пошуку визначення влучності та повноти подають в термінах множини знайдених документів (наприклад, переліку документів, виробленого рушієм вебпошуку для якогось запиту), та множини релевантних документів (наприклад, переліку всіх документів в Інтернеті, що є релевантними для певного предмету), пор. релевантність.[7]
Влучність
В галузі інформаційного пошуку, влучність є часткою знайдених документів, що є релевантними запитові:
- влучність = | {релевантні документи} ∩ {знайдені документи} || {знайдені документи} |
Наприклад, для текстового пошуку на множині документів, влучність є числом правильних результатів, поділеним на число всіх повернених результатів.
Влучність бере до уваги всі знайдені документи, але її також можливо оцінювати на заданому рівні відсікання, враховуючи лише розташовані найвище результати, що повертає система. Таку міру називають «N-влучністю» (англ. precision at n, P@n).
Влучність використовують разом із повнотою, відсотком всіх релевантних документів, який повертає пошук. Ці дві міри іноді використовують разом в оцінці F1 (або F-мірі), щоби забезпечити єдине вимірювання для системи.
Зауважте, що значення та вживання терміну «влучність» (англ. precision) в області інформаційного пошуку відрізняється від визначення точності та прецизійності (англ. accuracy and precision) в межах інших галузей науки та технології.
Повнота
В інформаційному пошуку повнота є часткою релевантних документів, яку вдається успішно знайти.
- повнота = | {релевантні документи} ∩ {знайдені документи} || {релевантні документи} |
Наприклад, для текстового пошуку на множині документів, повнота є числом правильних результатів, поділеним на число результатів, які мало би бути повернуто.
В бінарній класифікації повноту називають чутливістю. Її можливо розглядати як імовірність того, що релевантний документ буде знайдено за запитом.
Досягти повноти 100 % тривіально, якщо повертати у відповідь на запит всі документи. Отже, повнота сама по собі не є достатньою, й потрібно також вимірювати й число нерелевантних документів, наприклад, обчислюючи також і влучність.
Визначення (в контексті класифікації)
Для задач класифікації, терміни істинно позитивні, істинно негативні, хибно позитивні та хибно негативні (див. визначення в помилках першого і другого роду) є порівняннями результатів тестованого класифікатора з надійними зовнішніми судженнями. Терміни позитивні та негативні стосуються передбачень класифікатора (які іноді називають очікуванням), а терміни істинно та хибно стосуються того, чи це передбачення відповідає зовнішньому судженню (іноді відомому як спостереження).
Визначмо експеримент із П позитивними зразками та Н негативними зразками для якоїсь умови. Ці чотири результати може бути виражено таблицею спряженості або матрицею невідповідностей 2×2 наступним чином:
| Справжній стан | ||||||
| загальна сукупність | позитивний стан | негативний стан | поширеність = Σ позитивних станівΣ загальної сукупності | точність = Σ істинно позитивних + Σ істинно негативнихΣ загальної сукупності | ||
| позитивний прогнозований стан |
істинно позитивний | хибно позитивний, помилка I роду |
прогностична значущість позитивного результату (ПЗ+), влучність = Σ істинно позитивнихΣ позитивних прогнозованих станів | рівень хибного виявляння (РХВ) = Σ хибно позитивнихΣ позитивних прогнозованих станів | ||
| негативний прогнозований стан |
хибно негативний, помилка II роду |
істинно негативний | рівень хибного пропускання (РХП) = Σ хибно негативнихΣ негативних прогнозованих станів | прогностична значущість негативного результату (ПЗ-) = Σ істинно негативнихΣ негативних прогнозованих станів | ||
| істиннопозитивний рівень (ІПР), повнота, чутливість, ймовірність виявлення, потужність = Σ істинно позитивнихΣ позитивних станів | хибнопозитивний рівень (ХПР), побічний продукт, ймовірність хибної тривоги = Σ хибно позитивнихΣ негативних станів | відношення правдоподібності позитивного результату (ВП+) = ІПРХПР | діагностичне відношення шансів (ДВШ) = ВП+ВП− | міра F1 = 2 · влучність · повнотавлучність + повнота | ||
| хибнонегативний рівень (ХНР), коефіцієнт невлучання = Σ хибно негативнихΣ позитивних станів | специфічність, вибірність, істиннонегативний рівень (ІНР) = Σ істинно негативнихΣ негативних станів | відношення правдоподібності негативного результату (ВП-) = ХНРІНР | ||||
Джерела: Fawcett (2006),[10] Powers (2011),[11] Ting (2011),[12] CAWCR,[13] D. Chicco & G. Jurman (2020) (2020),[14] Tharwat (2018),[15] Смоляр та ін. (2013),[8] Коваль та ін. (2016),[3] Швець (2015),[2] Гущин та Сич (2018),[1] Мірошниченко та Івлієва (2019).[9] |
Влучність та повноту тоді визначають як[16]
- Влучність = ІПІП + ХП
- Повнота = ІПІП + ХН
Повноту в цьому контексті також називають істиннопозитивним рівнем, або чутливістю, а влучність також називають Прогностична значущість позитивного результату (ПЗ+). До інших пов'язаних мір, які використовують у класифікації, належать істиннонегативний рівень, та точність. Істиннонегативний рівень також називають специфічністю.
- Істиннонегативний рівень = ІНІН + ХП
Незбалансовані дані
- Точність = ІП + ІНІП + ІН + ХП + ХН
Для незбалансованих наборів даних точність може бути оманливою метрикою. Розгляньмо вибірку з 95 негативними та 5 позитивними значеннями. Класифікування всіх значень як негативних у цьому випадку дає оцінку точності 0,95. Існує багато метрик, які не страждають на цю проблему. Наприклад, збалансована точність (ЗТ, англ. balanced accuracy, bACC)[17] унормовує істинно позитивні та істинно негативні передбачення числом позитивних та негативних зразків відповідно, й ділить їхню суму навпіл:
- Збалансована точність = ІПР + ХПР2
Для попереднього прикладу (95 негативних та 5 позитивних зразків), класифікування всіх як негативних дає оцінку збалансованої точності 0,5 (максимальною оцінкою ЗТ є одиниця), що є рівнозначним математичному сподіванню випадкового вгадування у збалансованому наборі даних. Збалансована точність може слугувати загальною метрикою продуктивності моделі, незалежно від того, чи є справжні мітки в даних незбалансованими, чи ні, вважаючи втрати на ХН такими же, як і на ХП.
Іншою метрикою є рівень позитивного прогнозованого стану (РППС, англ. predicted positive condition rate, PPCR), що визначає відсоток від загальної сукупності, який буде промарковано. Наприклад, для пошукового рушія, що повертає 30 результатів (знайдених документів) з 1 000 000 документів, РППС становить 0,003 %.
- Рівень позитивного прогнозованого стану = ІП + ХПІП + ХП + ІН + ХН
Згідно Сайто та Ремсмаєра, при оцінюванні бінарних класифікаторів на незбалансованих даних графіки влучності—повноти є інформативнішими за графіки РХП. За таких сценаріїв графіки РХП можуть бути візуально оманливими для висновків про надійність виконання класифікації.[18]
Імовірнісна інтерпретація
Влучність і повноту також можливо інтерпретувати не як відношення, а як оцінки ймовірностей:[19]
- Влучність є оцінкою ймовірності того, що документ, випадково вибраний з пулу знайдених документів, є релевантним.
- Повнота є оцінкою ймовірності того, що документ, випадково вибраний з пулу релевантних документів, буде знайдено.
Іншою інтерпретацією є те, що влучність є усередненою ймовірністю релевантного знаходження, а повнота є усередненою ймовірністю повного знаходження, усереднені над багатократними запитами пошуку.
F-міра
Мірою, яка поєднує влучність та повноту, є середнє гармонійне влучності та повноти, традиційна F-міра, або збалансована F-оцінка:
- F = 2 · влучність · повнотавлучність + повнота
Ця міра є приблизно усередненням цих двох, коли вони є близькими, а загальніше є середнім гармонійним, що, у випадку двох чисел, збігається з квадратом середнього геометричного, поділеним на середнє арифметичне. Існує декілька причин, через які F-оцінку може бути критиковано за певних обставин через її зсув як оцінної метрики.[4] Вона є також відомою як міра F1, оскільки повнота та чутливість є зваженими рівномірно.
Вона є окремим випадком загальної міри Fβ (для невід'ємних дійсних значень β):
- Fβ = (1 + β2) · влучність · повнотаβ2 · влучність + повнота
Двома іншими широко вживаними мірами F є міра F2, яка приділяє повноті більшої ваги, аніж влучності, та міра F0,5, що робить більший акцент на влучності, аніж на повноті.
F-міру було виведено ван Рійсберґеном (1979) таким чином, що Fβ «вимірює ефективність пошуку з урахуванням користувача, який надає в β разів вищої важливості повноті, ніж влучності». Вона ґрунтується на мірі ефективності ван Рійсберґена Eα = 1 − 1αВ + 1−αП, де другий член є зваженим середнім гармонійним влучності та повноти з вагами (α, 1 − α). Вони є взаємопов'язаними як Fβ = 1 − Eα, де α = 11 + β2.
Обмеження як цілі
Існують інші параметри та стратегії міри продуктивності системи інформаційного пошуку, такі як площа під кривою РХП (ППК, англ. AUC).[20]
Див. також
- Коефіцієнт невизначеності, відомий також як вправність (англ. proficiency)
- Чутливість та специфічність
Джерела
- Гущин, І. В.; Сич, Д. О. (жовтень 2018). Аналіз впливу попередньої обробки тексту на результати текстової класифікації. Молодий вчений (Харківський національний університет імені В.Н. Каразіна) 10 (62): 264–266.
- Швець У. С. Основні поняття доказової медицини. — 2015.
- Коваль, С.С.; Макеєв, С.С.; Новікова, Т.Г. (2016). Оцінка ефективності застосування методики інтеграції даних ОФЕКТ/МРТ у діагностиці метастазів головного мозку. Клінічна онкологія (Київ: ДУ «Інститут нейрохірургії ім. акад. А.П. Ромоданова НАМН України») 3 (23).
- Powers, David M W (2011). Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation. Journal of Machine Learning Technologies 2 (1): 37–63. Архів оригіналу за 14 листопада 2019. (англ.)
- Perruchet, P.; Peereman, R. (2004). The exploitation of distributional information in syllable processing. J. Neurolinguistics 17 (2–3): 97–119. doi:10.1016/s0911-6044(03)00059-9. Проігноровано невідомий параметр
|s2cid=(довідка) (англ.) - Powers, David M. W. (2012). The Problem with Kappa. Conference of the European Chapter of the Association for Computational Linguistics (EACL2012) Joint ROBUS-UNSUP Workshop. (англ.)
-
- Kent, Allen; Berry, Madeline M.; Luehrs, Jr., Fred U.; Perry, J.W. (1955). Machine literature searching VIII. Operational criteria for designing information retrieval systems. American Documentation 6 (2): 93. doi:10.1002/asi.5090060209. (англ.)
- Смоляр, В.А.; Шаповал, Н.А.; Гузь, О.А; Хоперія, В.Г. (2013). Оцінка ефективності експрес-гістологічного дослідження у визначенні обсягу дисекції за папілярного раку щитоподібної залози. Клінічна ендокринологія та ендокринна хірургія (Київ: Український науково-практичний центр ендокринної хірургії, трансплантації ендокринних органів і тканин МОЗ України) 3 (44).
- Мірошниченко, І. В.; Івлієва, К. Г. (2019). Оцінювання кредитного ризику методами машинного навчання. doi:10.32702/2307-2105-2019.12.87.
- Fawcett, Tom (2006). An Introduction to ROC Analysis. Pattern Recognition Letters 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010. (англ.)
- Powers, David M W (2011). Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation. Journal of Machine Learning Technologies 2 (1): 37–63. (англ.)
- Ting, Kai Ming (2011). У Sammut, Claude; Webb, Geoffrey I. Encyclopedia of machine learning. Springer. ISBN 978-0-387-30164-8. doi:10.1007/978-0-387-30164-8. (англ.)
- Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (26 січня 2015). WWRP/WGNE Joint Working Group on Forecast Verification Research. Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Процитовано 17 липня 2019. (англ.)
- The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genomics 21 (1): 6-1–6-13. January 2020. PMC 6941312. PMID 31898477. doi:10.1186/s12864-019-6413-7. Проігноровано невідомий параметр
|vauthors=(довідка) (англ.) - Classification assessment methods. Applied Computing and Informatics. August 2018. doi:10.1016/j.aci.2018.08.003. Проігноровано невідомий параметр
|vauthors=(довідка); Проігноровано невідомий параметр|doi-access=(довідка) (англ.) - Olson, David L.; and Delen, Dursun (2008); Advanced Data Mining Techniques, Springer, 1st edition (February 1, 2008), page 138, ISBN 3-540-76916-1 (англ.)
- Mower, Jeffrey P. (12 квітня 2005). PREP-Mt: predictive RNA editor for plant mitochondrial genes. BMC Bioinformatics 6: 96. ISSN 1471-2105. PMC 1087475. PMID 15826309. doi:10.1186/1471-2105-6-96. (англ.)
- Saito, Takaya; Rehmsmeier, Marc (4 березня 2015). The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. У Brock, Guy. PLOS ONE (англ.) 10 (3): e0118432. Bibcode:2015PLoSO..1018432S. ISSN 1932-6203. PMC 4349800. PMID 25738806. doi:10.1371/journal.pone.0118432. Проігноровано невідомий параметр
|lay-url=(довідка); Проігноровано невідомий параметр|lay-date=(довідка) (англ.) - Fatih Cakir, Kun He, Xide Xia, Brian Kulis, Stan Sclaroff, Deep Metric Learning to Rank, In Proc. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2019. (англ.)
- Zygmunt Zając. What you wanted to know about AUC. http://fastml.com/what-you-wanted-to-know-about-auc/ (англ.)
- Baeza-Yates, Ricardo; Ribeiro-Neto, Berthier (1999). Modern Information Retrieval. New York, NY: ACM Press, Addison-Wesley, Seiten 75 ff. ISBN 0-201-39829-X (англ.)
- Hjørland, Birger (2010); The foundation of the concept of relevance, Journal of the American Society for Information Science and Technology, 61(2), 217—237 (англ.)
- Makhoul, John; Kubala, Francis; Schwartz, Richard; and Weischedel, Ralph (1999); Performance measures for information extraction, in Proceedings of DARPA Broadcast News Workshop, Herndon, VA, February 1999 (англ.)
- van Rijsbergen, Cornelis Joost «Keith» (1979); Information Retrieval, London, GB; Boston, MA: Butterworth, 2nd Edition, ISBN 0-408-70929-4 (англ.)