Гіпербола Кіперта

Гіпербола Кіперта — крива, ізогонально спряжена прямій, що проходить через точку Лемуана і центр описаного кола даного трикутника.

• Пряма, що проходить через центр описаного кола і точку Лемуана, називається віссю Брокара. На ній лежать точки Аполлонія. Інакше кажучи, гіпербола Кіперта — крива, ізогонально спряжена осі Брокара даного трикутника.

Точка на гіперболі Кіперта.

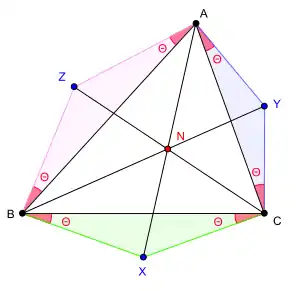
Визначення через трикутники в трикутних координатах[1]:

Якщо три трикутники ${\displaystyle XBC}$, ${\displaystyle YCA}$ і ${\displaystyle ZAB}$ побудовані на сторонах трикутника ${\displaystyle ABC}$, є подібними, рівнобедреними з основами на сторонах початкового трикутника, і однаково розташованими (тобто всі вони побудовані або з зовнішнього боку, або з внутрішнього), то прямі ${\displaystyle AX}$, ${\displaystyle BY}$ і ${\displaystyle CZ}$ перетинаються в одній точці ${\displaystyle N}$. Тоді гіперболу Кіперта можна визначити, як геометричне місце точок ${\displaystyle N}$ (див. мал.).

Якщо спільний кут при основі дорівнює ${\displaystyle \theta }$, то вершини трьох трикутників мають такі трикутні координати:

• ${\displaystyle X(-\sin \theta$ :\sin(C+\theta ):\sin(B+\theta ))}
• ${\displaystyle Y(\sin(C+\theta ):-\sin \theta$ :\sin(A+\theta ))}
• ${\displaystyle Z(\sin(B+\theta ):\sin(A+\theta ):-\sin \theta )}$

${\displaystyle (\operatorname {cosec} (A+\theta ):\operatorname {cosec} (B+\theta ):\operatorname {cosec} (C+\theta ))}$.

Геометричне місце точок ${\displaystyle N}$ при зміненні кута при основі трикутників ${\displaystyle \theta }$ між ${\displaystyle -\pi /2}$ і ${\displaystyle \pi /2}$ є гіперболою Кіперта з рівнянням

${\displaystyle {\frac {\sin(B-C)}{x}}+{\frac {\sin(C-A)}{y}}+{\frac {\sin(A-B)}{z}}=0}$,

де ${\displaystyle x}$, ${\displaystyle y}$, ${\displaystyle z}$ — трилінійні координати точки ${\displaystyle N}$ у трикутнику.

Серед точок, що лежать на гіперболі Кіперта, є такі важливі точки трикутника[2]:

Значення ${\displaystyle \theta }$	Точка ${\displaystyle N}$
${\displaystyle 0}$	${\displaystyle G}$, центроїд трикутника ${\displaystyle ABC}$ (X2)
${\displaystyle \pi /2}$ (або ${\displaystyle -\pi /2}$)	${\displaystyle O}$, ортоцентр трикутника ${\displaystyle ABC}$ (X4)
${\displaystyle \operatorname {arctg} [\operatorname {tg} (A/2)\operatorname {tg} (B/2)\operatorname {tg} (C/2)]}$[3]	Центр Шпікера (X10)
${\displaystyle \pi /4}$	Зовнішня точка Вектена (X485)
${\displaystyle -\pi /4}$	Внутрішня точка Вектена (X486)
${\displaystyle \pi /6}$	${\displaystyle N_{1}}$, перша точка Наполеона (X17)
${\displaystyle -\pi /6}$	${\displaystyle N_{2}}$, друга точка Наполеона (X18)
${\displaystyle \pi /3}$	${\displaystyle F_{1}}$, перша точка Ферма (X13)
${\displaystyle -\pi /3}$	${\displaystyle F_{2}}$, Друга точка Ферма (X14)
${\displaystyle -A}$ (якщо ${\displaystyle A<\pi /2}$) ${\displaystyle \pi -A}$ (якщо ${\displaystyle A>\pi /2}$)	вершина ${\displaystyle A}$
${\displaystyle -B}$ (якщо ${\displaystyle B<\pi /2}$) ${\displaystyle \pi -B}$ (якщо ${\displaystyle B>\pi /2}$)	вершина ${\displaystyle B}$
${\displaystyle -C}$ (якщо ${\displaystyle C<\pi /2}$) ${\displaystyle \pi -C}$ (якщо ${\displaystyle C>\pi /2}$)	вершина ${\displaystyle C}$

Гіпербола Кіперта проходить через такі центри трикутника X(i):

• i=2, (центроїд трикутника),
• i=4 (ортоцентр),
• i=10 (центр Шпікера; тобто, інцентр трикутника з вершинами в серединах сторін даного трикутника ABC[1]),
• i=13 (перша точка Ферма), i = 14 (друга точка Ферма),
• i=17 (перша точка Наполеона), i = 18 (друга точка Наполеона),
• i=76 (третя точка Брокара),
• i=83 (точка, ізогонально спряжена серединній точці між точками Брокара[1]),
• i=94, 96,
• i=98 (точка Таррі),
• i=226, 262, 275, 321,
• i=485 (зовнішня точка Вектена), i = 486 (внутрішня точка Вектена),
• i = 598, 671, 801, 1029, 1131, 1132,
• i = 1139 (внутрішня точка п'ятикутника, англ. inner pentagon point), i = 1140 (зовнішня точка п'ятикутника, англ. outer pentagon point),
• i = 1327, 1328, 1446, 1676, 1677, 1751, 1916, 2009, 2010, 2051, 2052, 2394, 2592, 2593,
• i = 2671 (перша точка золотого арбелоса, англ. first golden arbelos point),
• i = 2672 (друга точка золотого арбелоса, англ. second golden arbelos point),
• i = 2986, 2996

Теорема Б. Гіберта (2000) узагальнює теорему про коло Лестер, а саме: будь-яке окружність, діаметр якого є хордою гіперболи Кіперта трикутника і перпендикулярний до його прямої Ейлера, проходить через точки Ферма[4][5].

Назву ця гіпербола отримала на честь німецького математика Фрідріха Вільгельма Августа Людвіга Кіперта (1846—1934), який відкрив її.[1]

• Гіпербола Кіперта — рівностороння або рівнобічна (тобто її асимптоти перпендикулярні), отже, її центр, позначений в енциклопедії центрів трикутника як Х (115), лежить на колі Ейлера.

• Трикутник
• Парабола Кіперта

• Eddy R. H., Fritsch R. . The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle // Math Magazine, 1994, 67. — P. 188—205.