Точки Аполлонія
Точки Аполлонія (іноді ізодинамічні центри[1]) — дві такі точки, відстані від яких до вершин трикутника обернено пропорційні сторонам, протилежним до цих вершин.
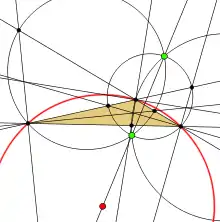
Точки Аполлонія виділено зеленим
Властивості
- Точки Аполлонія це центри інверсії, які перетворять даний трикутник у рівносторонній трикутник.
- Кола, побудовані як на діаметрі на відрізку, що з'єднує основи внутрішньої і зовнішньої бісектрис, випущених з одного кута, проходять через точки Аполлонія.
- Точки Аполлонія лежать на прямій, що з'єднує центр описаного кола з точкою Лемуана. Ця пряма називається віссю Брокара.
- Подерні трикутники точок Аполлонія правильні (іноді цю властивість приймають як визначення).
- Попередню властивість можна сформулювати інакше: три ортогональні проєкції точок Аполлонія на сторони даного трикутника є вершинами правильного трикутника.
- Точки Аполлонія ізогонально спряжені точкам Торрічеллі.
- Побудуємо дві прямі, кожна з яких проходить через точку Аполлонія і точку Торрічеллі, відмінну від ізогонально спряженої їй. Такі прямі перетнуться в точці перетину медіан (у центроїді трикутника).
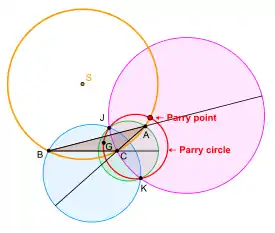
Коло і точка Паррі. (G — центроїд, а J і K — точки Аполлонія трикутника ABC)
- Нехай ABC — трикутник на площині. Коло, що проходить через центроїд і дві точки Аполлонія трикутника ABC, називають колом Паррі трикутника ABC (на малюнку праворуч воно червоне). Воно також проходить через точку Паррі (червона точка в чорному кільці).
- Розглянемо три сфери, що дотикаються до площини в точках і одна з одною зовнішнім чином. Якщо радіуси цих сфер рівні , то і т. д. Тому дві сфери, що дотикаються до трьох даних і площини, дотикатимуться до площини в точках Аполлонія.
- Кубика Нейберга - множина таких точок , що — прямої Ейлера (зафіксовано її нескінченно віддалену точку). На цій кубиці лежить більше 15 чудових точок, зокрема, точки Торрічеллі, Аполлонія, ортоцентр, центр описаного кола, вершини правильних трикутників, побудованих на сторонах (зовнішньо або внутрішньо), точки, симетричні вершинам відносно сторін, дві точки Ферма, дві ізодинамічні точки, нескінченна точка Ейлера, а також центри вписаного і зовнівписаного кіл, що лежать на всіх кубиках. У списку кубик плоского трикутника Берхарта Гіберта кубика Нейберга зазначена як K001[2].
Див. також
Примітка
- Katarzyna Wilczek. The harmonic center of a trilateral and the Apollonius point of a triangle // Journal of Mathematics and Applications : journal. — 2010. — Vol. 32 (23 January). — P. 95—101.
- K001 at Berhard Gibert's Cubics in the Triangle Plane// Архівовано серпень 20, 2009 на сайті Wayback Machine.
Посилання
- Moon, Tarik Adnan (2010). The Apollonian circles and isodynamic points. Mathematical Reflections (6). Архів оригіналу за 20 квітня 2013.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
