Лінія Ейлера
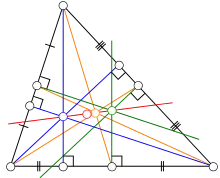
В геометрії пряма Ейлера, названа на честь Леонарда Ейлера, — це пряма, яка визначена для будь-якого трикутника відмінного від рівностороннього. Вона є центральною прямою трикутника і проходить через кілька важливих точок, які визначаються по трикутнику, включаючи ортоцентр, описане коло, центроїд, точку Ексетера та центр кола дев'яти точок трикутника[1].
Поняття прямої Ейлера в трикутнику поширюється на пряму Ейлера для інших фігур, такі як чотирикутник і тетраедр.
Центри трикутника на прямій Ейлера
Окремі центри
У 1765 році Ейлер показав, що в будь-якому трикутнику ортоцентр, центр описаного кола та центроїд лежать на одній прямій[2]. Ця властивість справедлива і для іншого центра трикутника, — центра кола дев'яти точок, хоча він не був визначений за часів Ейлера. У рівносторонніх трикутниках ці чотири точки збігаються, але в будь-якому іншому трикутнику всі вони відрізняються один від одного, і пряма Ейлера визначається будь-якими двома з них.
Інші визначні точки, які лежать на прямій Ейлера, включають точку Лонгшампа, точку Шифлера, точку Ексетера та перспектор Госсара[1]. Однак центр вписаного кола, зазвичай, не лежить на прямій Ейлера[3]; він знаходиться на прямій Ейлера лише для рівнобедрених трикутників[4], для якої пряма Ейлера збігається з віссю симетрії трикутника і містить усі центри трикутника.
Тангенціальний трикутник опорного трикутника дотичний до кола описаного навколо останнього у вершинах опорного трикутника. Цент кола описаного навколо дотичного трикутника лежить на прямій Ейлера опорного трикутника[5][6]. Центр подібності ортичного трикутника (утвореного основами висот) та дотичного трикутника також знаходиться на прямій Ейлера[5][6].
Векторне доведення
Розглянемо трикутник . Довести, що центр описаного кола , центроїд та ортоцентр є колінеарними, можна за допомогою векторів. По-перше, задовольняє відношенню:
Це випливає з того, що модулі барицентричних координат відносяться як . Далі, задача Сильвестра[7] інтерпретується як
Тепер, за допомогою векторного додавання, отримаємо, що
Додаючи усі ці три вирази, отримаємо, що
Остаточно, і три точки , і (у такій послідовності) будуть колінеарними.
У книзі Доррі[7] пряма Ейлера та проблема Сильвестра об'єднані в одне доведення. Однак більшість доказів задачі Сильвестра спираються на основні властивості вільних векторів, незалежно від прямої Ейлера.
Відстані між центрами
На прямій Ейлера центроїд знаходиться між центром описаного кола і ортоцентром , і вдвічі далі від ортоцентра, ніж від центра описаного кола[6]:
Відрізок — це діаметр ортоцентроїдального кола.
Центр кола дев'яти точок лежить уздовж прямої Ейлера посередині між ортоцентром і центром описаного кола[1]:
Таким чином, пряма Ейлера може бути представлена на числовій прямій з центром описаного кола розташованим у 0, центроїдом в 2, центром кола дев'яти точок у 3 і ортоцентрі в 6, для деякого коефіцієнту масштабу . Крім того, квадрат відстані між центроїдом та центром описаного кола на прямій Ейлера менше, ніж R2 описаного кола на величину, яка дорівнює 1/9 сумі квадратів сторін трикутника , та [6]:
Також виконуються[6],
Представлення
Нехай A, B, C позначають кути вершин трикутника, x : y : z — задають координати точки у трилінійних координатах; тоді рівнянням прямої Ейлера буде
Рівняння для прямої Ейлера в барицентричних координатах [8]:
Параметричне представлення
Інший спосіб представити пряму Ейлера — залежною від параметра t. Скористаємось трилінійними координатами двох точок — центром описаного кола (з трилінійними координатами ) та ортоцентром (з трилінійними координатами . Тоді кожна точка на прямій Ейлера, крім ортоцентра, задається трилінійними координатами
як лінійна комбінація трилінійними координат цих двох точок, для деякого t.
Наприклад:
- Центр описаного кола має трилінійні координати , що відповідає значенню параметра
- Центроїд має трилінійні координати , що відповідає значенню параметра
- Центр кола дев'яти точок має трилінійні координати , що відповідає значенню параметра
- Точка Лонгшампа має трилінійні координати , що відповідає значенню параметра
Нахил
У декартовій системі координат позначають нахили сторін трикутника як та і позначають нахил його прямої Ейлера як . Тоді вони пов'язані рівнянням[9]
Таким чином, нахил прямої Ейлера (якщо він скінченний) виражається в термінах нахилів сторін як
Більше того, пряма Ейлера паралельна стороні гострого трикутника BC тоді і лише тоді, коли[9]
Зв'язок з вписаними рівносторонніми трикутниками
Геометричне місце точок центроїдів рівносторонніх трикутників, вписаних у даний трикутник, утворена двома прямими, перпендикулярними прямій Ейлера даного трикутника[10].
У спеціальних трикутниках
Прямокутний трикутник
У прямокутному трикутнику пряма Ейлера збігається з медіаною проведеною до гіпотенузи, тобто вона проходить через вершину прямого кута і через середину сторони, протилежну цій вершині. Це тому, що ортоцентр прямокутного трикутника, перетин його висот потрапляє у вершину прямого кута, тоді як його центр описаного кола, перетин серединних перпендикулярів до сторін, потрапляє на середину гіпотенузи.
Рівнобедрений трикутник
Пряма Ейлера в рівнобедреному трикутнику збігається з віссю симетрії. У рівнобедреному трикутнику центр вписаного кола потрапляє на лінію Ейлера.
Примітки
- Kimberling, Clark (1998). Triangle centers and central triangles. Congressus Numerantium 129: i–xxv, 1–295.
- Euler, Leonhard (1767). Solutio facilis problematum quorundam geometricorum difficillimorum [Easy solution of some difficult geometric problems]. Novi Commentarii Academiae Scientarum Imperialis Petropolitanae 11: 103–123. E325. Reprinted in Opera Omnia, ser. I, vol. XXVI, pp. 139–157, Societas Scientiarum Naturalium Helveticae, Lausanne, 1953, MR0061061. Summarized at: Dartmouth College.
- Schattschneider, Doris; King, James (1997). Geometry Turned On: Dynamic Software in Learning, Teaching, and Research. The Mathematical Association of America. с. 3–4. ISBN 978-0883850992.
- Edmonds, Allan L.; Hajja, Mowaffaq; Martini, Horst (2008). Orthocentric simplices and biregularity. Results in Mathematics 52 (1–2): 41–50. MR 2430410. doi:10.1007/s00025-008-0294-4. «It is well known that the incenter of a Euclidean triangle lies on its Euler line connecting the centroid and the circumcenter if and only if the triangle is isosceles».
- Leversha, Gerry; Smith, G. C. (November 2007). Euler and triangle geometry. The Mathematical Gazette 91 (522): 436–452. JSTOR 40378417..
- Altshiller-Court, Nathan, College Geometry, Dover Publications, 2007 (orig. Barnes & Noble 1952).
- Dörrie, Heinrich, «100 Great Problems of Elementary Mathematics. Their History and Solution». Dover Publications, Inc., New York, 1965, ISBN 0-486-61348-8, pages 141 (Euler's Straight Line) and 142 (Problem of Sylvester)
- Scott, J.A., «Some examples of the use of areal coordinates in triangle geometry», Mathematical Gazette 83, November 1999, 472—477.
- Wladimir G. Boskoff, Laurent¸iu Homentcovschi, and Bogdan D. Suceava, «Gossard's Perspector and Projective Consequences», Forum Geometricorum, Volume 13 (2013), 169—184.
- Francisco Javier Garc ́ıa Capita ́n, «Locus of Centroids of Similar Inscribed Triangles», Forum Geometricorum 16, 2016, 257—267 .http://forumgeom.fau.edu/FG2016volume16/FG201631.pdf
Посилання
- An interactive applet showing several triangle centers that lies on the Euler line.(англ.)
- "Euler Line" and "Non-Euclidean Triangle Continuum" at the Wolfram Demonstrations Project
- Nine-point conic and Euler line generalization, A further Euler line generalization, and The quasi-Euler line of a quadrilateral and a hexagon at Dynamic Geometry Sketches
- Олександр Богомольний, Висота трикутника та пряма Ейлера та Пряма Ейлера та коло 9-ти точок на сайті «cut-the-knot»
- Kimberling, Clark. Triangle centers on the Euler line. Triangle Centers.
- Stankova, Zvezdelina (1 лютого 2016). Triangles have a Magic Highway. Numberphile (YouTube).
- Weisstein, Eric W. Euler Line(англ.) на сайті Wolfram MathWorld.
