Гіперболоїд
Гіперболо́їд (грец. hyperbole — гіпербола, і грец. eidos — подібність) — вид поверхні другого порядку в тривимірному просторі, що задається в Декартових координатах рівнянням
- (Однопорожнинний гіперболоїд), де a і b — дійсні півосі, а c — уявна піввісь;
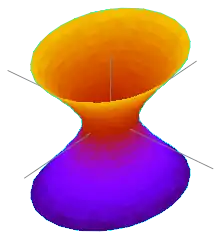
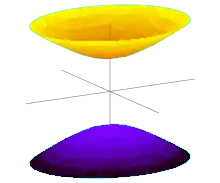
або
- (двопорожнинний гіперболоїд), де a і b — уявні півосі, а c — дійсна піввісь.
Якщо a = b, то така поверхня зветься — гіперболоїд обертання. Однопорожнинний гіперболоїд обертання можна отримати обертанням гіперболи навколо її уявної осі, двопорожнинний — навколо дійсної. Двопорожнинний гіперболоїд обертання також є геометричним місцем точок P, модуль різниці відстаней від яких до двох заданих точок A і B є сталим: . У такому випадку точки A і B звуться фокусами Гіперболоїда.
Однопорожнинний гіперболоїд є двічі лінійчатою поверхнею. Якщо він є гіперболоїдом обертання, то його можна отримати обертанням прямої навколо іншої прямої, що є мимобіжною з нею. Цю властивість лінійчатих однопорожнинних гіперболоїдів використовують в архітектурі. Зокрема, вежа Шухова в Москві є гіперболоїдною конструкцією. Вона складена саме з гіперболоїдів, що утворені прямими стрижнями.
Більш, ніж у трьох вимірах
Уявні гіперболоїди — звичне явище в математиці високих розмірностей. Наприклад, у псевдо-Евклідовому просторі розглянемо квадратичну форму:
Якщо c є довільною сталою, то частина простору, в межах
називається гіперболоїдом. Випадок, коли c = 0 є виродженим.
Кривина та тензор Річчі гіперболоїда
Геометрію гіперболоїда можна просто описати, представивши його вкладеним в фіктивний чотиривимірний простір:
- .
Введенням координат
можна задовольнити , а елементи довжин на поверхні матимуть вигляд (елементарно перевіряється підстановкою)
.
Як видно, метричний тензор має специфічну структуру: є діагональним, перший діагональний елемент рівен одиниці, другий залежить від першої змінної, третій — від першої і другої, а від третьої змінної залежності немає, що, деякою мірою, відповідає ізотропії простору.
Виходячи із цього, можна визначити вирази для символів Кристоффеля: маючи загальний вираз
,
де метричний тензор має вигляд
,
для частинних випадків виразів можна отримати
;
;
оскільки, в силу структури метричних тензорів, ;
;
.
Тепер можна спростити (якомога більше зменшити кількість сум) вираз для тензора Річчі: маючи загальне визначення,
,
та вирази ,
для тензора можна отримати (сума лише по індексах )
.
Справді, використовуючи вирази , для доданків можна отримати наступні вирази.
Перший доданок:
.
Другий доданок залишається без змін.
Третій доданок:
.
Четвертий доданок:
.
Для двох останніх доданків доведеться повторити цю ж саму процедуру:
,
.
Отже,
.
Додавши вирази для всіх доданків та замінивши німий індекс на , можна отримати .
Тепер можна застосувати спрощений вигляд для тензора Річчі до метрики описаних вище просторів. Наприклад, можна взяти гіперболічний простір. Треба обчислити компоненти . Спочатку доведеться отримати, користуючись , явний вигляд для символів Кристоффеля:
,
,
,
,
,
.
Тоді, наприклад, компонента 11 тензора, із урахуванням цих виразів та , має вираз
.
Компонента 22:
.
Компонента 33:
.
Аналогічні викладки (перевіряються повністю ідентично попереднім) дають
.
Отже, для гіперболоїда
.
Згортаючи тензор Річчі із метричним тензором (відповідно до визначення скалярної кривини), можна отримати, що для гіперболоїда скалярна кривина рівна
.
Отже, гіперболічний простір — простір з постійною скалярною кривиною.
У мистецтві
В архітектурі
Лінійчата конструкція, що має форму однополостного гіперболоїда, є жорсткої: якщо балки з'єднати шарнірно, гіперболоїдна конструкція все одно буде зберігати свою форму під дією зовнішніх сил.
Для високих споруд основну небезпеку несе вітрове навантаження, а у ґратчастої конструкції вона невелика. Ці особливості роблять гіперболоїдні конструкції міцними, незважаючи на невисоку матеріаломісткість.
Прикладами гіперболоїдних конструкцій є:
У літературі
- Гіперболоїд інженера Гаріна (хоча насправді це мав бути параболоїд)
Див. також
- Параболоїд — інший вид поверхні другого порядку
- Гіперболічний параболоїд
- Гіперболоїдні конструкції
Посилання
- Гіперболоїди // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 157. — 594 с.
- http://mathworld.wolfram.com/Hyperboloid.html
