Добуток Хатрі-Рао

Добуток Хатрі-Рао (англ. Khatri-Rao product) — матрична операція перемноження матриць, що визначається виразом[1][2]:

\mathbf {A} \ast \mathbf {B} =\left(\mathbf {A} _{ij}\otimes \mathbf {B} _{ij}\right)_{ij}

в якому ij-й блок являє собою добуток Кронекера m_ip_i × n_jq_j відповідних блоків A і B за умови, що кількість рядків і стовпців обох матриць однакова. Розмірність добутку — (Σ_i m_ip_i) × (Σ_j n_jq_j).

Наприклад, якщо матриці A і B мають блокову розмірність 2 × 2

\mathbf {A} =\left[{\begin{array}{c | c}\mathbf {A} _{11}&\mathbf {A} _{12}\\\hline \mathbf {A} _{21}&\mathbf {A} _{22}\end{array}}\right]=\left[{\begin{array}{c c | c}1&2&3\\4&5&6\\\hline 7&8&9\end{array}}\right],\quad \mathbf {B} =\left[{\begin{array}{c | c}\mathbf {B} _{11}&\mathbf {B} _{12}\\\hline \mathbf {B} _{21}&\mathbf {B} _{22}\end{array}}\right]=\left[{\begin{array}{c | c c}1&4&7\\\hline 2&5&8\\3&6&9\end{array}}\right],

отримаємо:

\mathbf {A} \ast \mathbf {B} =\left[{\begin{array}{c | c}\mathbf {A} _{11}\otimes \mathbf {B} _{11}&\mathbf {A} _{12}\otimes \mathbf {B} _{12}\\\hline \mathbf {A} _{21}\otimes \mathbf {B} _{21}&\mathbf {A} _{22}\otimes \mathbf {B} _{22}\end{array}}\right]=\left[{\begin{array}{c c | c c}1&2&12&21\\4&5&24&42\\\hline 14&16&45&72\\21&24&54&81\end{array}}\right].

Стовпцевий добуток Хатрі-Рао

Стовпцевий добуток Кронекера двох матриць також прийнято називати добутком Хатрі-Рао. Цей добуток передбачає, що блоки матриць є їх стовпцями. В такому випадку m₁ = m, p₁ = p, n = q і для кожного j: n_j = p_j = 1. Результатом добутку є mp × n- матрица, кожен стовпець якої отримується як добуток Кронекера відповідних стовпців матриць A і B. Спираючись на розбитття матриць з попереднього прикладу на стовпці, отримаємо:

\mathbf {C} =\left[{\begin{array}{c | c | c}\mathbf {C} _{1}&\mathbf {C} _{2}&\mathbf {C} _{3}\end{array}}\right]=\left[{\begin{array}{c | c | c}1&2&3\\4&5&6\\7&8&9\end{array}}\right],\quad \mathbf {D} =\left[{\begin{array}{c | c | c }\mathbf {D} _{1}&\mathbf {D} _{2}&\mathbf {D} _{3}\end{array}}\right]=\left[{\begin{array}{c | c | c }1&4&7\\2&5&8\\3&6&9\end{array}}\right],

і далі:

\mathbf {C} \ast \mathbf {D} =\left[{\begin{array}{c | c | c }\mathbf {C} _{1}\otimes \mathbf {D} _{1}&\mathbf {C} _{2}\otimes \mathbf {D} _{2}&\mathbf {C} _{3}\otimes \mathbf {D} _{3}\end{array}}\right]=\left[{\begin{array}{c | c | c }1&8&21\\2&10&24\\3&12&27\\4&20&42\\8&25&48\\12&30&54\\7&32&63\\14&40&72\\21&48&81\end{array}}\right].

Застосування

Стовпцева версія добутку Хатрі-Рао застосовується в лінійній алгебрі для аналітичної обробки даних[3] і оптимізації рішень проблеми обернення діагональних матриць.[4][5]

В 1996 р. стовпцевий добуток Хатрі-Рао був запропонований для формалізації задачі оцінювання напрямку приходу та часу затримки сигналів в цифровій антенній решітці[6], а також для опису відгуку 4-координатного радара[7].

Торцевий добуток

Торцевий добуток матриць

Альтернативна концепція добутку матриць, яка на відміну від стовпцевої версії добутку Хатрі-Рао використовує розбиття матриць на рядки, була запропонована Слюсарем В. І.[8] в 1996 р. і названа ним торцевий добуток (англ. face-splitting product)[7][9][10][11] або транспонований добуток Хатрі-Рао (англ. transposed Khatri-Rao product)[12].

Цей тип матричного добутку спирається на перемноження елементів рядків двох і більше матриць з однаковою кількістю рядків за правилом добутку Кронекера. Використовуючи розбиття матриць з попередніх прикладів на рядки:

\mathbf {C} =\left[{\begin{array}{c c}\mathbf {C} _{1}\\\hline \mathbf {C} _{2}\\\hline \mathbf {C} _{3}\\\end{array}}\right]=\left[{\begin{array}{c  c  c}1&2&3\\\hline 4&5&6\\\hline 7&8&9\end{array}}\right],\quad \mathbf {D} =\left[{\begin{array}{c }\mathbf {D} _{1}\\\hline \mathbf {D} _{2}\\\hline \mathbf {D} _{3}\\\end{array}}\right]=\left[{\begin{array}{c  c  c }1&4&7\\\hline 2&5&8\\\hline 3&6&9\end{array}}\right],

можна записати[7][9][10]:

\mathbf {C} \bullet \mathbf {D} =\left[{\begin{array}{c }\mathbf {C} _{1}\otimes \mathbf {D} _{1}\\\hline \mathbf {C} _{2}\otimes \mathbf {D} _{2}\\\hline \mathbf {C} _{3}\otimes \mathbf {D} _{3}\\\end{array}}\right]=\left[{\begin{array}{c  c  c  c  c  c  c  c  c }1&4&7&2&8&14&3&12&21\\\hline 8&20&32&10&25&40&12&30&48\\\hline 21&42&63&24&48&72&27&54&81\end{array}}\right].

Основні властивості

Транспонування (Слюсар В.І., 1996[7][9][13]):
$\left(\mathbf {A} \bullet \mathbf {B} \right)^{\textsf {T}}={\textbf {A}}^{\textsf {T}}\ast \mathbf {B} ^{\textsf {T}}$
Комутативність і асоціативність[7][9][13]:
${\begin{aligned}\mathbf {A} \bullet (\mathbf {B} +\mathbf {C} )&=\mathbf {A} \bullet \mathbf {B} +\mathbf {A} \bullet \mathbf {C} ,\\(\mathbf {B} +\mathbf {C} )\bullet \mathbf {A} &=\mathbf {B} \bullet \mathbf {A} +\mathbf {C} \bullet \mathbf {A} ,\\(k\mathbf {A} )\bullet \mathbf {B} &=\mathbf {A} \bullet (k\mathbf {B} )=k(\mathbf {A} \bullet \mathbf {B} ),\\(\mathbf {A} \bullet \mathbf {B} )\bullet \mathbf {C} &=\mathbf {A} \bullet (\mathbf {B} \bullet \mathbf {C} ),\\\end{aligned}}$

де A, B і C — матриці, а k — скаляр,

$a\bullet \mathbf {B} =\mathbf {B} \bullet a$ ,[13]
де $a$ — вектор з тією ж кількістю елементів, що і кількість рядків матриці $\mathbf {B}$ ,
Властивість змішаного добутку (1997[13]):
$(\mathbf {A} \bullet \mathbf {B} )\left(\mathbf {A} ^{\textsf {T}}\ast \mathbf {B} ^{\textsf {T}}\right)=\left(\mathbf {A} \mathbf {A} ^{\textsf {T}}\right)\circ \left(\mathbf {B} \mathbf {B} ^{\textsf {T}}\right)$ ,

$(\mathbf {A} \bullet \mathbf {B} )(\mathbf {C} \ast \mathbf {D} )=(\mathbf {A} \mathbf {C} )\circ (\mathbf {B} \mathbf {D} )$ ,

$(\mathbf {A} \bullet \mathbf {B} \bullet \mathbf {C} \bullet \mathbf {D} )(\mathbf {L} \ast \mathbf {M} \ast \mathbf {N} \ast \mathbf {P} )=(\mathbf {A} \mathbf {L} )\circ (\mathbf {B} \mathbf {M} )\circ (\mathbf {C} \mathbf {N} )\circ (\mathbf {D} \mathbf {P} )$ [12],

$(\mathbf {A} \ast \mathbf {B} )^{\textsf {T}}(\mathbf {A} \ast \mathbf {B} )=(\mathbf {A} ^{\textsf {T}}\mathbf {A} )\circ (\mathbf {B} ^{\textsf {T}}\mathbf {B} )$ [14],
де $\circ$ означає добуток Адамара,
$(\mathbf {A} \circ \mathbf {B} )\bullet (\mathbf {C} \circ \mathbf {D} )=(\mathbf {A} \bullet \mathbf {C} )\circ (\mathbf {B} \bullet \mathbf {D} )$ [13],
$\mathbf {A} \otimes (\mathbf {B} \bullet \mathbf {C} )=(\mathbf {A} \otimes \mathbf {B} )\bullet \mathbf {C}$ [7],
$(\mathbf {A} \otimes \mathbf {B} )(\mathbf {C} \ast \mathbf {D} )=(\mathbf {A} \mathbf {C} )\ast (\mathbf {B} \mathbf {D} )$ [14],
$(\mathbf {A} \bullet \mathbf {B} )(\mathbf {C} \otimes \mathbf {D} )=(\mathbf {A} \mathbf {C} )\bullet (\mathbf {B} \mathbf {D} )$ [10][15],
$(\mathbf {A} \bullet \mathbf {L} )(\mathbf {B} \otimes \mathbf {M} )...(\mathbf {C} \otimes \mathbf {S} )=(\mathbf {A} \mathbf {B} ...\mathbf {C} )\bullet (\mathbf {L} \mathbf {M} ...\mathbf {S} )$ ,
$c^{\textsf {T}}\bullet d^{\textsf {T}}=c^{\textsf {T}}\otimes d^{\textsf {T}}$ [13],
$c\ast d=c\otimes d$ , де $c$ і $d$ є векторами узгодженої розмірності,
$(\mathbf {A} \ast c^{\textsf {T}})d=(\mathbf {A} \ast d^{\textsf {T}})c$ [16], $d^{\textsf {T}}(c\bullet \mathbf {A} ^{\textsf {T}})=c^{\textsf {T}}(d\bullet \mathbf {A} ^{\textsf {T}})$ ,
$(\mathbf {A} \bullet \mathbf {B} )(c\otimes d)=(\mathbf {A} c)\circ (\mathbf {B} d)$ [17], де $c$ і $d$ є векторами узгодженої розмірності,
$(\mathbf {A} \bullet \mathbf {B} )(\mathbf {M} \mathbf {N} c\otimes \mathbf {Q} \mathbf {P} d)=(\mathbf {A} \mathbf {M} \mathbf {N} c)\circ (\mathbf {B} \mathbf {Q} \mathbf {P} d)$ ,
${\mathcal {F}}(C^{(1)}x\star C^{(2)}y)=({\mathcal {F}}C^{(1)}\bullet {\mathcal {F}}C^{(2)})(x\otimes y)={\mathcal {F}}C^{(1)}x\circ {\mathcal {F}}C^{(2)}y$ ,
де $\star$ є символом векторної згортки, і ${\mathcal {F}}$ — матриця дискретного перетворення Фур'є (тотожність є розвитком властивості відлікового скетча[18]),
$\mathbf {A} \bullet \mathbf {B} =(\mathbf {A} \otimes \mathbf {1_{c}} ^{\textsf {T}})\circ (\mathbf {1_{k}} ^{\textsf {T}}\otimes \mathbf {B} )$ [19], де $\mathbf {A}$ — $r\times c$ матриця, $\mathbf {B}$ — $r\times k$ матриця, $\mathbf {1_{c}}$ , $\mathbf {1_{k}}$ — вектори з $c$ та $k$ одиниць відповідно,
$\mathbf {M} \bullet \mathbf {M} =(\mathbf {M} \otimes \mathbf {1} ^{\textsf {T}})\circ (\mathbf {1} ^{\textsf {T}}\otimes \mathbf {M} )$ [20], де $\mathbf {M}$ є $r\times c$ матрицею, $\circ$ — добуток Адамара і $\mathbf {1}$ — вектор з $c$ одиниць.
$\mathbf {M} \bullet \mathbf {M} =\mathbf {M} [\circ ](\mathbf {M} \otimes \mathbf {1} ^{\textsf {T}})$ , де $[\circ ]$ — символ проникаючого торцевого добутку матриць.
Аналогічно, $\mathbf {P} \ast \mathbf {N} =(\mathbf {P} \otimes \mathbf {1_{c}} )\circ (\mathbf {1_{k}} \otimes \mathbf {N} )$ , де $\mathbf {P}$ — $c\times r$ матриця, $\mathbf {N}$ — $k\times r$ матриця.
$\mathbf {W_{d}} \mathbf {A} =\mathbf {w} \bullet \mathbf {A}$ [13],
$vec(\mathbf {A} ^{\textsf {T}}\mathbf {W_{d}} \mathbf {A} )=(\mathbf {A} \bullet \mathbf {A} )^{\textsf {T}}\mathbf {w}$ [20], $vec(\mathbf {A} \mathbf {W_{d}} \mathbf {A} ^{\textsf {T}})=(\mathbf {A} ^{\textsf {T}}\bullet \mathbf {A} ^{\textsf {T}})^{\textsf {T}}\mathbf {w} =(\mathbf {A} \ast \mathbf {A} )\mathbf {w}$ ,
де $\mathbf {w}$ — вектор, утворений із діагональних елементів матриці $\mathbf {W_{d}}$ , $vec(\mathbf {A} )$ — операція формування вектора з матриці $\mathbf {A}$ шляхом розташування один під одним її стовпців.
Властивість поглинання добутку Кронекера:
$(\mathbf {A} \bullet \mathbf {L} )(\mathbf {B} \otimes \mathbf {M} )...(\mathbf {C} \otimes \mathbf {S} )(\mathbf {K} \ast \mathbf {T} )=(\mathbf {A} \mathbf {B} ...\mathbf {C} \mathbf {K} )\circ (\mathbf {L} \mathbf {M} ...\mathbf {S} \mathbf {T} )$ [10][15],
$(\mathbf {A} \bullet \mathbf {L} )(\mathbf {B} \otimes \mathbf {M} )...(\mathbf {C} \otimes \mathbf {S} )(c\otimes d)=(\mathbf {A} \mathbf {B} ...\mathbf {C} c)\circ (\mathbf {L} \mathbf {M} ...\mathbf {S} d)$ ,
$(\mathbf {A} \bullet \mathbf {L} )(\mathbf {B} \otimes \mathbf {M} )...(\mathbf {C} \otimes \mathbf {S} )(\mathbf {P} c\otimes \mathbf {Q} d)=(\mathbf {A} \mathbf {B} ...\mathbf {C} \mathbf {P} c)\circ (\mathbf {L} \mathbf {M} ...\mathbf {S} \mathbf {Q} d)$ ,
де $c$ і $d$ є векторами узгодженої розмірності,

Наприклад[17],
${\begin{aligned}\\&\quad \left({\begin{bmatrix}1&0\\0&1\\1&0\end{bmatrix}}\bullet {\begin{bmatrix}1&0\\1&0\\0&1\end{bmatrix}}\right)\left({\begin{bmatrix}1&1\\1&-1\end{bmatrix}}\otimes {\begin{bmatrix}1&1\\1&-1\end{bmatrix}}\right)\left({\begin{bmatrix}\sigma _{1}&0\\0&\sigma _{2}\\\end{bmatrix}}\otimes {\begin{bmatrix}\rho _{1}&0\\0&\rho _{2}\\\end{bmatrix}}\right)\left({\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}\ast {\begin{bmatrix}y_{1}\\y_{2}\end{bmatrix}}\right)\\[5pt]&\quad =\left({\begin{bmatrix}1&0\\0&1\\1&0\end{bmatrix}}\bullet {\begin{bmatrix}1&0\\1&0\\0&1\end{bmatrix}}\right)\left({\begin{bmatrix}1&1\\1&-1\end{bmatrix}}{\begin{bmatrix}\sigma _{1}&0\\0&\sigma _{2}\\\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}\,\otimes \,{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}{\begin{bmatrix}\rho _{1}&0\\0&\rho _{2}\\\end{bmatrix}}{\begin{bmatrix}y_{1}\\y_{2}\end{bmatrix}}\right)\\[5pt]&\quad ={\begin{bmatrix}1&0\\0&1\\1&0\end{bmatrix}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}{\begin{bmatrix}\sigma _{1}&0\\0&\sigma _{2}\\\end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\end{bmatrix}}\,\circ \,{\begin{bmatrix}1&0\\1&0\\0&1\end{bmatrix}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}{\begin{bmatrix}\rho _{1}&0\\0&\rho _{2}\\\end{bmatrix}}{\begin{bmatrix}y_{1}\\y_{2}\end{bmatrix}}\end{aligned}}$

та інші. Крім того, Слюсарем В. І. були запропоновані блокові версії транспонованого добутку та досліджені їх властивості[7].

Блоковий торцевий добуток

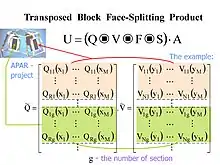
Застосування блокового транспонованого торцевого добутку для опису відгуку багатогранної цифрової антенної решітки[15]

Для блокових матриць з однаковою кількістю рядків у відповідних блоках

\mathbf {A} =\left[{\begin{array}{c | c}\mathbf {A} _{11}&\mathbf {A} _{12}\\\hline \mathbf {A} _{21}&\mathbf {A} _{22}\end{array}}\right],\quad \mathbf {B} =\left[{\begin{array}{c | c}\mathbf {B} _{11}&\mathbf {B} _{12}\\\hline \mathbf {B} _{21}&\mathbf {B} _{22}\end{array}}\right],

згідно з визначенням[7][10], блоковий торцевий добуток $\mathbf {A} [\bullet ]\mathbf {B}$ запишеться у вигляді:

\mathbf {A} [\bullet ]\mathbf {B} =\left[{\begin{array}{c | c}\mathbf {A} _{11}\bullet \mathbf {B} _{11}&\mathbf {A} _{12}\bullet \mathbf {B} _{12}\\\hline \mathbf {A} _{21}\bullet \mathbf {B} _{21}&\mathbf {A} _{22}\bullet \mathbf {B} _{22}\end{array}}\right]

.

Аналогічно для блокового транспонованого торцевого добутку (або блокового стовпцевого добутку Хатрі-Рао) двох матриць $\mathbf {A} [\ast ]\mathbf {B}$ з однаковою кількістю стовпців у відповідних блоках справедливо[7]:

\mathbf {A} [\ast ]\mathbf {B} =\left[{\begin{array}{c | c}\mathbf {A} _{11}\ast \mathbf {B} _{11}&\mathbf {A} _{12}\ast \mathbf {B} _{12}\\\hline \mathbf {A} _{21}\ast \mathbf {B} _{21}&\mathbf {A} _{22}\ast \mathbf {B} _{22}\end{array}}\right]

.

Основні властивості

Транспонування:
$\left(\mathbf {A} [\ast ]\mathbf {B} \right)^{\textsf {T}}={\textbf {A}}^{\textsf {T}}[\bullet ]\mathbf {B} ^{\textsf {T}}$ [15]

Застосування

Родина торцевих добутків матриць стала основою започаткованої Слюсарем В. І. тензорно-матричної теорії цифрових антенних решіток для радіотехнічних систем[12], яка надалі отримала розвиток як частина теорії цифрової обробки сигналів.

Торцевий добуток набув широкого поширення в системах машинного навчання, статистичній обробці великих даних[17]. Він дозволяє скоротити обсяги обчислень при реалізації методу зменшення розмірності даних, що одержав назву тензорний скетч[17] а також швидкого перетворення Джонсона — Лінденштрауса[17]. При цьому здійснюється перехід від матриці великої розмірності до добутку Адамара, що оперує матрицями меншого розміру. Похибки апроксимації данних великої розмірності на основі торцевого добутку матриць задовольняють лемі Джонсона — Лінденштрауса[17][21]. У тому ж контексті ідея торцевого добутку може бути використана для вирішення завдання диференційної приватності (англ. differential privacy)[16]. Крім того, аналогічні обчислення були застосовані для формування тензорів співпадань в задачах обробки природної мови і побудови гіперграфів подібності зображень[22].

Торцевий добуток використаний у 2003 р. для P-сплайн апроксимації[19], у 2006 р. — для побудови узагальнених лінійних моделей масивів даних (GLAM) при їх статистичній обробці[20], а також для ефективної реалізації ядрових методів машинного навчання та дослідження взаємодії генотипів з оточуючим середовищем[23].

Див. також

Примітки

Khatri C. G., C. R. Rao (1968). Solutions to some functional equations and their applications to characterization of probability distributions. Sankhya 30: 167–180. Архів оригіналу за 23 жовтня 2010. Процитовано 21 серпня 2008.
Zhang X; Yang Z; Cao C. (2002). Inequalities involving Khatri–Rao products of positive semi-definite matrices. Applied Mathematics E-notes 2: 117–124.
See e.g. H.D. Macedo and J.N. Oliveira. A linear algebra approach to OLAP. Formal Aspects of Computing, 27(2):283–307, 2015.
Lev-Ari, Hanoch (1 січня 2005). Efficient Solution of Linear Matrix Equations with Application to Multistatic Antenna Array Processing. Communications in Information & Systems (EN) 05 (1): 123–130. ISSN 1526-7555. doi:10.4310/CIS.2005.v5.n1.a5.
Masiero, B.; Nascimento, V. H. (1 травня 2017). Revisiting the Kronecker Array Transform. IEEE Signal Processing Letters 24 (5): 525–529. Bibcode:2017ISPL...24..525M. ISSN 1070-9908. doi:10.1109/LSP.2017.2674969.
Vanderveen, M. C., Ng, B. C., Papadias, C. B., & Paulraj, A. (n.d.). Joint angle and delay estimation (JADE) for signals in multipath environments. Conference Record of The Thirtieth Asilomar Conference on Signals, Systems and Computers. — DOI:10.1109/acssc.1996.599145
Slyusar, V. I. (27 грудня 1996). End products in matrices in radar applications.. Radioelectronics and Communications Systems.– 1998, Vol. 41; Number 3: 50–53.
Anna Esteve, Eva Boj & Josep Fortiana (2009): Interaction Terms in Distance-Based Regression, Communications in Statistics — Theory and Methods, 38:19, P. 3501
Slyusar, V. I. (20 травня 1997). Analytical model of the digital antenna array on a basis of face-splitting matrix products.. Proc. ICATT- 97, Kyiv: 108–109.
Slyusar, V. I. (1999). A Family of Face Products of Matrices and its Properties. Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz 35 (3): 379–384. doi:10.1007/BF02733426.
Slyusar, V. I. (2003). Generalized face-products of matrices in models of digital antenna arrays with nonidentical channels. Radioelectronics and Communications Systems 46 (10): 9–17.
Миночкин А.И., Рудаков В.И., Слюсар В.И. (2012). Основы военно-технических исследований. Теория и приложения. Том. 2. Синтез средств информационного обеспечения вооружения и военной техники//Под ред. А.П. Ковтуненко. - Киев: «Гранмна». – 2012. с. C. 7 – 98; 354 – 521.
Slyusar, V. I. (15 вересня 1997). New operations of matrices product for applications of radars. Proc. Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED-97), Lviv.: 73–74.
C. Radhakrishna Rao. Estimation of Heteroscedastic Variances in Linear Models.//Journal of the American Statistical Association, Vol. 65, No. 329 (Mar., 1970), pp. 161—172
Vadym Slyusar. New Matrix Operations for DSP (Lecture). April 1999. - DOI: 10.13140/RG.2.2.31620.76164/1
Kasiviswanathan, Shiva Prasad, et al. «The price of privately releasing contingency tables and the spectra of random matrices with correlated rows.» Proceedings of the forty-second ACM symposium on Theory of computing. 2010.
Thomas D. Ahle, Jakob Bæk Tejs Knudsen. Almost Optimal Tensor Sketch. Published 2019. Mathematics, Computer Science, ArXiv
Ninh, Pham; Rasmus, Pagh (2013). Fast and scalable polynomial kernels via explicit feature maps SIGKDD international conference on Knowledge discovery and data mining. Association for Computing Machinery. doi:10.1145/2487575.2487591.
Eilers, Paul H.C.; Marx, Brian D. (2003). Multivariate calibration with temperature interaction using two-dimensional penalized signal regression.. Chemometrics and Intelligent Laboratory Systems 66 (2): 159–174. doi:10.1016/S0169-7439(03)00029-7.
Currie, I. D.; Durban, M.; Eilers, P. H. C. (2006). Generalized linear array models with applications to multidimensional smoothing. Journal of the Royal Statistical Society 68 (2): 259–280. doi:10.1111/j.1467-9868.2006.00543.x.
Ahle, Thomas; Kapralov, Michael; Knudsen, Jakob; Pagh, Rasmus; Velingker, Ameya; Woodruff, David; Zandieh, Amir (2020). Oblivious Sketching of High-Degree Polynomial Kernels ACM-SIAM Symposium on Discrete Algorithms. Association for Computing Machinery. doi:10.1137/1.9781611975994.9.
Bryan Bischof. Higher order co-occurrence tensors for hypergraphs via face-splitting. Published 15 February, 2020, Mathematics, Computer Science, ArXiv
Johannes W. R. Martini, Jose Crossa, Fernando H. Toledo, Jaime Cuevas. On Hadamard and Kronecker products in covariance structures for genotype x environment interaction.//Plant Genome. 2020;13:e20033. Page 5.

Джерела

Khatri C. G., C. R. Rao (1968). Solutions to some functional equations and their applications to characterization of probability distributions. Sankhya 30: 167–180. Архів оригіналу за 23 жовтня 2010. Процитовано 21 серпня 2008.
Zhang X; Yang Z; Cao C. (2002). Inequalities involving Khatri–Rao products of positive semi-definite matrices. Applied Mathematics E-notes 2: 117–124.
Matrix Algebra & Its Applications to Statistics & Econometrics./C. R. Rao with M. Bhaskara Rao. — World Scientific. — 1998. — P. 216.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Khatri C. G., C. R. Rao (1968). Solutions to some functional equations and their applications to characterization of probability distributions. Sankhya 30: 167–180. Архів оригіналу за 23 жовтня 2010. Процитовано 21 серпня 2008.

[2] Zhang X; Yang Z; Cao C. (2002). Inequalities involving Khatri–Rao products of positive semi-definite matrices. Applied Mathematics E-notes 2: 117–124.

[3] See e.g. H.D. Macedo and J.N. Oliveira. A linear algebra approach to OLAP. Formal Aspects of Computing, 27(2):283–307, 2015.

[4] Lev-Ari, Hanoch (1 січня 2005). Efficient Solution of Linear Matrix Equations with Application to Multistatic Antenna Array Processing. Communications in Information & Systems (EN) 05 (1): 123–130. ISSN 1526-7555. doi:10.4310/CIS.2005.v5.n1.a5.

[5] Masiero, B.; Nascimento, V. H. (1 травня 2017). Revisiting the Kronecker Array Transform. IEEE Signal Processing Letters 24 (5): 525–529. Bibcode:2017ISPL...24..525M. ISSN 1070-9908. doi:10.1109/LSP.2017.2674969.

[6] Vanderveen, M. C., Ng, B. C., Papadias, C. B., & Paulraj, A. (n.d.). Joint angle and delay estimation (JADE) for signals in multipath environments. Conference Record of The Thirtieth Asilomar Conference on Signals, Systems and Computers. — DOI:10.1109/acssc.1996.599145

[slyusar-7] Slyusar, V. I. (27 грудня 1996). End products in matrices in radar applications.. Radioelectronics and Communications Systems.– 1998, Vol. 41; Number 3: 50–53.

[Fortiana-8] Anna Esteve, Eva Boj & Josep Fortiana (2009): Interaction Terms in Distance-Based Regression, Communications in Statistics — Theory and Methods, 38:19, P. 3501

[slyusar1-9] Slyusar, V. I. (20 травня 1997). Analytical model of the digital antenna array on a basis of face-splitting matrix products.. Proc. ICATT- 97, Kyiv: 108–109.

[slyusar2-10] Slyusar, V. I. (1999). A Family of Face Products of Matrices and its Properties. Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz 35 (3): 379–384. doi:10.1007/BF02733426.

[11] Slyusar, V. I. (2003). Generalized face-products of matrices in models of digital antenna arrays with nonidentical channels. Radioelectronics and Communications Systems 46 (10): 9–17.

[slyusarsmartantenna1-12] Миночкин А.И., Рудаков В.И., Слюсар В.И. (2012). Основы военно-технических исследований. Теория и приложения. Том. 2. Синтез средств информационного обеспечения вооружения и военной техники//Под ред. А.П. Ковтуненко. - Киев: «Гранмна». – 2012. с. C. 7 – 98; 354 – 521.

[DIPED-13] Slyusar, V. I. (15 вересня 1997). New operations of matrices product for applications of radars. Proc. Direct and Inverse Problems of Electromagnetic and Acoustic Wave Theory (DIPED-97), Lviv.: 73–74.

[Rao-14] C. Radhakrishna Rao. Estimation of Heteroscedastic Variances in Linear Models.//Journal of the American Statistical Association, Vol. 65, No. 329 (Mar., 1970), pp. 161—172

[lecture-15] Vadym Slyusar. New Matrix Operations for DSP (Lecture). April 1999. - DOI: 10.13140/RG.2.2.31620.76164/1

[k2010-16] Kasiviswanathan, Shiva Prasad, et al. «The price of privately releasing contingency tables and the spectra of random matrices with correlated rows.» Proceedings of the forty-second ACM symposium on Theory of computing. 2010.

[tensorsketch-17] Thomas D. Ahle, Jakob Bæk Tejs Knudsen. Almost Optimal Tensor Sketch. Published 2019. Mathematics, Computer Science, ArXiv

[ninh-18] Ninh, Pham; Rasmus, Pagh (2013). Fast and scalable polynomial kernels via explicit feature maps SIGKDD international conference on Knowledge discovery and data mining. Association for Computing Machinery. doi:10.1145/2487575.2487591.

[spline-19] Eilers, Paul H.C.; Marx, Brian D. (2003). Multivariate calibration with temperature interaction using two-dimensional penalized signal regression.. Chemometrics and Intelligent Laboratory Systems 66 (2): 159–174. doi:10.1016/S0169-7439(03)00029-7.

[GLAM-20] Currie, I. D.; Durban, M.; Eilers, P. H. C. (2006). Generalized linear array models with applications to multidimensional smoothing. Journal of the Royal Statistical Society 68 (2): 259–280. doi:10.1111/j.1467-9868.2006.00543.x.

[highdeg-21] Ahle, Thomas; Kapralov, Michael; Knudsen, Jakob; Pagh, Rasmus; Velingker, Ameya; Woodruff, David; Zandieh, Amir (2020). Oblivious Sketching of High-Degree Polynomial Kernels ACM-SIAM Symposium on Discrete Algorithms. Association for Computing Machinery. doi:10.1137/1.9781611975994.9.

[22] Bryan Bischof. Higher order co-occurrence tensors for hypergraphs via face-splitting. Published 15 February, 2020, Mathematics, Computer Science, ArXiv

[23] Johannes W. R. Martini, Jose Crossa, Fernando H. Toledo, Jaime Cuevas. On Hadamard and Kronecker products in covariance structures for genotype x environment interaction.//Plant Genome. 2020;13:e20033. Page 5.