Ядрові методи

Ядрові методи можливо розглядати як навчання на прикладах: замість навчання якогось фіксованого набору параметрів, які відповідають ознакам їхніх входів, вони натомість «запам'ятовують» ${\displaystyle i}$-тий тренувальний зразок ${\displaystyle (\mathbf {x} _{i},y_{i})}$ та навчаються відповідної йому ваги ${\displaystyle w_{i}}$. Для даних, відсутніх у тренувальному наборі, передбачення здійснюється застосуванням функції подібності ${\displaystyle k}$, яку називають ядром (англ. kernel), до неміченого входу ${\displaystyle \mathbf {x'} }$ та кожного із тренувальних входів ${\displaystyle \mathbf {x} _{i}}$. Наприклад, ядрований бінарний класифікатор зазвичай обчислює зважену суму подібностей

${\displaystyle {\hat {y}}=\operatorname {sgn} \sum _{i=1}^{n}w_{i}y_{i}k(\mathbf {x} _{i},\mathbf {x'} )}$,

де

• ${\displaystyle {\hat {y}}\in \{-1,+1\}}$ є передбаченою ядрованим бінарним класифікатором міткою для неміченого входу ${\displaystyle \mathbf {x'} }$, справжня прихована мітка ${\displaystyle y}$ якого нас і цікавить;
• ${\displaystyle k\colon {\mathcal {X}}\times {\mathcal {X}}\to \mathbb {R} }$ є ядровою функцією, яка вимірює подібність будь-якої пари входів ${\displaystyle \mathbf {x} ,\mathbf {x'} \in {\mathcal {X}}}$;
• сума пробігає n мічених зразків ${\displaystyle \{(\mathbf {x} _{i},y_{i})\}_{i=1}^{n}}$ тренувального набору класифікатора, де ${\displaystyle y_{i}\in \{-1,+1\}}$;
• ${\displaystyle w_{i}\in \mathbb {R} }$ є вагами тренувальних зразків, визначеними згідно алгоритму навчання;
• функція знаку ${\displaystyle \operatorname {sgn} }$ визначає, чи виходить передбачена класифікація ${\displaystyle {\hat {y}}}$ позитивною, чи негативною.

Ядрові класифікатори було описано ще в 1960-х роках із винайденням ядрового перцептрону.[2] Вони досягли великого піднесення разом з популярністю опорно-векторних машин (ОВМ) у 1990-х роках, коли було виявлено, що ОВМ є конкурентноздатними в порівнянні зі нейронними мережами на таких задачах як розпізнавання рукописного введення.

ОВМ з ядром, заданим φ((a, b)) = (a, b, a² + b²), і відтак K(x, y) = x•y + x² y². Тренувальні точки відображено до 3-вимірного простору, де легко знайти розділову гіперплощину.

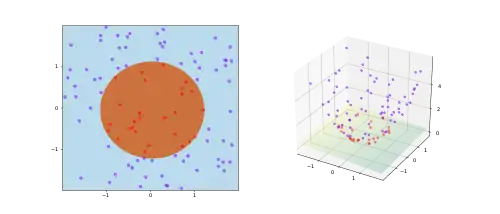
Ядровий трюк уникає явного відображення, потрібного для тощо, щоби лінійні алгоритми навчання навчалися нелінійної функції або межі рішень. Для всіх ${\displaystyle \mathbf {x} }$ та ${\displaystyle \mathbf {x'} }$ у вхідному просторі ${\displaystyle {\mathcal {X}}}$ певні функції ${\displaystyle k(\mathbf {x} ,\mathbf {x'} )}$ може бути виражено як внутрішній добуток в іншому просторі ${\displaystyle {\mathcal {V}}}$. Функцію ${\displaystyle k\colon {\mathcal {X}}\times {\mathcal {X}}\to \mathbb {R} }$ часто називають ядром або ядровою функцією. Слово «ядро» використовують в математиці для позначення зважувальної функції зваженої суми або інтегралу.

Деякі задачі в машинному навчанні мають складнішу структуру, ніж просто довільна зважувальна функція ${\displaystyle k}$. Обчислювання робиться набагато простішим, якщо ядро може бути записано в вигляді «відображення ознак» ${\displaystyle \varphi \colon {\mathcal {X}}\to {\mathcal {V}}}$, яке задовольняє

${\displaystyle k(\mathbf {x} ,\mathbf {x'} )=\langle \varphi (\mathbf {x} ),\varphi (\mathbf {x'} )\rangle _{\mathcal {V}}.}$

Ключовим обмеженням є те, що ${\displaystyle \langle \cdot ,\cdot \rangle _{\mathcal {V}}}$ мусить бути власним внутрішнім добутком. З іншого боку, явне представлення ${\displaystyle \varphi }$ не є необхідним, поки ${\displaystyle {\mathcal {V}}}$ є простором з внутрішнім добутком. Ця альтернатива випливає з теореми Мерсера: неявно визначена функція ${\displaystyle \varphi }$ існує тоді, коли простір ${\displaystyle {\mathcal {X}}}$ може бути споряджено придатною мірою, яка забезпечувала би, щоби функція ${\displaystyle k}$ задовольняла умову Мерсера.

Теорема Мерсера є подібною до узагальнення того наслідку з лінійної алгебри, що пов'язує внутрішній добуток із будь-якою додатноозначеною матрицею. Фактично, умову Мерсера може бути зведено до цього простішого прояву. Якщо ми оберемо як нашу міру лічильну міру ${\displaystyle \mu (T)=|T|}$ для всіх ${\displaystyle T\subset X}$, яка лічить число точок всередині множини ${\displaystyle T}$, то інтеграл у теоремі Мерсера зводиться до підсумовування

${\displaystyle \sum _{i=1}^{n}\sum _{j=1}^{n}k(\mathbf {x} _{i},\mathbf {x} _{j})c_{i}c_{j}\geqslant 0.}$

Якщо це підсумовування виконується для всіх скінченних послідовностей точок ${\displaystyle (\mathbf {x} _{1},\dotsc ,\mathbf {x} _{n})}$ в ${\displaystyle {\mathcal {X}}}$ і всіх варіантів вибору ${\displaystyle n}$ дійснозначних коефіцієнтів ${\displaystyle (c_{1},\dots ,c_{n})}$ (пор. додатноозначене ядро), то функція ${\displaystyle k}$ задовольняє умову Мерсера.

Деякі алгоритми, які залежать від довільних взаємозв'язків у рідному просторі ${\displaystyle {\mathcal {X}}}$, фактично мають лінійну інтерпретацію за іншої постановки: області значень ${\displaystyle \varphi }$. Лінійна інтерпретація дає нам прояснення алгоритму. Понад те, часто немає потреби під час обчислень обчислювати ${\displaystyle \varphi }$ безпосередньо, як у випадку методу опорних векторів. Деякі дослідники посилаються на цю раціоналізацію часу як на головну перевагу. Дослідники також використовують її для обґрунтування сенсу та властивостей наявних алгоритмів.

Теоретично, матриця Грама ${\displaystyle \mathbf {K} \in \mathbb {R} ^{n\times n}}$ по відношенню до ${\displaystyle \{\mathbf {x} _{1},\dotsc ,\mathbf {x} _{n}\}}$ (яку іноді також називають «ядровою матрицею», англ. "kernel matrix"[3]), мусить бути додатно напівозначеною.[4] Емпірично, для евристик машинного навчання варіанти обрання функції ${\displaystyle k}$, які не задовольняють умову Мерсера, все ще можуть працювати прийнятно, якщо ${\displaystyle k}$ щонайменше наближує інтуїтивне уявлення про подібність.[5] Незалежно від того, чи є ${\displaystyle k}$ мерсеровим ядром, ${\displaystyle k}$ все одно можуть називати «ядром».

Якщо ядрова функція ${\displaystyle k}$ є також і функцією коваріації, як при застосуванні в ґаусових процесах, то матриця Грама ${\displaystyle \mathbf {K} }$ можуть також називати коваріаційною матрицею.[6]

Сфери застосування ядрових методів є різноманітними, до них належать геостатистика,[7] кригінг, зважування зворотних відстаней, об'ємна відбудова, біоінформатика, хемоінформатика, витягування інформації та розпізнавання рукописного введення.

• Ядро Фішера
• Графові ядра
• Ядрове згладжування
• Поліноміальне ядро
• РБФ-ядро
• Стрічкові ядра

• Ядрові методи для отримування векторних результатів
• Теорема про представлення

• Kernel-Machines Org — вебсайт спільноти (англ.)
• www.support-vector-machines.org (література, огляд, програмне забезпечення, посилання пов'язані з методом опорних векторів — академічний сайт) (англ.)
• Стаття Kernel Methods на onlineprediction.net (англ.)