Відліковий скетч
Відліковий скетч (англ. Count sketch) — метод зменшення розмірності, що використовується у статистиці, машинному навчанні та алгоритмах обробки великих даних[1][2]. Він може бути використаний для прискорення ядрових методів та білінійного пулінга у нейронних мережах, а також застосовується у багатьох числових алгоритмах лінійної алгебри[3].
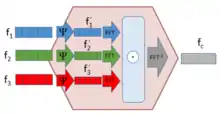
Особливості
На відміну від тензорного скетчу відліковий скетч оперує так званим зовнішнім добутком векторів:
- ,
де означає добуток Кронекера.
Суттєво, що відліковий скетч від зовнішнього добутку двох векторів
еквівалентний векторній згортці
- ,
де і є незалежними матрицями.
Для прискореного обчислення згортки відлікових скетчів може бути задіяне швидке перетворення Фур'є. У цьому випадку завдяки використанню торцевого добутку матриць[5][6][7] для факторизації матриці скетчу відповідні структури можуть бути розраховані значно швидше.
Див. також
Примітки
- Faisal M. Algashaam; Kien Nguyen; Mohamed Alkanhal; Vinod Chandran; Wageeh Boles.Multispectral Periocular Classification WithMultimodal Compact Multi-Linear Pooling [1]. — IEEE Access, Vol. 5. 2017.
- Ahle, Thomas; Knudsen, Jakob (3 вересня 2019). Almost Optimal Tensor Sketch. Researchgate. Процитовано 11 липня 2020.
- Woodruff, David P. «Sketching as a Tool for Numerical Linear Algebra.» Theoretical Computer Science 10.1-2 (2014): 1–157.
- Ninh, Pham; Rasmus, Pagh (2013). Fast and scalable polynomial kernels via explicit feature maps SIGKDD international conference on Knowledge discovery and data mining. Association for Computing Machinery. doi:10.1145/2487575.2487591.
- Slyusar, V. I. (27 грудня 1996). End products in matrices in radar applications.. Radioelectronics and Communications Systems.– 1998, Vol. 41; Number 3: 50–53.
- Slyusar, V. I. (20 травня 1997). Analytical model of the digital antenna array on a basis of face-splitting matrix products.. Proc. ICATT-97, Kyiv: 108–109.
- Slyusar, V. I. (13 березня 1998). A Family of Face Products of Matrices and its Properties. Cybernetics and Systems Analysis C/C of Kibernetika I Sistemnyi Analiz.- 1999. 35 (3): 379–384. doi:10.1007/BF02733426.
