Еліпс Штейнера
Існує єдине афінне перетворення, яке переводить правильний трикутник у даний трикутник. Образ вписаного кола правильного трикутника при такому перетворенні є еліпсом, який називають вписаним еліпсом Штейнера, а образ описаного кола також є еліпсом, який називають описаним еліпсом Штейнера.[1]

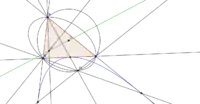
Вписаний і описаний еліпси Штейнера для трикутника. Показані червоним кольором
Визначення вписаного еліпса Штейнера
- У трикутник можна вписати нескінченно багато еліпсів.
- Однак у трикутник можна вписати єдиний еліпс, який дотикається до сторін в їх серединах. Такий еліпс називається вписаним еліпсом Штейнера. Його перспектором буде центроїд трикутника.
- Визначення перспектора коніки (включно з конікою-еліпсом) див. нижче.
Визначення описаного еліпса Штейнера
- Навколо трикутника можна описати нескінченно багато еліпсів.
- Однак навколо трикутника можна описати єдиний еліпс, який дотикається до прямих, що проходять через вершини і паралельні сторонам. Такий еліпс називають описаним еліпсом Штейнера.
- Фокуси описаного еліпса Штейнера називають точками Скутіна.
- Чевіани, проведені через фокуси описаного еліпса Штейнера (точки Скутіна), рівні (теорема Скутина).
Афінне перетворення еліпса Штейнера
Якщо афінним перетворенням («перекосом») перевести довільний різнобічний трикутник у правильний трикутник, то його вписаний і описаний еліпси Штейнера перейдуть у вписане й описане кола.
Визначення перспектив коніки
- У трикутник можна вписати нескінченно багато конік (еліпсів, парабол або гіпербол).
- Якщо в трикутник вписати довільну конку і з'єднати точки дотику з протилежними вершинами, то отримані прямі перетнуться в одній точці, званій перспектором коніки.
- Для будь-якої точки площини, що не лежить на стороні або на її продовженні існує вписана коніка з перспектором у цій точці.
Властивості
- Вписаний еліпс Штейнера має найбільшу площу серед усіх еліпсів, вписаних у даний трикутник, а описаний — найменшу серед усіх описаних.
- Вписаний еліпс Штейнера - еліпс, вписаний у трикутник, який дотикається до середин його сторін.

Властивості вписаної параболи
Парабола Кіперта
- (Теорема Мардена) фокуси вписаного еліпса Штейнера є екстремальними точками многочлена третього степеня з коренями у вершинах трикутника на комплексній площині.
- Перспектори вписаних у трикутник парабол лежать на описаному еліпсі Штейнера. Фокус вписаної параболи лежить на описаному колі, а директриса проходить через ортоцентр. Параболу, вписану в трикутник, що має директрисою пряму Ейлера, називають параболою Кіперта. Її перспектор — четверта точка перетину описаного кола і описаного еліпса Штейнера, називана точкою Штейнера.
Примітки
- Weisstein, E. «Steiner Inellipse» — From MathWorld, A Wolfram Web Resource, http://mathworld.wolfram.com/SteinerInellipse.html.
Див. також
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
