Еліптичні функції Якобі

Еліптичні функції Якобі — набір основних еліптичних функцій комплексної змінної, і допоміжних тета-функцій, які мають велике історичне значення і пряме відношення до деяких прикладних задач (наприклад, рівняння маятника). Вони також мають корисні аналогії з тригонометричними функціями, як показує відповідне позначення $\operatorname {\mathrm {sn} }$ для $\sin$ . Вони не дають найпростіший спосіб розвинути загальну теорію еліптичних функцій, тому в у вступних книгах вони менш популярні, ніж еліптичні функції Вейєрштраса. Еліптичні функції Якобі мають в основному паралелограмі по два простих полюси і два простих нуля.

Означення

Як мероморфні функції

Паралелограм Якобі.

Функції Якобі є еліптичними функціями, тобто подвійно періодичними мероморфними функціями комплексної змінної. Тобто фактично їх значення визначається на торі або основному паралелограмі.

Якщо ця функція є всюди голоморфною то згідно з теоремою Ліувіля вона буде константою. З властивостей лишків та подвійної періодичності випливає також, що еліптичні функції не можуть в основному паралелограмі мати єдиного полюса порядку 1. Відповідно найпростішими несталими функціями є функції з єдиним полюсом порядку два і двома полюсами порядку 1. Першими є еліптичні функції Вейєрштраса, другими — еліптичні функції Якобі.

Загалом існує 12 принципово відмінних еліптичних функцій Якобі. Загалом вони залежать від основного паралелограма.

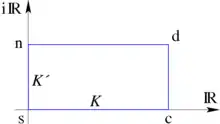
Нехай визначено паралелограм (який не буде основним) як на малюнку з вершинами 0, K, K + iK′, iK′, що для зручності нотації позначені як s, c, d і n, відповідно.

Дійсні числа K і K' називаються «чвертями періодів».

12 функцій позначаються sc, sd, sn, cd, cn, cs, dn, ds, dc, ns, nc і nd.

Вони є єдиними еліптичними функціями, що задовольняють умови:

Функція має простий нуль в куті p визначеного паралелограма і простий полюс в куті q. В інших двох кутах полюсів і нулів немає.
Відстань від p до q є половиною періоду функції pq u;тобто функція pq u є періодичною в напрямку pq, з періодом вдвічі більшим, ніж відстань від p до q. Відстані від p до інших точок є чвертями періодів.
Розклад функції pq u в ряд Тейлора щодо u в околі точки p має членом найменшого степеня u; членом найменшого степеня при розкладі в ряд Лорана в околі q є 1/u; в інших кутах розклад в ряд Тейлора починається з 1.

Наприклад функція dn має нуль в точці d і полюс в точці n. Вона періодична з періодами 2K і 4iK.

Як обернені функції до еліптичних інтегралів

Наведене вище означення в термінах мероморфних функцій є досить абстрактним. Існує більш просте, але абсолютно еквівалентне означення, що задає еліптичні функції як зворотні до неповного еліптичному інтегралу першого роду. нехай

u=\int \limits _{0}^{\phi }{\frac {d\theta }{\sqrt {1-m\sin ^{2}\theta }}}.

Еліптична функція $sn~u$ задається як

\operatorname {sn} \;u=\sin \phi

і $cn~u$ визначається

\operatorname {cn} \;u=\cos \phi

а

\operatorname {dn} \;u={\sqrt {1-m\sin ^{2}\phi }}.

Тут кут $\phi$ називається амплітудою. $\operatorname {dn} \;u=\Delta (u)$ називається дельта амплітудою. Значення m є вільним параметром, який є дійсним числом в діапазоні $0\leq m\leq 1$ , і таким чином еліптичні функції є функціями двох аргументів: амплітуди $\phi$ і параметра m.

Решта дев'ять еліптичних функцій легко побудувати з трьох вищенаведених. Це буде зроблено нижче.

Коли $\phi =\pi /2$ , то u дорівнює чверті періоду K.

Означення в термінах тета-функцій

Еквівалентно еліптичні функції Якобі можна визначити в термінах тета-функцій. Якщо ми визначимо $\vartheta (0;\tau )$ як $\vartheta$ , і $\vartheta _{01}(0;\tau ),\vartheta _{10}(0;\tau ),\vartheta _{11}(0;\tau )$ відповідно як $\vartheta _{01},\vartheta _{10},\vartheta _{11}$ (тета константи) тоді еліптичний модуль k дорівнює $k=\left({\vartheta _{10} \over \vartheta }\right)^{2}$ . Вважаючи $u=\pi \vartheta ^{2}z$ , отримаємо

{\begin{aligned}\operatorname {sn} (u;k)&=-{\vartheta \vartheta _{11}(z;\tau ) \over \vartheta _{10}\vartheta _{01}(z;\tau )}\\[7pt]\operatorname {cn} (u;k)&={\vartheta _{01}\vartheta _{10}(z;\tau ) \over \vartheta _{10}\vartheta _{01}(z;\tau )}\\[7pt]\operatorname {dn} (u;k)&={\vartheta _{01}\vartheta (z;\tau ) \over \vartheta \vartheta _{01}(z;\tau )}\end{aligned}}

Оскільки функції Якобі визначаються в термінах еліптичного модуля $k(\tau )$ , необхідно знайти обернені до них і записати τ в термінах k. Почнемо з додаткового модуля $k'={\sqrt {1-k^{2}}}$ . Як функція від τ він рівний

k'(\tau )=({\vartheta _{01} \over \vartheta })^{2}.

Введемо позначення

\ell ={1 \over 2}{1{\sqrt {k'}} \over 1+{\sqrt {k'}}}={1 \over 2}{\vartheta -\vartheta _{01} \over \vartheta +\vartheta _{01}}.

Визначимо також ном q як $q=\exp(\pi i\tau )$ і розкладемо $\ell$ в ряд за степенями нома q. отримаємо

\ell ={q+q^{9}+q^{25}+\cdots  \over 1+2q^{4}+2q^{16}+\cdots }.

Можна записати розклад в ряд

q=\ell +2\ell ^{5}+15\ell ^{9}+150\ell ^{13}+1707\ell ^{17}+20910\ell ^{21}+268616\ell ^{25}+\cdots .

Оскільки ми можемо розглянути окремий випадок коли уявна частина τ більша або рівна ${\sqrt {3}}/2$ , ми можемо сказати, що значення q менше або рівне $\exp(-\pi {\sqrt {3}}/2)$ . Для таких малих значень вищенаведений ряд збігається дуже швидко, і це дозволяє легко знайти відповідне значення для q.

Позначення

Для еліптичних функцій можна зустріти різноманітні позначення. Еліптичні функції — функції двох змінних. Першу змінну можна дати в термінах амплітуди φ, або зазвичай, в термінах u, як нижче. Другу змінну можна було б дати в термінах параметра m, або як еліптичний модуль k, де $k^{2}=m$ , або в термінах модулярного кута $o\!\varepsilon$ , де $m=\sin ^{2}o\varepsilon$ .

Інші функції

Зміною двох букв в назві функцій зазвичай позначають обернені функції до трьох основних функцій наведених вище:

{\begin{aligned}\operatorname {ns} (u)&={\frac {1}{\operatorname {sn} (u)}}\\[8pt]\operatorname {nc} (u)&={\frac {1}{\operatorname {cn} (u)}}\\[8pt]\operatorname {nd} (u)&={\frac {1}{\operatorname {dn} (u)}}\end{aligned}}

Частки трьох головних функцій позначають першою літерою чисельника і першою літерою знаменника:

{\begin{aligned}\operatorname {sc} (u)&={\frac {\operatorname {sn} (u)}{\operatorname {cn} (u)}}\\[8pt]\operatorname {sd} (u)&={\frac {\operatorname {sn} (u)}{\operatorname {dn} (u)}}\\[8pt]\operatorname {dc} (u)&={\frac {\operatorname {dn} (u)}{\operatorname {cn} (u)}}\\[8pt]\operatorname {ds} (u)&={\frac {\operatorname {dn} (u)}{\operatorname {sn} (u)}}\\[8pt]\operatorname {cs} (u)&={\frac {\operatorname {cn} (u)}{\operatorname {sn} (u)}}\\[8pt]\operatorname {cd} (u)&={\frac {\operatorname {cn} (u)}{\operatorname {dn} (u)}}\end{aligned}}

Для кращого запам'ятовування більш коротко можна записати : $\operatorname {pq} (u)={\frac {\operatorname {pr} (u)}{\operatorname {qr(u)} }}$ де всі букви p, q, і r є будь-якими буквами s, c, d, n (слід пам'ятати, що ss = cc = dd = nn = 1).

Додаткові теореми

Функції задовольняють двом алгебраїчним співвідношенням

\operatorname {cn} ^{2}(u,k)+\operatorname {sn} ^{2}(u,k)=1,\,

\operatorname {dn} ^{2}(u,k)+k^{2}\operatorname {sn} ^{2}(u,k)=1.\,

З цього видно, що (cn, sn, dn) параметризують еліптичну криву, яка є перетином двох квадрик заданих вищезазначеними двома рівняннями.

На цій кривій можна визначити груповий закон для точок за допомогою додаткових формул для функцій Якобі:

{\begin{aligned}\operatorname {cn} (x+y)&={\operatorname {cn} (x)\operatorname {cn} (y)-\operatorname {sn} (x)\operatorname {sn} (y)\operatorname {dn} (x)\operatorname {dn} (y) \over {1-k^{2}\operatorname {sn} ^{2}(x)\operatorname {sn} ^{2}(y)}},\\[8pt]\operatorname {sn} (x+y)&={\operatorname {sn} (x)\operatorname {cn} (y)\operatorname {dn} (y)+\operatorname {sn} (y)\operatorname {cn} (x)\operatorname {dn} (x) \over {1-k^{2}\operatorname {sn} ^{2}(x)\operatorname {sn} ^{2}(y)}},\\[8pt]\operatorname {dn} (x+y)&={\operatorname {dn} (x)\operatorname {dn} (y)-k^{2}\operatorname {sn} (x)\operatorname {sn} (y)\operatorname {cn} (x)\operatorname {cn} (y) \over {1-k^{2}\operatorname {sn} ^{2}(x)\operatorname {sn} ^{2}(y)}}.\end{aligned}}

Тригонометричні і гіперболічні функції, як окремий випадок еліптичних

Якщо m = 1, то: $u=\int \limits _{0}^{\varphi }{\frac {d\theta }{\sqrt {1\sin ^{2}{\theta }}}}=\operatorname {ln} \left({\frac {1}{\cos \varphi }}-\operatorname {tg} \varphi \right)$ ;

Звідси:

\sin \varphi =\operatorname {sn} \,u={\frac {e^{u}-1}{e^{u}+1}}=\operatorname {th} \,u

Звідси:

\operatorname {cn} \,u={\sqrt {1\operatorname {sn} ^{2}\,u}}={\frac {1}{\operatorname {ch} \,u}}

і:

\operatorname {dn} \,u={\sqrt {1\operatorname {sn} ^{2}\,u}}={\frac {1}{\operatorname {ch} \,u}}

Таким чином, при m = 1 еліптичні функції вироджуються в гіперболічні.

Якщо m = 0, то: $u=\int \limits _{0}^{\varphi }d\theta =\varphi$ ;

Звідси:

\sin \varphi =\sin \,u=\operatorname {sn} \,u

,

а також:

\operatorname {cn} \,u=\cos \,u

,:

\operatorname {dn} \,u=1

,

Таким чином, при m = 0 еліптичні функції вироджуються в тригонометричні.

Співвідношення між квадратами функцій

Для квадратів цих функцій вірні наступні співвідношення:

-\operatorname {dn} ^{2}(u)+m_{1}=-m\;\operatorname {cn} ^{2}(u)=m\;\operatorname {sn} ^{2}(u)-m

-m_{1}\;\operatorname {nd} ^{2}(u)+m_{1}=-mm_{1}\;\operatorname {sd} ^{2}(u)=m\;\operatorname {cd} ^{2}(u)-m

:

m_{1}\;\operatorname {sc} ^{2}(u)+m_{1}=m_{1}\;\operatorname {nc} ^{2}(u)=\operatorname {dc} ^{2}(u)-m

\operatorname {cs} ^{2}(u)+m_{1}=\operatorname {ds} ^{2}(u)=\operatorname {ns} ^{2}(u)-m

де

m+m_{1}=1

і

m=k^{2}

.

Додаткові рівності для квадратів можна отримати якщо зауважити, що $\operatorname {pq} ^{2}\cdot \operatorname {qp} ^{2}=1$ , а також $\operatorname {pq} =\operatorname {pr} /\operatorname {qr}$ де p, q, r — будь-які літери s, c, d, n і ss = cc = dd = nn = 1.

Ном

Нехай ном дорівнює $q=\exp(-\pi K'/K)$ і нехай аргумент — $v=\pi u/(2K)$ .

Тоді функції можна представити у вигляді сум Ламберта:

\operatorname {sn} (u)={\frac {2\pi }{K{\sqrt {m}}}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1-q^{2n+1}}}\sin((2n+1)v),

\operatorname {cn} (u)={\frac {2\pi }{K{\sqrt {m}}}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1+q^{2n+1}}}\cos((2n+1)v),

\operatorname {dn} (u)={\frac {\pi }{2K}}+{\frac {2\pi }{K}}\sum _{n=1}^{\infty }{\frac {q^{n}}{1+q^{2n}}}\cos(2nv).

Розв'язки нелінійних звичайних диференціальних рівнянь

Похідні трьох основних еліптичних функцій Якобі записуються у вигляді:

{\frac {\mathrm {d} }{\mathrm {d} z}}\,\mathrm {sn} \,(z;k)=\mathrm {cn} \,(z;k)\,\mathrm {dn} \,(z;k),

{\frac {\mathrm {d} }{\mathrm {d} z}}\,\mathrm {cn} \,(z;k)=-\mathrm {sn} \,(z;k)\,\mathrm {dn} \,(z;k),

{\frac {\mathrm {d} }{\mathrm {d} z}}\,\mathrm {dn} \,(z;k)=-k^{2}\mathrm {sn} \,(z;k)\,\mathrm {cn} \,(z;k).

Використовуючи теорему, формулювання якої наведена вище отримаємо для заданого k (0 < k < 1) рівняння розв'язками яких є еліптичні функції Якобі:

$\mathrm {sn} \,(x;k)$ є розв'язком рівнянь

{\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1+k^{2})y-2k^{2}y^{3}=0,

і

\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-k^{2}y^{2})

$\mathrm {cn} \,(x;k)$ є розв'язком рівнянь

{\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1-2k^{2})y+2k^{2}y^{3}=0,

і

\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-k^{2}+k^{2}y^{2})

$\mathrm {dn} \,(x;k)$ є розв'язком рівняння

{\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}-(2-k^{2})y+2y^{3}=0,

і

\left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(y^{2}-1)(1-k^{2}-y^{2})

Див. також

Посилання

Hazewinkel, Michiel, ред. (2001). Jacobi elliptic functions. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
Weisstein, Eric W. Jacobi Elliptic Functions(англ.) на сайті Wolfram MathWorld.

Література

Abramowitz, Milton; Stegun, Irene A. eds. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover. ISBN 0-486-61272-4. See Chapter 16

Н. И. Ахиезер (1970). Элементы теории эллиптических функций. Москва: Наука.

Дж. Н. Ватсон, Э. Т. Уиттекер (1963). Курс современного анализа. Ч.2. Трансцендентные функции. Москва: Мир. или Москва: УРСС, 2010

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.