Коваріаційна матриця
Коваріаційна матриця (або коваріаційна таблиця) в теорії ймовірностей — це квадратна матриця, яка складена з попарних коваріацій і дисперсій двох або більше випадкових величин.
| Частина з циклу Статистика |
| Кореляція та коваріація |
|---|
|
Для випадкових векторів
|
|
Для стохастичних процесів |
|
Для детермінованих сигналів
|

Двовимірна ґаусова функція густини ймовірності з центром в (0, 0) та коваріаційною матрицею [ 1.00, 0.50 ; 0.50, 1.00 ].
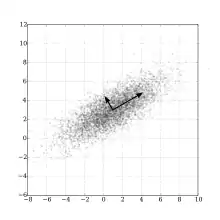
Точки вибірки з багатовимірного нормального розподілу зі стандартним відхиленням 3 у приблизно ліво-верхньому прямому напрямку та 1 у перпендикулярному напрямку. Оскільки складові x та y мають коваріацію, дисперсії x та y описують цей розподіл не повністю. Необхідна коваріаційна матриця 2×2; напрямки стрілок відповідають власним векторам цієї матриці коваріації, а їхні довжини — квадратним кореням власних значень.
Визначення
- нехай , — два випадкових вектора розмірності і відповідно. Нехай також випадкові величини мають скінченний другий момент, тобто . Тоді матрицею коваріації називається
тобто
- ,
де
- .
- Якщо , то називається матрицею коваріації вектора і позначається . Така матриця коваріацій є узагальненням дисперсії для багатовимірної випадкової величини, а її слід — скалярним виразом дисперсії багатовимірної випадкової величини. Власні вектори і власні значення цієї матриці дозволяють оцінити розміри і форму хмари розподілу випадкової величини, апроксимувавши її еліпсоїдом (або еліпсом у двовимірному випадку) .
Зауваження
- Цей термін має також інші значення. Наприклад, матрицею коваріації називається матриця, складена з попарних коваріацій різних елементів одного випадкового вектора.
Властивості
- Скорочена формула для обчислення матриці коваріації:
- .
- Матриця коваріації випадкового вектора невід'ємно визначена:
- .
- Зміна масштабу:
- .
- Якщо випадкові вектори і некорельовані (), то
- .
- Матриця коваріації афінного перетворення:
- ,
де — довільна матриця розмірності , а .
- Перестановка аргументів:
- Матриця коваріації адитивна за кожним аргументом:
- ,
- .
- Якщо і незалежні, то
- .
Особливість
- Згідно з законом додавання дисперсій, алгебраїчна сума значень коваріаційної матриці системи випадкових величин дорівнює дисперсії суми цих величин.
Теорема
- Якщо величини утворюють коло K, коло L або коло M, тоді алгебраїчна сума значень будь-якого стовпчика або рядка коваріаційної матриці системи таких величин дорівнює нулю[1].
Джерела інформації
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.