Багатовимірний нормальний розподіл
Багатовимірний нормальний розподіл (чи багатовимірний гаусів розподіл) у теорії ймовірностей — це узагальнення одновимірного нормального розподілу для випадку із багатьма вимірами. Відповідно до одного із визначень стверджують, що вектор випадкових величин має k-варіативний нормальний розподіл якщо кожна лінійна комбінація його k компонент має одновимірний нормальний розподіл. В основному його важливість випливає із узагальнення центральної граничної теореми для багатьох вимірів. Багатовимірний нормальний розподіл часто використовують аби описати, принаймні наближено, будь-яку множину (можливо) корельованих випадкових величин із дійсними значенням, кожна з яких скупчується довкола середнього значення.
| Багатовимірний нормальний розподіл | |
|---|---|
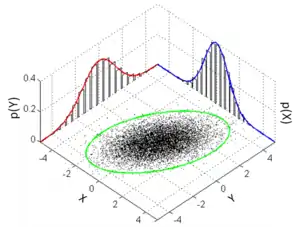 Множина точок, що представляють елементарні події багатовимірного нормального розподілу із і , разом з якими показано еліпс розміром в 3-сігми, два маргінальні розподіли і дві 1-вимірні гістограми. | |
| Параметри |
μ ∈ Rk — коефіцієнт зсуву Σ ∈ Rk×k — коваріаційна матриця (додатноозначена матриця) |
| Носій функції | x ∈ μ + span(Σ) ⊆ Rk |
| Розподіл імовірностей |
існує лише за умови, що Σ є додатньоозначена матриця |
| Функція розподілу ймовірностей (cdf) | (не має аналітичного виразу) |
| Середнє | μ |
| Мода | μ |
| Дисперсія | Σ |
| Ентропія | |
| Твірна функція моментів (mgf) | |
| Характеристична функція | |
Позначення і параметризація
Багатовимірний нормальний розподіл k-вимірного вектору випадкових величин X = [X1, X2, …, Xk]T може записуватися у формі наступної нотації:
або із метою явно зазначити, що X є k-вимірним:
із k-вимірним вектором середніх значень
Визначення
Випадковий вектор має багатомірний нормальний розподіл, якщо виконується одне з наступних еквівалентних умов:
- Довільна лінійна комбінація компонентів вектора має нормальний розподіл є константою.
- Існує вектор незалежних стандартних нормальних випадкових величин , дійсний вектор і матриця розмірності , такі що:
- .
- Існує вектор і додатньо визначена симетрична матриця розмірності , такі що характеристична функція вектора має вид:
- .
Зауваження
- Якщо розглядати тільки розподілу з невиродженою коваріаційною матрицею, то еквівалентним буде також наступне визначення:
- Існує вектор і додатно визначена симетрична матриця розмірності , такі що щільність ймовірності вектора має вид:
- ,
- де — визначник матриці , а — матриця зворотна до
- Вектор є вектором середніх значень , а — його коваріаційна матриця
- У випадку , багатовимірний нормальний розподіл зводиться до звичайного нормального розподілу.
- Якщо випадковий вектор має багатовимірний нормальний розподіл, то пишуть .
Властивості
- Якщо вектор має багатовимірний нормальний розподіл, то його компоненти мають одновимірний нормальний розподіл. Зворотне, узагалі говорячи, невірно (див. приклад )!
- Якщо випадкові величини мають одномірний нормальний розподіл і спільно незалежні, те випадковий вектор має багатомірний нормальний розподіл. Матриця коваріацій такого вектора діагональна.
- Якщо має багатомірний нормальний розподіл, і його компоненти попарно некорельовані, то вони незалежні. Однак, якщо тільки компоненти мають одномірний нормальний розподіл і попарно не корелюють, те звідси не випливає, що вони незалежні.
- Контрприклад. Нехай , а з рівними ймовірностями. Тоді якщо , те кореляція і дорівнює нулю. Однак, ці випадкові величини залежні.
- Багатомірний нормальний розподіл стійко щодо лінійних перетворень. Якщо , а — довільна матриця розмірності , то
- .
Функція густини
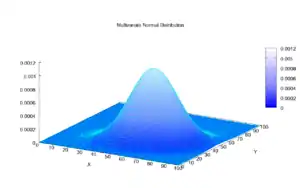
Не вироджений випадок
Багатовимірний нормальний розподіл називають "не виродженим" коли його симетрична матриця коваріацій є додатньоозначеною. В такому випадку розподіл має функцію густини:[1]
де це k-вимірний вектор стовпець дійсних чисел і це детермінант для . Вищенаведене рівняння спрощується до аналогічного рівняння, що відповідає одновимірному нормальному розподілу якщо є матрицею розміром (тобто єдиним дійсним числом).
Циркулярно-симетрична версія комплексного нормального розподілу має дещо відмінну форму.
Кожен окіл ізо-густини—окіл точок в k-вимірному просторі, в кожній з яких буде деяке стале значення густини —є еліпсом або його узагальненням для більших вимірів; оскільки багатовимірний нормальний розподіл є особливим випадком еліптичних розподілів.
В описовій статистиці відомо як відстань Махаланобіса, яка задає відстань обраної точки від середнього . Зауважте, що у випадку коли , розподіл зводиться до одновимірного нормального розподілу, і відстань Махаланобіса зводиться до абсолютного значення стандартної оцінки.
Біваріативний випадок
У 2-вимірному несингулярному випадку (k = rank(Σ) = 2), функція густини імовірності для вектору [X Y]′ є наступною:
де ρ — кореляція між X і Y і де і . В такому випадку,
У біваріативному випадку, перша еквівалентна умова встановлення нормальності багатовимірного розподілу може бути менш сувора: для того, щоб зробити висновок чи є вектор [X Y]′ біваріативно нормальним достатньо перевірити чи зліченно велика кількість відмінних лінійних комбінацій X і Y є нормально розподілені.[2]
Біваріативні околи ізо-густини на площині x,y є еліпсами. Із збільшенням абсолютного значення коефіцієнту кореляції ρ, ці околи будуть сплющуватися до наступної прямої :
Це пояснюється тим, що якщо в даному виразі sgn(ρ) замінити на ρ, воно є найкращим лінійним незміщеним передбаченням для Y, що задане значенням X.[3]
Багатомірна центральна гранична теорема
Нехай — послідовність незалежних і однаково розподілених випадкових векторів, кожний з який має середнє і невироджену матрицю коваріацій . Позначимо через вектор часткових сум. Тоді при має місце збіжність розподілів векторів , де має розподіл . В умовах багатовимірної центральної граничної теореми розподіл будь-яких неперервних функцій збігається до розподілу . Як нам буде потрібна тільки .
Наслідок
В умовах багатовимірної центральної граничної теореми має місце збіжність .
Примітки
- UIUC, Lecture 21. The Multivariate Normal Distribution, 21.5:"Finding the Density".
- Hamedani, G. G.; Tata, M. N. (1975). On the determination of the bivariate normal distribution from distributions of linear combinations of the variables. The American Mathematical Monthly 82 (9): 913–915. doi:10.2307/2318494.
- Wyatt, John. Linear least mean-squared error estimation. Lecture notes course on applied probability. Процитовано 23 січня 2012.