Комутативна діаграма

У математиці, та особливо в теорії категорій, комутативна діаграма — зображувана в наочному вигляді структура на кшталт графу, вершинами якої служать об'єкти певної категорії, а ребрами — морфізм. Комутативність означає, що для будь-яких вибраних початкового та кінцевого об'єкта, для орієнтованих шляхів, які поєднують їх, композиція відповідних шляху морфізмів не залежатиме від вибору шляху. Крім власне теорії категорій, комутативні діаграми незамінні в алгебричній геометрії та застосовуються в багатьох інших сучасних галузях математики.

Приклади

У прикладі, що ілюструє першу теорему про ізоморфізми, комутативність діаграми значить рівно те, що $f={\tilde {f}}\circ \pi$ :

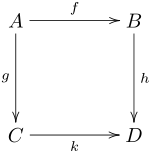
Для комутативного прямокутника комутативність означає незалежність вибору шляху: $h\circ f=k\circ g$

Позначки

В алгебрі різні типи морфізмів позначаються різніми стрілками: $\rightarrow$ просто морфізм; $\hookrightarrow$ мономорфізм, $\twoheadrightarrow$ епіморфізм, ${\overset {\sim }{\rightarrow }}$ ізоморфізм. Пунктирна стрілка зазвичай позначає шуканий морфізм (тоді як суцільні стрілки задані з самого спочатку). Мається на увазі, що якщо існує шлях для морфізма (позначених суцільними лініями), що з'єднує початок та кінець шуканого морфізма, то він існує та визначається з властивостей комутативності діаграми.

Див. також

Точна послідовність

Посилання

Діаграми в MathWorld.
WildCats Теорія категорій в пакеті Математика. Перетворення та візуалізація об'єктів, морфізма, категорії, функторів, природні перетворення.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.