Нуль в нульовому степені
Вираз (нуль в нульовому степені) багато підручників вважають невизначеним і позбавленим сенсу[1]. Пов'язано це з тим, що функція двох змінних в точці має неусувний розрив. Справді, уздовж додатного напрямку осі де вона дорівнює одиниці, а вздовж додатного напрямку осі де вона дорівнює нулю. Тому ніяка домовленість про значення не може дати неперервну в нулі функцію.
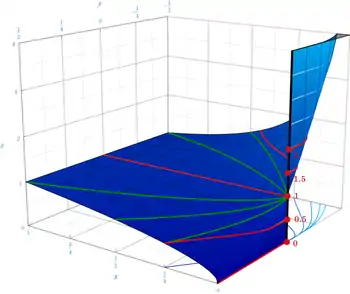
Деякі автори пропонують домовитись про те, що цей вираз дорівнює 1. На користь такого варіанту наводяться кілька доводів. Наприклад, розклад у ряд експоненти:
можна записати коротше, якщо прийняти :
(наша домовленість використовується при ).
Якщо 0 відносити до натуральних чисел, то піднесення до натурального степеня можна визначити так:
і тоді піднесення будь-якого числа (зокрема й нуля) до нульового степеня даватиме 1.
Інше обґрунтування домовленості спирається на «Теорію множин» Бурбакі[2]: число різних відображень n -елементної множини в m-елементну дорівнює при отримуємо відображення порожньої множини в порожню, а воно єдине. Зрозуміло, це не можна вважати доведенням (домовленості не потребують доведень), тим більше що в самій теорії множин домовленість не використовується.
В будь-якому випадку домовленість чисто символічна, і вона не може використовуватися ні в алгебраїчних, ні в аналітичних перетвореннях через розривність функції в цій точці. Приклад для аналітичних обчислень: вираз де — довільне додатне дійсне число. При ми отримуємо невизначеність типу і, якщо не відрізняти граничну форму (де кожен з нулів позначає прямування до нуля) і значення (де кожен з нулів і є нуль), можна помилково порахувати, що границя дорівнює 1. Насправді цей вираз тотожно дорівнює Це означає, що нескінченно мала в нескінченно малому степені може в границі дати будь-яке значення, не обов'язково одиницю. Подібних помилок можна припуститися, якщо використовувати домовленість в алгебричних перетвореннях.
Історія різних точок зору
Дискусія з приводу визначення триває, принаймні, з початку XIX століття. Багато математиків тоді приймали цю угоду, але в 1821 році Коші[3] відніс до невизначеностей, таких, як У 1830-х роках Лібрі[4][5] опублікував непереконливий аргумент на користь (див. Функція Гевісайда § Історія), і Мебіус[6] став на його сторону, помилково заявивши, що щоразу, коли . Оглядач, який підписався просто як «S», надав контрприклад , і це трохи заспокоїло дебати. Більше історичних деталей можна знайти в книзі Кнута (1992)[7] .
Пізніші автори інтерпретують описану вище ситуацію по-різному. Деякі стверджують, що оптимальне значення для залежить від контексту, і тому визначити його раз і назавжди проблематично[8]. Згідно з Бенсоном (1999), «вибір, чи слід визначати ґрунтується на зручності, а не на правильності. Якщо ми утримаємося від визначення , то деякі твердження стають надмірно незручними. <…> Консенсус полягає у використанні визначення , хоча є підручники, які утримуються від визначення »[9].
Частина математиків вважає, що має бути визначено як 1. Наприклад, Кнут (1992) впевнено стверджує, що «має бути 1», розрізняючи значення , яке має дорівнювати 1, як це було запропоновано Лібрі, і граничну форму (абревіатура для границі де ), яка обов'язково є невизначеністю, як зазначено Коші: «І Коші, й Лібрі мали рацію, але Лібрі та його захисники не розуміли, чому істина на їхньому боці»[7].
Авторитетний сайт MathWorld, навівши думку Кнута, все ж констатує, що зазвичай значення вважається невизначеним, незважаючи на те, що домовленість дозволяє в деяких випадках спростити запис формул[10]. Велика радянська енциклопедія та деякі інші джерела характеризують як вираз, що не має сенсу (невизначеність).
Розкриття невизначеності 00
Якщо дано дві функції і , які прямують до нуля, то границя в загальному випадку може бути будь-якою, таким чином, з цієї точки зору є невизначеністю. Для знаходження границі в цьому випадку користуються методами розкриття невизначеності, як правило спочатку взявши логарифм від цього виразу: , а потім скориставшись правилом Лопіталя.
Однак, за певних умов ця границя буде завжди дорівнювати одиниці. А саме: якщо функції і є аналітичними в точці (тобто в деякому околі точки збігаються зі своїм рядом Тейлора), і , а в околі , то границя при яке прямує до нуля справа дорівнює 1[11][12][13].
Наприклад, таким чином можна відразу переконатися, що
При цьому треба не забувати, що якщо хоча б одна з функцій не розкладається в ряд Тейлора в точці 0, то границя може бути будь-якою, або її може не існувати. Наприклад,
У комп'ютерах
Стандарт IEEE 754-2008, що описує формат подання чисел з рухомою комою, визначає три функції піднесення до степеня[14]:
- Функція для піднесення до цілого степеня: . Відповідно до стандарту, для будь-якого , зокрема, коли дорівнює нулю,
NaNабо нескінченності. - Функція для піднесення до довільного степеня: — по суті рівна . Відповідно до стандарту, повертає значення «не числ»
NaN. - Функція для піднесення до довільного степеня, яка особливо визначена для цілих чисел: . Відповідно до стандарту, для всіх (так само як і ).
У багатьох мовах програмування нуль в нульовому степені дорівнює 1. Наприклад, в C++: pow(0, 0) == 1, у мові Haskell це правильно для всіх трьох стандартних операцій піднесення до степеня: 0^0 == 1, 0^^0 == 1, 0**0 == 1.
Література
- Степенная функция // Большая советская энциклопедия : в 30 т. / главн. ред. А. М. Прохоров. — 3-е изд. — М. : «Советская энциклопедия», 1969—1978. (рос.)
Примітки
- БСЭ, 1969—1978.
- N. Bourbaki. Theory of Sets // Elements of Mathematics, Springer-Verlag, 2004, III, § 3.5.
- Augustin-Louis Cauchy. Cours d'Analyse de l'École Royale Polytechnique (1821). In his Oeuvres Complètes, series 2, volume 3.
- Guillaume Libri. Note sur les valeurs de la fonction 00x, Journal für die reine und angewandte Mathematik 6 (1830), 67-72.
- Guillaume Libri. Mémoire sur les fonctions discontinues, Journal für die reine und angewandte Mathematik 10 (1833), 303—316.
- A. F. Möbius. // Journal für die reine und angewandte Mathematik : magazin. — 1834. — S. 134—136.
- Donald E. Knuth, Two notes on notation, Amer. Math. Monthly 99 no. 5 (May 1992), 403—422 (arXiv: math/9205211 [math.HO]).
- Например: Edwards and Penny (1994). Calculus, 4th ed, Prentice-Hall, p. 466; Keedy, Bittinger, and Smith (1982). Algebra Two. Addison-Wesley, p. 32.
- Donald C. Benson, The Moment of Proof: Mathematical Epiphanies. New York Oxford University Press (UK), 1999. ISBN 978-0-19-511721-9.
- Weisstein, Eric W.. Power. Wolfram MathWorld. Процитовано 5 жовтня 2018.
- Louis M. Rotando; Henry Korn. The indeterminate form 00 // Mathematics Magazine : magazine. — 1977. — No. 1 (1). — P. 41—42.
- sci.math FAQ: What is 0^0?. www.faqs.org. Процитовано 30 серпня 2019.
- Leonard J. Lipkin. On the Indeterminate Form 00 // The College Mathematics Journal. — 2003. — Вип. 1. — С. 55—56. — ISSN 0746-8342.
- IEEE Computer Society. . — IEEE, 2008. — 8. — ISBN 978-0-7381-5753-5.