Осцилятор Ван дер Поля

Фазові траєкторії двовимірної системи при різних значеннях параметра ${\displaystyle \mu }$.

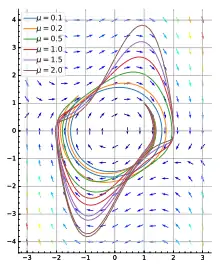
Коли ${\displaystyle \mu >0}$, нульовий розв'язок системи нестійкий. За допомогою теореми Ліенара можна довести що система має стійкий граничний цикл. Нехай ${\displaystyle y={\dot {x}}}$, тоді систему можна записати у двовимірному просторі як[1]

${\displaystyle {\dot {x}}=y}$

${\displaystyle {\dot {y}}=\mu (1-x^{2})y-x,}$

або, якщо взяти ${\displaystyle y=x-x^{3}/3-{\dot {x}}/\mu }$,

${\displaystyle {\dot {x}}=\mu \left(x-{\frac {1}{3}}x^{3}-y\right)}$

${\displaystyle {\dot {y}}={\frac {1}{\mu }}x.}$

Детермінований хаос в системі Ван дер Поля з вимушеним коливанням. Параметр нелінійного загасання ${\displaystyle \mu =8.53}$, амплітуда ${\displaystyle A=1.2}$, кутова швидкість ${\displaystyle \omega =2\pi /10}$.

Осцилятор Ван дер Поля з вимушеними коливаннями під впливом зовнішньої періодичної сили можна записати наступним чином

${\displaystyle {d^{2}x \over dt^{2}}-\mu (1-x^{2}){dx \over dt}+x-A\sin(\omega t)=0,}$

де ${\displaystyle A}$ задає амплітуду, а ${\displaystyle \omega }$ кутову швидкість.

Осцилятор був вперше досліджений голландським фізиком Балтазаром Ван дер Полом та був названий на його честь.

Рівняння Ліенара, назване на честь французького інженера Альфред-Марі Ліенара, є узагальненням системи Ван дер Поля.