Граничний цикл

Перший приклад (нестікого) граничного циклу (Пуанкаре, 1882).[1]

Стійкий граничний цикл в системі Ван дер Поля (${\displaystyle \mu =1}$).

Напівстійкий граничний цикл.

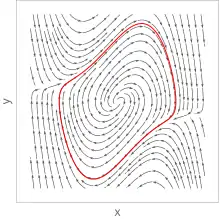
Розглянемо двовимірну автономну систему звичайних диференціальних рівнянь:

${\displaystyle {\dot {x}}=f(x),}$

де ${\displaystyle f:\mathbb {R} ^{2}\to \mathbb {R} ^{2}}$ гладка функція. Розв'язок цієї системи ${\displaystyle x(t)}$ заданий гладкою функцією ${\displaystyle x:\mathbb {R} \to \mathbb {R} ^{2}}$ яка задовольняє систему диференціальних рівнянь. Траєкторія називається замкнутою, або періодичною, якщо розв'язок, з початковими умовами ${\displaystyle x(0)=x_{0}\in \mathbb {R} ^{2}}$, є (не сталою) періодичною функцією, тобто існує час ${\displaystyle \tau >0}$ після якого система повертається до початкової точки (${\displaystyle \forall t\in \mathbb {R} .~x(t+\tau )=x(t)}$).

Граничний цикл — замкнута траєкторія у фазовому просторі двовимірної динамічної системи, до якої збігається хоча б одна фазова траєкторія при ${\displaystyle t\rightarrow \infty }$ або при ${\displaystyle t\rightarrow -\infty }$. Граничний цикл називається:[2]

• Стійким якщо траєкторії збігаються до замкнутої кривої по спіралі з обох боків при ${\displaystyle t\rightarrow \infty }$.
• Нестійким якщо траєкторії збігаються до замкнутої кривої по спіралі з обох боків при ${\displaystyle t\rightarrow -\infty }$.
• Напівстійким якщо траєкторії збігаються до замкнутої кривої по спіралі при ${\displaystyle t\rightarrow \infty }$ з одного боку та при ${\displaystyle t\rightarrow -\infty }$ з іншого, або навпаки.

Перший відомий приклад граничного циклу належить Пуанкаре, та був продемонстрований в 1882 році за допомогою наступної автономної системи [1] :

${\displaystyle {\dot {x}}=x(x^{2}+y^{2}-1)-y(x^{2}+y^{2}+1),}$

${\displaystyle {\dot {y}}=y(x^{2}+y^{2}-1)+x(x^{2}+y^{2}+1).}$

Ця система має нестійкий граничний цикл на одиничному колі у фазовому просторі, тобто на множині яка задовольняє алгебричне рівняння ${\displaystyle x^{2}+y^{2}=1}$. На відміну від цього, в інших (навіть алгебричних) системах граничні цикли подекуди не можуть бути записаними за допомогою алгебричних рівнянь. Прикладом системи з токою властивістью є осцилятор Ван дер Поля:

${\displaystyle {\dot {x}}=y,}$

${\displaystyle {\dot {y}}=\mu (1-x^{2})y-x,}$

зі стійким граничним циклом (при параметрі нелінійного згасання ${\displaystyle \mu >0}$) який не має алгебричного виразу.[3]

Заради прикладу напівстійкого граничного циклу можна розглянути наступну систему:

${\displaystyle {\dot {x}}=-y+x(-1+x^{2}+y^{2})^{2},}$

${\displaystyle {\dot {y}}=x+y(-1+x^{2}+y^{2})^{2}.}$

Напівстійкий граничний цикл цієї системи також лежить на одиничному колі.

В загальному випадку, доведення існування граничного циклу є нетривіальною проблемою. Існують деякі критерії існування (на пр. Теорема Пуанкаре — Бендиксона) та неіснування граничних циклів (на пр. критерій Бендиксона — Дюлака), однак всі вони дають лише достатні умови.

Друга частина Шістнадцятої проблеми Гільберта.

• Гранична точка
• Гранична множина
• Атрактор
• Теорема Пуанкаре — Бендиксона
• Критерій Бендиксона — Дюлака