Перетворення Радона

В математиці перетворення Радона — це інтегральне перетворення, яке переводить функцію f, визначену на площині, в функцію Rf, визначену на (двовимірному) просторі з прямих на площині, значення якої у певній прямій дорівнює криволінійному інтегралу від цієї функції над цією прямою.

Перетворення Радона. Карти f на (x, y) -область Rf на (α, з) -область.

Перетворення Радона для характеристичної функції двох квадратів, зображених на малюнку нижче. Більш світлі області вказують на більші значення функцій. Чорний колір позначає нуль.

Початкова функція дорівнює одиниці на білій області і нулю в темній області.

Перетворення було введене в 1917 році Йоганом Радоном[1] який також надав формулу зворотного перетворення. Крім того, Радон визначив формули для перетворення в трьох вимірах, в яких інтегрування відбувається на площині (інтегрування по лініях відоме як рентгенівське перетворення). Пізніше це було узагальнено до евклідових просторів більш високого розміру, а ширше — в контексті інтегральної геометрії. Комплексний аналог перетворення Радона відомий як перетворення Пенроуза. Перетворення Радона широко застосовується для томографії, створення зображення з проекційних даних, пов'язаних із скануванням поперечного перерізу об'єкта.

Пояснення

Якщо функція $f$ представляє невизначену щільність, тоді перетворення Радона представляє дані проекції, отримані як вихід томографічного сканування. Отже, зворотне перетворення Радона може бути використане для реконструкції початкової щільності з даних проекції, і таким чином воно формує математичну основу томографічної реконструкції, також відому як ітеративна реконструкції.

Дані про перетворення Радона часто називають синограмою, оскільки перетворення Радона в центрі точкового джерела є синусоїдою. Отже, перетворення Радона для ряда дрібних предметів графічно постає як кількість розмитих синусоїд з різними амплітудами та фазами.

Перетворення Радона корисна при комп'ютерній томографії (КВТ-сканування), також застосовується у сканерах штрих-кодів, електронній мікроскопії, макромолекулярних зборах, таких як віруси та білкові комплекси, рефлекторній сейсмології та при вирішенні гіперболічних часткових диференціальних рівнянь.

Визначення

Нехай ƒ(x) = ƒ(x, y) — функція, яка задовольняє трьом умовам регулярності[2]:

ƒ(x, y) — неперервна
подвійний інтеграл $\int \int {\frac {|f(x,y)|}{\sqrt {x^{2}+y^{2}}}}dxdy$ , що визначений на всій площині, збігається
для будь-якої довільної точки $(x,y)$ на площині виконується, що $\lim _{r\to \infty }\int _{0}^{2\pi }f(x+r\cos \phi ,y+r\sin \phi )d\phi =0$

Перетворення Радона, Rƒ, є функцією, визначеною на просторі прямих L в просторі R² криволінійно інтегрованою вздовж кожної такої прямої, як

Rf(L)=\int _{L}f(\mathbf {x} )\,|d\mathbf {x} |.

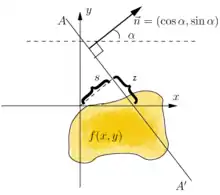
Конкретніше, параметризацію будь-якої прямої L щодо довжини дуги z завжди можна записати як

(x(z),y(z))={\Big (}(z\sin \alpha +s\cos \alpha ),(-z\cos \alpha +s\sin \alpha ){\Big )}\,

де s — відстань L від початку і $\alpha$ — кут, який нормальний до L вектор утворює з віссю х. Звідси випливає, що величини (α, s) можна вважати координатами на просторі всіх ліній в R², а перетворення Радона в цих координатах визначають як

{\begin{aligned}Rf(\alpha ,s)&=\int _{-\infty }^{\infty }f(x(z),y(z))\,dz\\&=\int _{-\infty }^{\infty }f{\big (}(z\sin \alpha +s\cos \alpha ),(-z\cos \alpha +s\sin \alpha ){\big )}\,dz\end{aligned}}

Більш загальне визначення

Нехай $f$ - функція на $\mathbb {R} ^{n}$ , інтегровувана по кожній гіперплощині. Нехай також $\mathbb {P} ^{n}$ простір усіх гіперплощин у $\mathbb {R} ^{n}$ , наділене відповідною топологією. Перетворення Радона функції $f$ визначається як функція ${\hat {f}}$ на $\mathbb {P} ^{n}$ , і задається формулою

${\hat {f}}(\xi )=\int _{\xi }f(x)dm(x),$

де $dm$ - евклідова міра на гіперплощині $\xi .$

Гіперплощину $\xi \in \mathbb {P} ^{n}$ можна записати у вигляді $\xi =\{x\in \mathbb {P} ^{n}\,|\,(x,\omega )=p\},$ де $(\cdot ,\cdot )$ - звичайний скалярний добуток, $\omega =(\omega _{1},...,\omega _{n})$ - одиничний вектор та $p\in \mathbb {R} .$ Пари $(\omega ,p)$ та $(-\omega ,-p)$ приводять до однієї і тої самої гіперплощини ${\displaystyle \xi$ відображення $(\omega ,\pi )\rightarrow \xi$ є двократне накриття $\mathbb {S} ^{n-1}\times \mathbb {R}$ на $\mathbb {P} ^{n}$ . Таким чином, простір $\mathbb {P} ^{n}$ має канонічну структуру многовиду, відносно якої це накриваюче відображення диференційовуване й регулярне[3].

Зв'язок з перетворенням Фур'є

Обчислення двовимірного перетворення Радона через два перетворення Фур'є.

Перетворення Радона тісно пов'язане з перетворенням Фур'є. Ми визначаємо тут універсальне перетворення Фур'є як

{\hat {f}}(\omega )=\int _{-\infty }^{\infty }f(x)e^{-2\pi ix\omega }\,dx.

і для функції для 2-х векторів $\mathbf {x} =(x,y)$ ,

{\hat {f}}(\mathbf {w} )=\int \limits _{-\infty }^{\infty }\int \limits _{-\infty }^{\infty }f(\mathbf {x} )e^{-2\pi i\mathbf {x} \cdot \mathbf {w} }\,dx\,dy.

Для зручності позначте ${\mathcal {R}}_{\alpha }[f](s)={\mathcal {R}}[f](\alpha ,s)$ . Тоді теорема Фур'є про зріз функції констатує

{\widehat {{\mathcal {R}}_{\alpha }[f]}}(\sigma )={\hat {f}}(\sigma \mathbf {n} (\alpha ))

де

\mathbf {n} (\alpha )=(\cos \alpha ,\sin \alpha ).

Таким чином, двовимірне перетворення Фур'є початкової функції вздовж лінії під кутом нахилу $\alpha$ — це перетворення Фур'є для однієї змінної над перетворенням Радона (отримане під кутом нахила $\alpha$ ) цієї функції. Цей факт може бути використаний для обчислення як перетворення Радона, так і зворотньої функції.

Результат можна узагальнити для n-мірного випадку

{\hat {f}}(r\alpha )=\int _{-\infty }^{\infty }{\mathcal {R}}f(\alpha ,s)e^{-2\pi isr}\,ds.

Подвійне перетворення

Подвійне перетворення Радона є своєрідним примиканням до перетворення Радона. Починаючи з функції g на просторі Σ_n, подвійне перетворення Радона — функція ${\mathcal {R}}^{*}g$ на Rⁿ, яка визначається в такий спосіб

{\mathcal {R}}^{*}g(x)=\int _{x\in \xi }g(\xi )\,d\mu (\xi ).

Інтеграл тут береться за множину всіх гіперплощин, що проходять через точку х ∈ Rⁿ, а міра d є унікальною мірою ймовірності на множині $\{\xi |x\in \xi \}$ є інваріантом при обертанні навколо точки x.

Конкретно, для двовимірного перетворення Радона подвійне перетворення задається таким чином

{\mathcal {R}}^{*}g(x)={\frac {1}{2\pi }}\int _{\alpha =0}^{2\pi }g(\alpha ,\mathbf {n} (\alpha )\cdot \mathbf {x} )\,d\alpha .

У контексті обробки зображень подвійне перетворення зазвичай називають зворотньою проекцією[4] оскільки воно приймає функцію, визначену в кожній лінії в площині, і «розмазує» або проектує її назад по лінії для створення зображення.

Переплетення власності

Нехай Δ позначає оператор Лапласа на R ⁿ:

\Delta ={\frac {\partial ^{2}}{\partial x_{1}^{2}}}+\cdots +{\frac {\partial ^{2}}{\partial x_{n}^{2}}}.

Це природний обертальний інваріантний диференціальний оператор другого порядку. На Σ_n, «радіальна» друга похідна

Lf(\alpha ,s)\equiv {\frac {\partial ^{2}}{\partial s^{2}}}f(\alpha ,s)

також інваріантна відносно обертання. Перетворення Радона та його подвійний є переплетеними операторами для цих двох диференціальних операторів у тому сенсі, що[5]

{\mathcal {R}}(\Delta f)=L({\mathcal {R}}f),\quad {\mathcal {R}}^{*}(Lg)=\Delta ({\mathcal {R}}^{*}g).

Аналізуючи рішення хвильового рівняння в декількох просторових вимірах, властивість переплетення призводить до поступального представлення Лакса і Філіпса[6]. У візуалізації[7] та чисельному аналізі[8] це використовується для зменшення багатовимірних задач на одновимірні, як метод розмірного розщеплення.

Підходи до реконструкції

Процес реконструкції створює зображення (або функцію $f$ у попередньому розділі) з його проекційних даних. Реконструкція — обернена задача.

Формула інверсії радону

У двовимірному випадку найбільш часто використовується аналітична формула для відновлення $f$ знаючи його перетворення Радона за допомогою формули відфільтрованої зворотньої проекції або формули інверсії Радона:

f(\mathbf {x} )=\int _{0}^{\pi }({\mathcal {R}}f(\cdot ,\theta )*h)(\left\langle \mathbf {x} ,\mathbf {n} _{\theta }\right\rangle )d\theta

[9]

де $h$ таке, що ${\hat {h}}(k)=|k|$ [10].

Ядро згортки $h$ в деякій літературі згадується як фільтр Рампа.

Нерегулярна похибка

Інтуїтивно, у відфільтрованій формулі зворотного проектування, за аналогією з диференціацією, для якої $\left({\widehat {{\frac {d}{dx}}f}}\right)\!(k)=ik{\widehat {f}}(k)$ , ми бачимо, що фільтр виконує операцію, аналогічну операції взяття похідної. Грубо кажучи, тоді фільтр робить об'єкти більш сингулярними.

Кількісне твердження про нерегулярну похибку радонової інверсії полягає в наступному: Ми маємо ${\widehat {{\mathcal {R}}^{*}{\mathcal {R}}g}}(k)={\frac {1}{||\mathbf {k} ||}}{\hat {g}}(\mathbf {k} )$

де ${\mathcal {R}}^{*}$ є раніше визначеним примиканням до Радонового перетворення.

Таким чином для $g(\mathbf {x} )=e^{i\left\langle \mathbf {k} _{0},\mathbf {x} \right\rangle }$ ,

{\mathcal {R}}^{*}{\mathcal {R}}g={\frac {1}{||\mathbf {k_{0}} ||}}e^{i\left\langle \mathbf {k} _{0},\mathbf {x} \right\rangle }

.

Складний показник $e^{i\left\langle \mathbf {k} _{0},\mathbf {x} \right\rangle }$ таким чином, є власною функцією ${\mathcal {R}}^{*}{\mathcal {R}}$ із власним значенням ${\frac {1}{||\mathbf {k_{0}} ||}}$ . Таким чином, сингулярні значення ${\mathcal {R}}$ є ${\sqrt {\frac {1}{||\mathbf {k} ||}}}$ . Оскільки ці особливі значення мають прямувати до 0, ${\mathcal {R}}^{-1}$ є необмеженим. [10]

Ітеративні методи реконструкції

Порівняно з методом відфільтрованого зворотного проектування, ітеративна реконструкція коштує великих витрат на обчислення, обмежуючи її практичне використання. Однак через недоброзичливість інверсії радону метод фільтруваної зворотньої проекції може виявитися нездійсненним при наявності розриву або шуму. Методи ітеративної реконструкції (наприклад, ітеративна розріджена асимптотична мінімальна різниця[11]) можуть забезпечити зменшення артефактів металу, зменшення шуму та дози для реконструкції результату, що привертає великий науковий інтерес по всьому світу.

Формули інверсії

Явні та обчислювально ефективні формули інверсії для перетворення Радона та його подвійності. Перетворення Радона в n розмірах може бути інвертованим формулою[12]

c_{n}f=(-\Delta )^{(n-1)/2}R^{*}Rf\,

де

c_{n}=(4\pi )^{(n-1)/2}{\frac {\Gamma (n/2)}{\Gamma (1/2)}}.

а потужність Лаплаціана (−Δ)^(n−1)/2 визначається як псевдодиференціальний оператор або, при необхідності, перетворенням Фур'є

\left[{\mathcal {F}}(-\Delta )^{(n-1)/2}\phi \right](\xi )=|2\pi \xi |^{n-1}({\mathcal {F}}\phi )(\xi ).

Для обчислювальних цілей, потужність Лаплаціани змішується з подвійним перетворенням R^*, щоб отримати[13]

c_{n}f={\begin{cases}R^{*}{\frac {d^{n-1}}{ds^{n-1}}}Rf&n{\rm {\ odd}}\\R^{*}H_{s}{\frac {d^{n-1}}{ds^{n-1}}}Rf&n{\rm {\ even}}\end{cases}}

де H_s — перетворення Гільберта відносно змінної s. У двох вимірах оператор H_sd/ds з'являється в обробці зображень як рамповий фільтр[14]. Можна легко довести з теореми Фур'є про зріз і зміни змінних для інтеграції, що для компактно підтримуваної безперервної функції ƒ для двох змінних

через

f={\frac {1}{2}}R^{*}H_{s}{\frac {d}{ds}}Rf.

Таким чином, в контексті обробки зображень вихідне зображення ƒ може бути відновлено з даних «синограми» Rƒ шляхом застосування рампового фільтру (у $s$ змінній), а потім зворотнього проектування. Оскільки етап фільтрації може бути виконаний ефективно (наприклад, використовуючи методи цифрової обробки сигналу), а один крок зворотнього проектування є просто накопиченням значень у пікселях зображення, що призводить до високоефективного, а отже, широко використовуваного алгоритму.

Явна формула інверсії, отримана останнім методом[4]

f(x)={\frac {1}{2}}(2\pi )^{1-n}(-1)^{(n-1)/2}\int _{S^{n-1}}{\frac {\partial ^{n-1}}{\partial s^{n-1}}}Rf(\alpha ,\alpha \cdot x)\,d\alpha

якщо n непарне, і

f(x)=(2\pi )^{-n}(-1)^{n/2}\int _{-\infty }^{\infty }{\frac {1}{q}}\int _{S^{n-1}}{\frac {\partial ^{n-1}}{\partial s^{n-1}}}Rf(\alpha ,\alpha \cdot x+q)\,d\alpha \,dq

якщо n парне.

Подвійне перетворення також може бути обернено аналогічною формулою:

c_{n}g=(-L)^{(n-1)/2}R(R^{*}g).\,

Перетворення Радона в алгебричній геометрії

В алгебраїчній геометрії перетворення Радона (також відоме як перетворення Брилінського-Радона) будується наступним чином.

Пишуть

\mathbf {P} ^{d}{\stackrel {p_{1}}{\gets }}H{\stackrel {p_{2}}{\to }}\mathbf {P} ^{\vee ,d}

для універсальної гіперплощини, тобто H складається з пар (x, h), де x — точка в d-вимірному проективному просторі $\mathbf {P} ^{d}$ і h — точка у подвійному проекційному просторі (іншими словами, x є лінією через початок у (d+1)-вимірному афінному просторі, а h — гіперплощина у цьому просторі), такий, що x міститься в h.

Тоді перетворення Брилінкського — Радона є функтором між відповідними похідними категоріями еталевих пучків

Rad:=Rp_{2,*}p_{1}^{*}:D(\mathbf {P} ^{d})\to D(\mathbf {P} ^{\vee ,d}).

Основна теорема про це перетворення полягає в тому, що це перетворення проектує еквівалентність категорій перекручених пучків на проективному просторі та його подвійному проективному просторі аж до постійних пучків[15].

Застосування

Рентгенівська трансформація є найбільш широко використовуваним особливим випадком цієї конструкції, і її отримують шляхом інтеграції з прямими лініями.

Див. також

Періодограма
Відповідний фільтр
Деконволюція
Рентгенівська трансформація
Функція перетворення
Перетворення Хаффа, коли воно пишеться у безперервній формі, дуже схоже, якщо не еквівалентне, перетворенню Радона. [16]
Теорема Коші-Крофтона є тісно пов'язаною формулою для обчислення довжини кривих у просторі.
Швидке перетворення Фур'є

Примітки

Radon, 1917.
Radon, J. (December 1986). On the determination of functions from their integral values along certain manifolds. IEEE Transactions on Medical Imaging 5 (4): 170–176. PMID 18244009. doi:10.1109/TMI.1986.4307775.
S.Helgason - The Radon transform.
Roerdink, 2001.
Helgason, 1984, Lemma I.2.1.
Lax, P. D.; Philips, R. S. (1964). Scattering theory. Bull. Amer. Math. Soc. 70: 130–142. doi:10.1090/s0002-9904-1964-11051-x.
Bonneel, N.; Rabin, J.; Peyre, G.; Pfister, H. (2015). Sliced and Radon Wasserstein Barycenters of Measures. Journal of Mathematical Imaging and Vision 51: 22–25. doi:10.1007/s10851-014-0506-3.
Rim, D. (2018). Dimensional Splitting of Hyperbolic Partial Differential Equations Using the Radon Transform. SIAM J. Sci. Comput. 40: A4184–A4207. arXiv:1705.03609. doi:10.1137/17m1135633.
Candès, 2016a.
Candès, 2016b.
Abeida, Habti; Zhang, Qilin; Li, Jian; Merabtine, Nadjim (2013). Iterative Sparse Asymptotic Minimum Variance Based Approaches for Array Processing. IEEE Transactions on Signal Processing (IEEE) 61 (4): 933–944. Bibcode:2013ITSP...61..933A. ISSN 1053-587X. arXiv:1802.03070. doi:10.1109/tsp.2012.2231676.
Helgason, 1984, Theorem I.2.13.
Helgason, 1984, Theorem I.2.16.
Nygren, 1997.
Kiehl та Weissauer, (2001)
van Ginkel, Hendricks та van Vliet, 2004.

Список літератури

Radon, Johann (1917). Über die Bestimmung von Funktionen durch ihre Integralwerte längs gewisser Mannigfaltigkeiten. Berichte über die Verhandlungen der Königlich-Sächsischen Akademie der Wissenschaften zu Leipzig, Mathematisch-Physische Klasse [Reports on the proceedings of the Royal Saxonian Academy of Sciences at Leipzig, mathematical and physical section] (Leipzig: Teubner) (69): 262–277.; Translation: Radon, J.; Parks, P.C. (translator) (1986). On the determination of functions from their integral values along certain manifolds. IEEE Transactions on Medical Imaging 5 (4): 170–176. PMID 18244009. doi:10.1109/TMI.1986.4307775..
Hazewinkel, Michiel, ред. (2001). Перетворення Радона. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4..
Helgason, Sigurdur (1984). Groups and Geometric Analysis: Integral Geometry, Invariant Differential Operators, and Spherical Functions. Academic Press. ISBN 0-12-338301-3..
Candès, Emmanuel (2 лютого 2016a). Applied Fourier Analysis and Elements of Modern Signal Processing - Lecture 9.
Candès, Emmanuel (4 лютого 2016b). Applied Fourier Analysis and Elements of Modern Signal Processing - Lecture 10.
Nygren, Anders J. (1997). Filtered Back Projection. Tomographic Reconstruction of SPECT Data.
van Ginkel, M.; Hendricks, C.L. Luengo; van Vliet, L.J. (2004). A short introduction to the Radon and Hough transforms and how they relate to each other. Архів оригіналу за 29 липня 2016.

Подальше читання

Lokenath Debnath; Dambaru Bhatta (19 квітня 2016). Integral Transforms and Their Applications. CRC Press. ISBN 978-1-4200-1091-6.
Deans, Stanley R. (1983). The Radon Transform and Some of Its Applications. New York: John Wiley & Sons.
Helgason, Sigurdur (2008). Geometric analysis on symmetric spaces. Mathematical Surveys and Monographs 39 (вид. 2nd). Providence, R.I.: American Mathematical Society. ISBN 978-0-8218-4530-1. MR 2463854. doi:10.1090/surv/039.
Herman, Gabor T. (2009). Fundamentals of Computerized Tomography: Image Reconstruction from Projections (вид. 2nd). Springer. ISBN 978-1-85233-617-2.
Hazewinkel, Michiel, ред. (2001). Radon transform. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
Natterer, Frank (June 2001). The Mathematics of Computerized Tomography. Classics in Applied Mathematics 32. Society for Industrial and Applied Mathematics. ISBN 0-89871-493-1.
Natterer, Frank; Wübbeling, Frank (2001). Mathematical Methods in Image Reconstruction. Society for Industrial and Applied Mathematics. ISBN 0-89871-472-9.
Kiehl, Reinhardt; Weissauer, Rainer (2001). Weil conjectures, perverse sheaves and l'adic Fourier transform. Springer. ISBN 3-540-41457-6. MR 1855066. doi:10.1007/978-3-662-04576-3.

Посилання

Weisstein, Eric W. {{{title}}}(англ.) на сайті Wolfram MathWorld.
Analytical projection (the Radon transform) [video].

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[FOOTNOTERadon1917-1] Radon, 1917.

[2] Radon, J. (December 1986). On the determination of functions from their integral values along certain manifolds. IEEE Transactions on Medical Imaging 5 (4): 170–176. PMID 18244009. doi:10.1109/TMI.1986.4307775.

[3] S.Helgason - The Radon transform.

[FOOTNOTERoerdink2001-4] Roerdink, 2001.

[FOOTNOTEHelgason1984Lemma_I.2.1-5] Helgason, 1984, Lemma I.2.1.

[6] Lax, P. D.; Philips, R. S. (1964). Scattering theory. Bull. Amer. Math. Soc. 70: 130–142. doi:10.1090/s0002-9904-1964-11051-x.

[7] Bonneel, N.; Rabin, J.; Peyre, G.; Pfister, H. (2015). Sliced and Radon Wasserstein Barycenters of Measures. Journal of Mathematical Imaging and Vision 51: 22–25. doi:10.1007/s10851-014-0506-3.

[8] Rim, D. (2018). Dimensional Splitting of Hyperbolic Partial Differential Equations Using the Radon Transform. SIAM J. Sci. Comput. 40: A4184–A4207. arXiv:1705.03609. doi:10.1137/17m1135633.

[FOOTNOTECandès2016a-9] Candès, 2016a.

[FOOTNOTECandès2016b-10] Candès, 2016b.

[AbeidaZhang-11] Abeida, Habti; Zhang, Qilin; Li, Jian; Merabtine, Nadjim (2013). Iterative Sparse Asymptotic Minimum Variance Based Approaches for Array Processing. IEEE Transactions on Signal Processing (IEEE) 61 (4): 933–944. Bibcode:2013ITSP...61..933A. ISSN 1053-587X. arXiv:1802.03070. doi:10.1109/tsp.2012.2231676.

[FOOTNOTEHelgason1984Theorem_I.2.13-12] Helgason, 1984, Theorem I.2.13.

[FOOTNOTEHelgason1984Theorem_I.2.16-13] Helgason, 1984, Theorem I.2.16.

[FOOTNOTENygren1997-14] Nygren, 1997.

[15] Kiehl та Weissauer, (2001)

[FOOTNOTEvan_GinkelHendricksvan_Vliet2004-16] van Ginkel, Hendricks та van Vliet, 2004.