Плоский рух

Плоский рух можна розглядати в полярній системі координат.

Нехай ${\displaystyle \mathbf {r} }$ — це радіус-вектор з координатами ${\displaystyle (r\cos(\theta ),r\sin(\theta ))\,}$, де r і ${\displaystyle \theta }$ залежать від часу.

Використовуючи одиничні вектори

${\displaystyle {\bar {e}}_{r}=(\cos(\theta ),\sin(\theta ))\,}$

у напрямку ${\displaystyle \mathbf {r} }$, і

${\displaystyle {\bar {e}}_{\theta }=(-\sin(\theta ),\cos(\theta ))\,}$

під прямим кутом до ${\displaystyle \mathbf {r} }$, то перша і друга похідні положення будуть:

${\displaystyle {\frac {d\mathbf {r} }{dt}}={\dot {r}}{\bar {e}}_{r}+r{\dot {\theta }}{\bar {e}}_{\theta },}$

${\displaystyle {\frac {d^{2}\mathbf {r} }{dt^{2}}}=({\ddot {r}}-r{\dot {\theta }}^{2}){\bar {e}}_{r}+(r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}){\bar {e}}_{\theta }=({\ddot {r}}-r{\dot {\theta }}^{2}){\bar {e}}_{r}+{\frac {1}{r}}\quad {\dot {\overbrace {r^{2}{\dot {\theta }}} }}\quad {\bar {e}}_{\theta }}$

Похідна ${\displaystyle {\dot {r}}\,}$ задає швидкість віддалення матеріальної точки від початку координат, а похідна ${\displaystyle {\dot {\theta }}\,}$ визначає кутову швидкість.

Складова другої похідної ${\displaystyle r{\dot {\theta }}^{2}}$ називається відцентровою, а ${\displaystyle 2{\dot {r}}{\dot {\theta }}}$ — коріолісовою. Вираз для другої похідної радіус-вектора, який містить ці члени, схожий на вирази для відцентрової та коріолісової сили, що діють у системах відліку, які обретаються. Слід зауважити, що математичному виразі немає жодного фізичного змісту.[1] Фізика відцентрової та коріолісової сил проявляються у неінерційних системах відліку. Ці складові, які з'являються, коли прискорення виражається у полярних координатах, є математичним наслідком диференцюювання, тобто вони виникають у будь-якому випадку, якщо використовувати полярні координати. Так, ці складові виникають навіть якщо використовувати полярні координати в інерційних системах відліку, де ефект дії коріолісової сили ніколи не проявляється.

Коротаційна система відліку

Інерційна система відліку S та миттєва неінерційна коротаційна система відліку S' . Коротаційна система обертається з кутовою швидкістю Ω, яка дорівнює швидкості обертання частинки навколо початкового положення S' у момент часу t. Положення частинки визначаєть радіус-вектором r(t) та одиничними векторами, які зображені у радіальному напрямку до частинки відносно початкового положення та збільшення кута θ перпендикулярні до радіального напрямку. Ці одиничні вектори необов'язково повинні бути дотичними або перпендикулярними до траєкторії. Також відстань по радіусу r необов'язково пов'язана з радіусом кривизни траєкторії.

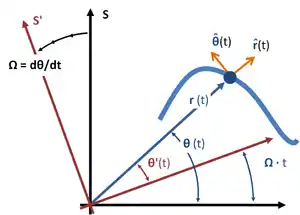
Для частинки, яка здійснює плоский рух, існує один підхід, який дає фізичне трактування відцентровій та коріолісовій складовій — це поняття коротаційної системи відліку.[2] Щоб визначити таку систему, необхідно обрати систему, у якій визначена відстань r(t) до точки. Осі обертання обираються так, щоб вони були перпендикулярними до площини руху частинки і проходили через її початок. Тоді, у деякий момент часу t швидкість обертання коротаційної системи Ω обирається такою, щоб вона збігалася зі швидкістю обертання частинки dθ/dt навколо цієї осі. Далі, члени у прискоренні в інерційній системі відліку пов'язуються з тими, що у кортаційній системі. Нехай положення частинки в інерційний системі відліку визначається координатами (r(t), θ(t)), і у коротаційній (r(t), θ'(t)). Оскільки коротаційна система обертається з такою самою швидкістю, як і частинка, то dθ'/dt = 0. Уявна відцентрова сила у коротаційній системі mrΩ² радіально спрямована назовні. Швидкість частинки у коротаційній системі також радіально спрямована назовні, оскільки dθ'/dt = 0, і має величину −2m(dr/dt)Ω, спрямована у напрямку θ. Таким чином, підставивши ці сили до запису другого закону Ньютона, отримаємо:

${\displaystyle {\boldsymbol {F}}+{\boldsymbol {F_{cf}}}+{\boldsymbol {F_{Cor}}}=m{\ddot {\boldsymbol {r}}}\ ,}$

Крапочки над символом позначають диференціювання по часу. F — це сила, яка протидіє уявним силі Коріоліса та відцентровій силі. Розклавші ці рівняння на складові отримаємо:

${\displaystyle F_{r}+mr\Omega ^{2}=m{\ddot {r}}}$

${\displaystyle F_{\theta }-2m{\dot {r}}\Omega =mr{\ddot {\theta }}\ ,}$

які можна порівняти з рівняннями в інерційній системі відліку:

${\displaystyle F_{r}=m{\ddot {r}}-mr{\dot {\theta }}^{2}\ }$

${\displaystyle F_{\theta }=mr{\ddot {\theta }}+2m{\dot {r}}{\dot {\theta }}\ .}$

Оскільки коротаційна система у момент часу t обертається зі швидкістю Ω = dθ/dt, то у поєднанні з цим порівнянням ми можемо пояснити члени у прискоренні (помножені на масу частинки), які знайдені в інерційній системі відліку, як від'ємні відцентрова та коріолісова сили. Їх можна розпізнати у миттєвій неінерційній коротаційній системі.

В загальному випадку криволінійного руху частинки (на противагу простому випадку руху по колу) відцентрова та коріолісова сили у пов'язаній з частинкою системі відліку відносяться до уявного кола, до якого дотична швидкість частинки в певний момент часу. Центр цього кола не обов'язково збігається з початком координат.

• Яворський Б. М., Детлаф А. А., Лебедев А. К. Довідник з фізики для інженерів та студентів вищих навчальних закладів / Переклад з 8-го переробл. і випр. вид. — Т. : Навчальна книга — Богдан, 2007. — 1040 с. — ISBN 966-692-818-3.
• Сивухин Д. В. Общий курс физики. — Издание 5-е, стереотипное. — М.: Физматлит, 2006. — Т. I. Механика. — 560 с.