Поляризаційна тотожність
У лінійній алгебрі поляризаційна тотожність виражає скалярний добуток двох векторів через норму у нормованому векторному просторі. Поляризаційна тотожність зокрема описує коли норма породжується деяким скалярним добутком.
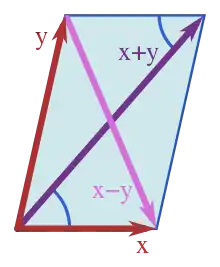
Поляризаційна тотожність тісно пов'язана із правилом паралелограма, адже для нормованого простору (V, ), скалярний добуток на V для якого існує якщо і тільки якщо виконується правило паралелограма. Тоді скалярний добуток однозначно виражається через норму саме за допомогою поляризаційних тотожностей:[1][2].
Формули
Будь-який скалярний добуток на векторному просторі породжує норму:
Поляризаційні тотожності навпаки виражають скалярний добуток через норму (у випадках коли норма породжена скалярним добутком).
Дійсні векторні простори
Якщо векторний простір є над полем дійсних чисел, тоді виконують рівності:
Різні варіанти поляризаційних тотожностей є еквівалентними згідно правила паралелограма:
Формули виводяться із властивостей скалярного добутку:
і аналогічно
Виразивши скалярний добуток через норми у цих тотожностях можна одержати перші дві форми поляризаційної тотожності. Віднявши від першої рівності другу можна одержати третю форму.
Комплексні векторні простори
Дійсна частина скалярного добутку (незалежно від того чи він є у дійсних чи комплексних просторах і антилінійним по першій чи другій координаті) є симетричною білінійною формою, яку можна виразити поляризаційною тотожністю:
Натомість уявна частина залежить від того чи добуток є антилінійним по першій чи другій координаті.
Якщо скалярний добуток є антилінійним по першій координаті, тоді для всіх
- .
Якщо скалярний добуток є антилінійним по другій координаті, тоді для всіх
Останню рівність також можна записати як::
Знаходження скалярного добутку у нормованому просторі
Якщо у нормованому просторі (V, ) виконується правило паралелограма
тоді поляризаційні тотожності задають скалярний добуток для якого для всіх .
Це означає, що, наприклад, для дійсних векторних просторів, якщо виконується правило паралелограма, то функція, значення якої для є рівним є скалярним добутком.
Доведення
Доведення дано для дійсних нормованих просторів. Для комплексних доведення аналогічне.
Якщо норма задана скалярним добутком, то вона задовольняє поляризаційну тотожність
- для всіх
Нехай тепер маємо довільний дійсний нормований простір із нормою , що задовольняє правило паралелограма. Тоді введена вище функція є скалярним добутком, що породжує норму, тобто:
- для всіх
- для всіх і всіх
(властивості і тоді випливають із аналогічних властивостей норми).
Властивості (1) і (2) відразу випливають із підстановки: і властивості: .
Для доведення (3) необхідно довести:
Еквівалентно:
До доданків у лівій стороні можна застосувати правило паралелограма:
Тоді після підстановки і перетворень одержується:
Але остання рівність одержується як різниця двох рівностей із правила паралелограма:
Це завершує доведення властивості (3).
Із властивості (3) випливає для і тоді елементарно для всіх Але із виконання (4) для випливає (4) для . Але скалярний добуток, сума і норма є неперервними у нормованому просторі, тому одержана внаслідок поляризаційної тотожності функція є неперервною від дійснозначного аргумента . Тому оскільки ця функція є рівною 0 для раціональних чисел, вона має бути рівною 0 і для всіх дійсних чисел, що завершує доведення властивості (4).
Узагальнення
Симетричні білінійні форми
Якщо B є симетричною білінійною формою на векторному просторі, і Q є квадратичною формою заданою як
то
Цю формулу можна застосувати навіть у випадку полів характеристика яких є рівною 2, хоча у цьому випадку ліва сторона в усіх формулах буде рівною 0. У цьому випадку не існує формули для симетричних білінійних форм через квадратичні форми і ці два поняття є нееквівалентними.
Формули також можна застосувати для білінійних форм на модулях над комутативними кільцями, хоча знову ж квадратичну форму можна виразити через симетричну лише якщо 2 є оборотним елементом у кільці, в іншому випадку поняття не є еквівалентними. Наприклад для цілих чисел існують квадратичні форми і симетричні форми.
Примітки
- Philippe Blanchard, Erwin Brüning (2003). Proposition 14.1.2 (Fréchet–von Neumann–Jordan). Mathematical methods in physics: distributions, Hilbert space operators, і variational methods. Birkhäuser. с. 192. ISBN 0817642285.
- Gerald Teschl (2009). Theorem 0.19 (Jordan–von Neumann). Mathematical methods in quantum mechanics: with applications to Schrödinger operators. American Mathematical Society Bookstore. с. 19. ISBN 978-0-8218-4660-5.
- Butler, Jon (20 червня 2013). norm - Derivation polarization identities?. Mathematics Stack Exchange. Архів оригіналу за 14 жовтня 2020. Процитовано 14 жовтня 2020. See Harald Hanche-Olson's answer.
