Правила де Моргана
Правила де Моргана — властивість булевих алгебр, що дозволяє виразити одну з двоїстих операцій через іншу і унарну операцію доповнення (заперечення). Особливо часто використовуються у алгебрі множин і алгебрі логіки, що є прикладами булевої алгебри. Названі на честь британського математика і логіка Ауґустуса де Моргана.
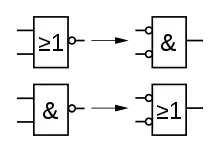
Твердження
Для булевої алгебри
Нехай є деяка булева алгебра, тоді для справджується:
Мають місце також узагальнені правила де Моргана:
- ,
- .
Для алгебри логіки
| Правила перетворення |
|---|
| Числення висловлень |
| Правила висновування |
|
| Правила підстановки |
|
| Предикатна логіка |
|
Універсальне узагальнення / конкретизація |
Перше правило де Моргана:
- ,
Друге правило де Моргана
- ;
В обох цих формулах — логічна диз'юнкція, — логічна кон'юнкція, — логічне заперечення (негація), p, q — деякі логічні висловлення.
Істинність даних правил можна підтвердити за допомогою таблиць істинності
0 0 0 1 1 1 1 0 1 0 1 1 0 1 1 0 0 1 0 1 1 1 1 1 0 0 0 0
0 0 0 1 1 1 1 0 1 1 0 1 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0
Для алгебри множин
Нехай — деяка множина і — її підмножини. Тоді виконується:
- ,
де — стандартні позначення для об'єднання множин, перетину та доповнення множин.
Також виконуються і узагальнені правила
- ,
- ,
де
Доведення в теорії
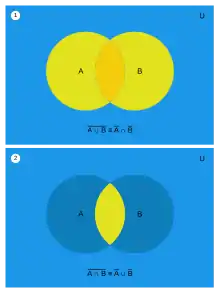
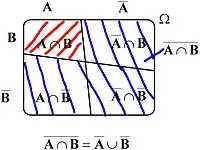
Правила засновані на відношеннях
- ,
які графічно представлені ілюстраціями нижче. Дано дві множини A і В, які є підмножинами Ω (універсуму). Діаграма 1 показує їх розташування відносно одна до одної. У діаграмі 2 показано, як формується . У діаграмі 3 на прикладі можна побачити що обидві множини рівні.
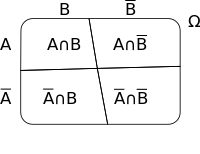 |
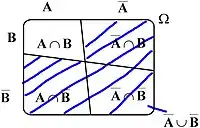 |
 |
| Розподіл простору в А та В |
Історія
Правила де Моргана були названі на честь британського математика Ауґустуса де Моргана (1806—1871), який застосував формальну версію правил до класичної логіки висловлювань. Формуляція де Моргана створена на основі логіки, започаткованої Джорджем Булем. Схожі спостереження були зроблені Арістотелем, відомим грецьким логіком. Закони де Моргана можуть бути підтверджені просто і навіть здатися тривіальними. Тим не менше, ці закони є корисними в створенні значимих висновків в доказах і результатах дедуктивного міркування.
Див. також
Посилання
- Правила де Моргана на сайті MathWorld(англ.)
- Правила де Моргана на сайті PlanetMath(англ.)