Алгебра логіки

В той час як в елементарній алгебрі вирази як правило виражаються в числах, в алгебрі логіки вони виражають значення істинності істина і хибність. Ці значення задають за допомогою біт (або двійкових чисел), а саме 0 та 1. Вони не поводять себе так само як цілі числа 0 та 1, для яких 1 + 1 = 2, а можуть визначатися як елементи дво-елементного поля GF(2), що є, цілочисловою арифметикою за модулем 2, для якої 1 + 1 = 0. Алгебра логіки також вивчає функції, що приймають значення в множині {0, 1}.

Спочатку проблематика алгебри логіки перетиналась з проблематикою алгебри множин (теоретико-множинні операції).

Проте із закінченням формування теорії множин (70-і роки 19 ст.), яка включила в себе алгебру множин, і подальшим розвитком математичної логіки, предмет алгебри логіки значно змінився.

Сучасна алгебра логіки розглядає операції над висловлюваннями (див. Числення висловлень) як булеву функцію і вивчає відносно них такі питання, як:

• таблиці істинності;
• функціональна повнота;
• замкнені класи;
• представлення у вигляді: ДНФ, КНФ, полінома Жегалкіна.

Як уже зазначалося, базовими операціями булевої алгебри (алгебри логіки) є наступні логічні операції:

• І (кон'юнкція), позначається x∧y (іноді x І y), задовольняє x∧y = 1, якщо x = y = 1 та x∧y = 0 в інших випадках.
• АБО (диз'юнкція), позначається x∨y (іноді x АБО y), задовольняє x∨y = 0, якщо x = y = 0 та x∨y = 1 в інших випадках.
• НІ (заперечення), позначається ¬x (іноді НЕ x або !x), задовольняє ¬x = 0, якщо x = 1 та ¬x = 1, якщо x = 0.

Альтернативним способом значення x∧y, x∨y, та ¬x можна представити у табличному вигляді для всіх можливих значень за допомогою таблиць істинності наступним чином.

${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x\wedge y}$ ${\displaystyle x\vee y}$ 0 0 0 0 1 0 0 1 0 1 0 1 1 1 1 1

${\displaystyle x}$ ${\displaystyle \neg x}$ 0 1 1 0

Якщо значення істинності 0 та 1 інтерпретувати як цілі числа, ці операції можна було задати як звичайні операції арифметики (де x + y використовує додавання а xy використовує множення), або як функції мінімуму/максимуму:

${\displaystyle {\begin{aligned}x\wedge y&=xy=\min(x,y)\\x\vee y&=x+y-xy=\max(x,y)\\\neg x&=1-x\end{aligned}}}$

Можна вважати, що лише заперечення і одна із двох операцій, що залишилися, є базовими, оскільки наступні рівняння дозволяють визначити кон'юнкцію через операції заперечення та диз'юнкцію, і навпаки:

${\displaystyle {\begin{aligned}x\wedge y&=\neg (\neg x\vee \neg y)\\x\vee y&=\neg (\neg x\wedge \neg y)\end{aligned}}}$

Три булеві операції описані вище називають базовими або первинними, що означає, що вони можуть бути базисом для всіх інших булевих операцій, оскільки всі інші операції можна виразити через них за допомогою композиції. Серед операцій, які можна побудувати із базових операцій є наступні:

${\displaystyle x\rightarrow y=\neg {x}\vee y}$

${\displaystyle x\oplus y=(x\vee y)\wedge \neg {(x\wedge y)}=(x\wedge \neg y)\vee (\neg x\wedge y)}$

${\displaystyle x\equiv y=\neg {(x\oplus y)}=(x\wedge y)\vee (\neg x\wedge \neg y)}$

Ці визначення дають наступні таблиці істинності, в яких показані значення цих операцій для всіх можливих вхідних значень.

${\displaystyle x}$	${\displaystyle y}$	${\displaystyle x\rightarrow y}$	${\displaystyle x\oplus y}$	${\displaystyle x\equiv y}$
0	0	1	0	1
1	0	0	1	0
0	1	1	1	0
1	1	1	0	1

Перша операція, x → y, називається імплікацією. Якщо x є істинним, тоді за значення виразу x → y приймається значення y. Але якщо x приймає хибне значення, то значення y можна було б ігнорувати; однак ця операція повинна повернути деяке логічне значення, і існує лише два варіанти вибору. То ж за визначенням, x → y є істиною коли x є хибним.

Друга операція, x ⊕ y, називається виключною диз'юнкцією (часто задається як абревіатура XOR), аби відрізнити її від диз'юнкції. Вона є істиною, лише коли x та y різні.

Третя операція, обернена до виключної диз'юнкції, називається еквівалентність або булева рівність: x ≡ y буде істиною, лише коли x та y мають однакове значення.

Для двох даних операндів, кожен з яких має 2² = 4 можливих комбінації входів. Оскільки кожен вихід може мати два можливих значення, існує загалом 2⁴ = 16 можливих булевих операцій.

Булева алгебра задовольняє багатьом відповідним законам звичайної алгебри, якщо якщо співставити операції ∨ із додаванням, а ∧ із множенням. Зокрема наступні закони є спільними для обох типів алгебр:[6]

Асоціативність операції ${\displaystyle \vee }$:		${\displaystyle x\vee (y\vee z)}$	${\displaystyle =(x\vee y)\vee z}$
Асоціативність операції ${\displaystyle \wedge }$:		${\displaystyle x\wedge (y\wedge z)}$	${\displaystyle =(x\wedge y)\wedge z}$
Комутативність операції ${\displaystyle \vee }$:		${\displaystyle x\vee y}$	${\displaystyle =y\vee x}$
Комутативність операції ${\displaystyle \wedge }$:		${\displaystyle x\wedge y}$	${\displaystyle =y\wedge x}$
Дистрибутивність операції ${\displaystyle \wedge }$ over ${\displaystyle \vee }$:		${\displaystyle x\wedge (y\vee z)}$	${\displaystyle =(x\wedge y)\vee (x\wedge z)}$
Ідентичність для ${\displaystyle \vee }$:		${\displaystyle x\vee 0}$	${\displaystyle =x}$
Ідентичність для ${\displaystyle \wedge }$:		${\displaystyle x\wedge 1}$	${\displaystyle =x}$
Анігілятор для ${\displaystyle \wedge }$:		${\displaystyle x\wedge 0}$	${\displaystyle =0}$

Наступні закони є дійсними в булевій алгебрі, але не дійсні в звичайній алгебрі:

Анігілятор для ${\displaystyle \vee }$:		${\displaystyle x\vee 1}$	${\displaystyle =1}$
Ідемпотентність ${\displaystyle \vee }$:		${\displaystyle x\vee x}$	${\displaystyle =x}$
Ідемпотентність ${\displaystyle \wedge }$:		${\displaystyle x\wedge x}$	${\displaystyle =x}$
Абсорбція 1:		${\displaystyle x\wedge (x\vee y)}$	${\displaystyle =x}$
Абсорбція 2:		${\displaystyle x\vee (x\wedge y)}$	${\displaystyle =x}$
Дистрибутивність операції ${\displaystyle \vee }$ над ${\displaystyle \wedge }$:		${\displaystyle x\vee (y\wedge z)}$	${\displaystyle =(x\vee y)\wedge (x\vee z)}$

Якщо прийняти x = 2 в третьому наведеному вище законі, ми бачимо що це не закон із звичайної алгебри, оскільки 2×2 = 4. Решта п'ять законів можна фальсифікувати у звичайні алгебрі, якщо прийняти що значення усіх змінних буде 1, наприклад, в законі абсорбції 1 ліва сторона відношення була б 1(1+1) = 2, а права частина рівняння була 1, і так далі.

Всі ці закони, що розглядалися досі, були для кон'юнкції та диз'юнкції. Ці дві операції мають властивість, що при зміні будь-якого з аргументів, вихід залишиться або незмінним, або змінить своє значення так само як вхід. Аналогічно, зміна значення будь-якої змінною з 0 на 1 ніколи не призведе до того, що вихід змінить своє значення з 1 на 0. Операції з такою властивістю називають монотонними. Таким чином всі аксіоми досі були для монотонної булевої логіки. Немонотонність з'являється через операцію доповнення ¬, що наведено далі.[5]

Операція доповнення (заперечення) визначається наступними двома законами.

${\displaystyle {\begin{aligned}&{\text{Доповнення 1}}&x\wedge \neg x&=0\\&{\text{Доповнення 2}}&x\vee \neg x&=1\end{aligned}}}$

Всі властивості заперечення, включаючи закони що наведені нижче, випливають із двох вищенаведених законів.[5]

Як у звичайній так і у булевій алгебрі, операція заперечення працює як обмін пари елементів, тому в обох алгебрах вона задовольняє закону подвійного заперечення (також називається законом інволюції)

${\displaystyle {\begin{aligned}&{\text{Подвійне заперечення}}&\neg {(\neg {x})}&=x\end{aligned}}}$

Але тоді як «звичайна алгебра» задовольняє наступним двом законам

${\displaystyle {\begin{aligned}(-x)(-y)&=xy\\(-x)+(-y)&=-(x+y)\end{aligned}}}$

Булева алгебра задовольняє Законам де Моргана:

${\displaystyle {\begin{aligned}&{\text{де Моргана 1}}&\neg x\wedge \neg y&=\neg {(x\vee y)}\\&{\text{де Моргана 2}}&\neg x\vee \neg y&=\neg {(x\wedge y)}\end{aligned}}}$

Закони описані вище визначають булеву алгебру, в тому сенсі що з них випливають усі інші наслідки. Для цього достатньо законів доповнення 1 та 2, разом із законами монотонності. Таким чином їх можна вважати повною множиною законів або однією із можливих систем аксоіматизації булевої алгебри. Кожен закон булевою алгебри випливає логічним чином із цих аксіом. Крім того, булеві алгебри можна визначити як моделі із цих аксіом.

Принцип: Якщо {X, R} — частково впорядкована множина, тоді {X, R(обернена)} також частково впорядкована множина.

Ніякої магії у виборі символів для позначення логічних значень булевої алгебри не існує. Замість 0 і 1 можна було б використовувати, наприклад, α та β, доки ми робимо це послідовним чином повсюди, це досі залишатиметься булевою алгеброю, але із явними зовнішніми відмінностями.

Припустимо також, що ми переназвали 0 та 1 відповідно на 1 та 0. Тоді це також залишатиметься булевою алгеброю, що навіть оперує з тими ж значеннями. Однак вона не буде ідентичною до нашої початкової булевої алгебри, оскільки тепер операція ∨ буде поводити так, як поводила себе операція ∧ і навпаки. Тож, вони також матимуть зовнішні відмінності, які показують що ми змінили позначення, не дивлячись на те, що ми досі використовуємо 0-і та 1-і.

Але якщо в додаток до того, що ми замінили місцями імена змінних, ми замінимо місцями імена двох двійкових операцій, тепер немає ніякого сліду від того що ми зробили. Кінцевий результат повністю не відрізняється від того, з чого ми почали. Ми помітимо, що колонки для операцій x∧y та x∨y в таблицях істинності змінили свої місця, але ця відмінність є незначною.

Коли існує така пара операцій, для яких все залишається незмінним, якщо всі пари були одночасно взаємно змінені, ми називаємо такі елементи кожної пари двоїстими один з одним. Таким чином 0 та 1 є двоїстими, а також операції ∧ та ∨ є двоїстими. Принцип двоїстості, також називають двоїстістю де Моргана, за якою стверджують, що булева алгебра залишається незмінною, якщо взаємно замінити всі двоїсті пари.

Діаграма Венна[7] — це графічне представлення булевих операцій за допомогою зафарбованих областей, що перекриваються. По одній області для кожної змінної, всі області круглі як показано на прикладах. Внутрішня і зовнішня частина області x відповідає відповідно значенням 1 (істина) та 0 (хибність) для змінної x. Зафарбована область показує значення операції для кожної комбінації цих областей, де зафарбована область означає 1, а не зафарбована — 0 (але в деяких книжках може зустрітися і навпаки).

Діаграми Венна на малюнку знизу показують операції кон'юнкції x∧y, диз'юнкції x∨y, та доповнення ¬x.

Діаграми Венна для кон'юнкції, диз'юнкції та доповнення

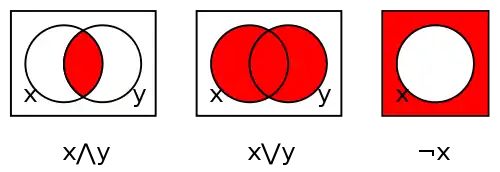
Для кон'юнкції, регіон в середині двох кругів зафарбований, що означає що вираз x∧y дорівнює 1, коли обидві змінні мають значення 1. Інші області лишилися не зафарбованими, аби зазначити, що x∧y дорівнює 0 для всіх інших комбінацій.

На другій діаграмі, що показує диз'юнкцію x∨y зафарбована область, що знаходиться в середині двох кіл одночасно. Третя діаграма представляє доповнення ¬x, де зафарбована область не в середині кола.

Тут не показані діаграми для сталих 0 та 1, оскільки вони тривіальні, і представляються незафарбованим або зафарбованим прямокутником, без кіл в середині. Однак ми б могли розмістити коло для змінної x в цих прямокутниках, в такому випадку це б позначало функцію із одним аргументом, x, що позначає те саме значення, незалежно від x, що називається константною функцією. Що стосується результатів функцій, то константи і константні функції не відрізняються; їх відмінність полягає в тому, що константа не приймає ніяких аргументів, і називається нульовою операцією, в той час як константна функція приймає один аргумент, який ігнорується, і тому є унарною операцією.

Діаграми Венна є корисними для візуалізації законів. Закони комутативності для ∧ та ∨ можна побачити із симетричності діаграм: бінарна операція, що не є комутативною не мала б симетричної діаграми, оскільки заміна місцями x та y призвело до горизонтального віддзеркалення діаграми, і відсутність комутативності б відзначилася у не симетричності діаграми.

Ідемпотентність операцій ∧ та ∨ можна було б зобразити зсунувши два кола разом і зазначивши, що зафарбована область тоді стає цілим колом, як обох ∧ та ∨.

Цифрова логіка застосовує булеву алгебру для 0 та 1 до електронної апаратури, що складається із логічних елементів з'єднаних між собою, і які утворюють електричну схему. Кожний елемент виконує булеву операцію, і в різних системах позначень позначається таким чином, що його вигляд ідентифікує певну операцію. Форми позначень для елементів, що позначають кон'юнкцію (І-вентиль), диз'юнкцію (АБО-вентиль), і доповнення (інвертори) виглядають наступним чином.[8]

Лінії по лівій стороні кожного елементу позначають вхідні з'єднання або порти. Значення на вході задається напругою. Для так званої логіки з «активним високим рівнем», 0 задається значенням напруги близьким до нуля або «землі», в той час як 1 задається значенням напруги близьким до джерела напруги; при активному низькому рівні все буде навпаки. Лінія по правій стороні від кожного елемента задає вихідний порт, який як правило має ті самі узгодження щодо напруги, що і вхідні порти.

Доповнення виконується інвертуючим вентилем. Трикутник позначає операцію, яка просто копіює вхід на вихід; невелике коло на виході позначає фактичну дію доповнення до входу. У даній системі позначень розташування кола біля будь-якого порту означає, що сигнал проходячи через цей порт буде інвертований пройшовши крізь нього, не залежно від того це вхідний чи вихідний порт.

Принцип двоїстості, або Правила де Моргана, можна розуміти як твердження: що доповнення всіх трьох портів І вентиля перетворює його на вентиль АБО і навпаки, як показано на малюнку нижче. Доповнення обох портів інвертора залишає операцію незмінною.

На початку 20-го століття, декілька електротехніків інтуїтивним способом зрозуміли, що булева алгебра аналогічна поведінці певних електричних схем. Клод Шеннон формально довів що така поведінка логічно еквівалентна булевій алгебрі в 1937 році.

Сьогодні, всі сучасні комп'ютери загального призначення виконують свої функції за допомогою булевої логіки двох значень; таким чином, їх електричні кола є фізичним втіленням булевої алгебри для двох значень. Вони досягають це багатьма способами: за допомогою напруги на з'єднаннях в високочастотних схемах і ємнісних пристроях зберігання даних, за допомогою орієнтації магнітного поля в феромагнітних пристроях зберігання інформації, за допомогою перфорації в перфокартах або паперових стрічках, і так далі. (деякі перші комп'ютери використовували десяткові кола або механізми замість двозначної логіки в електричних колах.)

Звісно, можна закодувати більше ніж два символа. Наприклад, можна використати відповідні значення в 0, 1, 2, і 3 вольта аби закодувати алфавіт з чотирьох символів, або робити отвори різного розміру в перфокартах. На практиці, обмеження по швидкодії, малими розмірами, низьким енергоспоживанням об'єднуються так, що вирішальним фактором стають шуми. І стає важче відрізняти символи, коли в одному місці можуть виникнути декілька можливих символів. Замість того, щоб намагатися розрізнити чотири різні напруги на дроті, інженери цифрових схем зупинилися на двох значеннях напруги, високе і низьке.

Комп'ютери використовують булеві схеми для двох значень з описаних вище причин. Самі типові архітектури комп'ютерів використовують впорядковані послідовності булевих значень, наприклад, в 32 або 64 значень, які називають бітами. 01101000110101100101010101001011. При програмуванні на машинному коді, мові асемблера, і певних інших мовах програмування, програмісти працюють із низькорівневою цифровою структурою із регістрів даних. Ці регістри працюють із рівнями напруги, при яких близьке до нуля значення напруги представляє булеве значення 0, і опорна напруга (часто +5V, +3.3V, +1.8V) задає булеве значення 1. Такі мови підтримують числові операції і логічні операції. В контексті, «числові» означає, що комп'ютер розглядатиме послідовність бітів як двійкові числа (числа із основою два) і виконуватиме арифметичні операції такі як додавання, віднімання, множення або ділення. «Логічні» відноситься до логічних булевих операцій диз'юнкції, кон'юнкції і заперечення між двома послідовностями біт, при яких кожен біт однієї послідовності простим способом порівнюється з відповідним бітом в іншій послідовності. Таким чином програмісти мають можливість обирати як працювати, застосовуючи правила числової алгебри чи булевої алгебри в залежності від потреби. Основною відмінною функцією між родинами операцій є існування операції переносу у першій алгебрі, і відсутність у останній.