Ряд Меркатора

Площа під гіперболою ${\displaystyle y=1/x}$ в інтервалі ${\displaystyle (1,a)}$ дорівнює ${\displaystyle \ln(a)}$

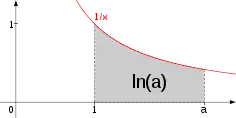
У 1647 Грегуар де Сен-Венсан виявив зв'язок логарифма і площі під гіперболою (див. рисунок). У 1650 році, виходячи з геометричних міркувань, італійський математик П'єтро Менголі опублікував у своєму трактаті «Нові арифметичні квадратури» розкладання ${\displaystyle \ln 2}$ в нескінченний ряд:[1]

${\displaystyle \ln 2={\frac {1}{1\cdot 2}}+{\frac {1}{3\cdot 4}}+{\frac {1}{5\cdot 6}}+\cdots .}$

У 1657 році цю формулу незалежно опублікував англійський математик Вільям Браункер в своїй статті «Квадратура гіперболи за допомогою нескінченного ряду раціональних чисел».[1]

У 1668 році німецький математик Ніколас Меркатор (Кауфман), який проживав тоді в Лондоні, в трактаті «Logarithmotechnia» вперше розглянув розкладання в ряд не числа, а функції:[2]

${\displaystyle {\frac {1}{1+x}}=1-x+x^{2}-x^{3}+\dots }$

Далі він знайшов площі під лівою і правою частинами цього розкладу (в сучасних термінах, проінтегрував їх) і отримав «ряд Меркатора», який виписав для значень ${\displaystyle x=0{,}1}$ та ${\displaystyle x=0{,}21}$. Збіжність ряду Меркатор не дослідив, але відразу після виходу в світ праці Меркатора Джон Валліс вказав, що ряд придатний при ${\displaystyle 0\leqslant x<1}$ (від'ємними числами тоді нехтували).

Як виявили історики, Ньютон вивів такий же ряд в 1665 році, але, за своїм звичаєм, не подбав про публікацію[2]. Глибокі дослідження Ньютона в області нескінченних рядів були опубліковані тільки в 1711 році, в трактаті «Аналіз за допомогою рівнянь з нескінченним числом членів».[3]

Ряд можна отримати з теореми Тейлора методом індукції через обчислення ${\displaystyle n}$-ї похідної функції ${\displaystyle \ln(x)}$ у точці ${\displaystyle x=1}$, починаючи з

${\displaystyle {\frac {d}{dx}}\ln(x)={\frac {1}{x}}.}$

Також можна почати з скінченного геометричного ряду (${\displaystyle t\neq -1}$):

${\displaystyle 1-t+t^{2}-\cdots +(-t)^{n-1}={\frac {1-(-t)^{n}}{1+t}}}$

з якого отримуємо

${\displaystyle {\frac {1}{1+t}}=1-t+t^{2}-\cdots +(-t)^{n-1}+{\frac {(-t)^{n}}{1+t}}.}$

З цього випливає, що

${\displaystyle \int _{0}^{x}{\frac {{\rm {d}}t}{1+t}}=\int _{0}^{x}\left(1-t+t^{2}-\cdots +(-t)^{n-1}+{\frac {(-t)^{n}}{1+t}}\right)\ {\rm {d}}t}$

і шляхом почленного інтегрування маємо

${\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots +(-1)^{n-1}{\frac {x^{n}}{n}}+(-1)^{n}\int _{0}^{x}{\frac {t^{n}}{1+t}}\ {\rm {d}}t.}$

Якщо ${\displaystyle -1<x\leq 1}$, залишковий член прямує до 0 при ${\displaystyle n\to \infty }$.

Якщо цей вираз проінтегрувати ${\displaystyle k}$ разів, то отримаємо

${\displaystyle -xA_{k}(x)+B_{k}(x)\ln(1+x)=\sum _{n=1}^{\infty }(-1)^{n-1}{\frac {x^{n+k}}{n(n+1)\cdots (n+k)}},}$

де

${\displaystyle A_{k}(x)={\frac {1}{k!}}\sum _{m=0}^{k}{k \choose m}x^{m}\sum _{l=1}^{k-m}{\frac {(-x)^{l-1}}{l}}}$

та

${\displaystyle B_{k}(x)={\frac {1}{k!}}(1+x)^{k}}$

є многочленами змінної ${\displaystyle x}$.[4]

Якщо у ряді Меркатора покласти ${\displaystyle x=1}$, то отримуємо знакозмінний гармонійний ряд

${\displaystyle \sum _{k=1}^{\infty }{\frac {(-1)^{k+1}}{k}}=\ln(2).}$

Ряд Меркатора непридатний для реальних розрахунків, так як збігається дуже повільно, причому в обмеженому інтервалі. Але вже в рік публікації роботи Меркатора (1668) Джеймс Грегорі запропонував його модифікований варіант:

${\displaystyle \ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \right).}$

Цей ряд збігається набагато швидше, а логарифмований вираз вже може бути будь-яким додатним числом [5]. Наприклад, сума перших 10 членів ряду Меркатора для ${\displaystyle \ln 2}$ дорівнює ${\displaystyle 0{,}646}$, тут тільки перший десятковий знак вірний, в той час як ряд Грегорі дає значення ${\displaystyle 0{,}6931471805498}$, в якому вірні 10 знаків з 13.[6].

На комплексній площині ряд Меркатора набуває узагальнений вигляд:

${\displaystyle \sum _{n=1}^{\infty }{\frac {z^{n}}{n}}=z+{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}+{\frac {z^{4}}{4}}+\cdots .}$

Це ряд Тейлора для комплексної функції ${\displaystyle f(z)=-\ln(1-z)}$, де символ ${\displaystyle \ln }$ позначає головну вітку (головне значення) комплексного натурального логарифма. Даний ряд збігається в крузі ${\displaystyle |z|\leqslant 1,z\neq 1}$.

Насправді, як видно з ознаки д'Аламбера, ряд має радіус збіжності рівний 1, тому збігається абсолютно у кожному крузі ${\displaystyle B(0,r)}$ з радіусом ${\displaystyle r<1}$. Більше того, він рівномірно збігається на кожному виколотому крузі ${\displaystyle {\overline {B(0,1)}}\setminus B(1,\delta )}$ з ${\displaystyle \delta >0}$. Це відразу випливає з алгебраїчної тотожності:

${\displaystyle (1-z)\sum _{n=1}^{m}{\frac {z^{n}}{n}}=z-\sum _{n=2}^{m}{\frac {z^{n}}{n(n-1)}}-{\frac {z^{m+1}}{m}},}$

оскільки ряд у правій частині рівномірно збігається на всьому замкненому одиничному крузі.

• Ряд Тейлора
• Гармонічний ряд
• Геометричний ряд

• Weisstein, Eric W. Mercator Series(англ.) на сайті Wolfram MathWorld.
• Eriksson, Larsson & Wahde. Matematisk analys med tillämpningar, part 3. Gothenburg 2002. p. 10.
• Some Contemporaries of Descartes, Fermat, Pascal and Huygens from A Short Account of the History of Mathematics (4th edition, 1908) by W. W. Rouse Ball.