Снарк Блануші
Снарк Блануші — 3-регулярний граф з 18 вершинами і 27 ребрами[2]. Існують два таких графи. Обидва ці графи знайшов у 1946 році югославський математик Данило Блануші, на честь якого вони й названі[3]. На той час був відомий лише один снарк — граф Петерсена.
| Снарк Блануші | |
|---|---|
 Перший снарк Блануші | |
| Названий на честь | Данило Блануші |
| Вершин | 18 |
| Ребер | 27 |
| Діаметр | 4 |
| Обхват | 5 |
| Автоморфізм |
8, D4(1-й) 4, группа Клейна (2-й) |
| Хроматичне число | 3 |
| Хроматичний індекс | 4 |
| Властивості |
Снарк гіпогамільтонів кубічний тороїдальний.[1] |
Як і всі снарки, снарки Блануші є зв'язними кубічними графами без мостів з хроматичним індексом 4. Обидва мають хроматичне число 3, діаметр 4 і обхват 5. Вони негамільтонові, але гіпогамільтонові[4].
Алгебраїчні властивості
Група автоморфізмів першого Снарка Блануші має порядок 8 і ізоморфна діедральній групі — групі симетрії квадрата.
Група автоморфізмів другого Снарка Блануші є абелевою групою близько 4 і ізоморфна 4-групі Клейна — прямим твором циклічної групи на себе.
Характеристичні многочлени першого і другого снарка Блануші:
- ,
- .
Узагальнені снарки Блануші
Існують узагальнення першого і другого снарка Блануші до двох нескінченних родин снарка порядку , які позначаються и . Снарк Блануші є найменшими членами цих двох сімейств[5].
У 2007 Мазак (J. Mazak) довів, що циклової хроматичний індекс узагальнених снарка Блануші дорівнює [6].
У 2008 Геблех (M. Ghebleh) довів, що циклової хроматичний індекс узагальнених снарка Блануші дорівнює [7].
Галерея
 Хроматичне число першого снарка Блануші дорівнює 3.
Хроматичне число першого снарка Блануші дорівнює 3. Хроматичний індекс першого снарка Блануші дорівнює 4.
Хроматичний індекс першого снарка Блануші дорівнює 4. Хроматичний індекс другого снарка Блануші дорівнює 3.
Хроматичний індекс другого снарка Блануші дорівнює 3.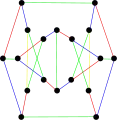 Хроматичний індекс другого снарка Блануші дорівнює 4.
Хроматичний індекс другого снарка Блануші дорівнює 4.
Примітки
- Orbanić, Alen; Pisanski, Tomaž; Randić, Milan; Servatius, Brigitte (2004). Blanuša double. Math. Commun. 9 (1): 91–103.
- Weisstein, Eric W. Blanuša snarks(англ.) на сайті Wolfram MathWorld.
- Данило Блануша, «Problem cetiriju boja.» Glasnik Mat. Fiz. Astr. Ser. II. 1, 31-42, 1946.
- Eckhard Steen, «On Bicritical Snarks» Math. Slovaca, 1997.
- Read, R. C. and Wilson, R. J. An Atlas of Graphs. Oxford, England: Oxford University Press, pp. 276 and 280, 1998.
- J. Mazak, Circular chromatic index of snarks, Master's thesis, Comenius University in Bratislava, 2007.
- M. Ghebleh, Circular Chromatic Index of Generalized Blanuša Snarks, The Electronic Journal of Combinatorics, vol 15, 2008.