Графічний конвеєр
У комп'ютерній графіці графічний конвеєр або конвеєр рендерингу — це концептуальна модель, яка описує, які кроки потрібно виконати графічній системі для рендерингу тривимірної сцени на двовимірний екран. Після створення 3D–моделі, наприклад, у відеогрі чи будь-якій іншій 3D-комп'ютерній анімації, графічний конвеєр — це процес перетворення цієї 3D–моделі в те, що зображається на комп'ютері. Оскільки кроки, необхідні для цієї операції, залежать від використовуваного програмного та апаратного забезпечення та бажаних характеристик дисплея, не існує універсального графічного конвеєра, який підходить для всіх випадків. Однак інтерфейси програмування графічних прикладних програм (API), такі як Direct3D і OpenGL, були створені для уніфікації подібних кроків та управління графічним конвеєром певного апаратного прискорювача. Ці інтерфейси API абстрагуються від базового обладнання та дозволяють програмісту уникати написання коду для управління прискорювачами графічного обладнання (AMD/Intel/NVIDIA, тощо).
Модель графічного конвеєра зазвичай використовується при візуалізації в режимі реального часу. Найчастіше більшість етапів конвеєра реалізовані апаратно, що дозволяє проводити спеціальні оптимізації. Термін «конвеєр» використовується в аналогічному сенсі до конвеєра в процесорах: окремі етапи конвеєру виконуються паралельно, але блокуються до тих пір, поки не буде виконаний найповільніший крок.
Концепція
3D конвеєр зазвичай відноситься до найпоширенішої форми комп'ютерного 3D–рендерингу, яка називається 3D полігональне моделювання відмінна від трасування променів та кидання променів. При киданні променів виникає в точці, де знаходиться камера, і якщо цей промінь потрапляє на поверхню, розраховується колір і освітлення точки на поверхні, де обчислюється удар. У режимі рендерингу багатокутника в 3D відбувається зворотне – обчислюється площа, яка переглядається камерою, а потім створюються промені від кожної частини кожної поверхні з огляду на камеру і відслідковуються до камери.[1]
Структура
Графічний конвеєр можна розділити на три основні частини: Застосування, Геометрія та Растеризація.[2]

Програма
Крок програми виконується програмним забезпеченням на головному процесорі (CPU). На кроці програми внесення змін до сцени за потреби, наприклад, шляхом взаємодії користувача за допомогою пристрою введення або під час анімації.У сучасному ігровому рушії, такому як Unity, програміст займається майже виключно кроком програми та використовує мову високого рівня, таку як C #, на відміну від C або C ++. Нова сцена з усіма її примітивами, як правило, трикутниками, лініями та точками, переходить до наступного кроку в конвеєрі.
Прикладами завдань, які зазвичай виконуються на етапі програми, є методи виявлення зіткнень, анімація, морфінг та прискорення з використанням просторових схем підрозділу, таких як древо квадрантів чи дерево октантів. Вони також використовуються для зменшення обсягу основної пам'яті, необхідної в даний момент часу. "Світ" сучасної комп'ютерної гри набагато більший, ніж те, що могло б вписатись в пам'ять одразу.
Геометрія
Крок геометрії, який відповідає за більшість операцій з полігонами та їх вершинами, можна розділити на наступні п’ять завдань. Це залежить від конкретної реалізації того, як ці завдання організовані як фактичні паралельні кроки конвеєру.

Визначення
Вершина (множина: вершини) — точка у світі. Для з'єднання поверхонь використовується багато точок. В особливих випадках хмари точок малюються безпосередньо, але це все ж виняток.
Трикутник – найпоширеніший геометричний примітив комп’ютерної графіки. Він визначається його трьома вершинами і вектором нормалей — вектор служить для позначення передньої грані трикутника і є вектором, перпендикулярним поверхні. Трикутник може бути забезпечений кольором або текстурою (зображення "склеєне" зверху). Трикутники завжди існують в одній площині, тому вони віддають перевагу перед прямокутниками.
Світова система координат
Світова система координат – це система координат, в якій створюється віртуальний світ. Це повинно відповідати декільком умовам, щоб наступна математика була легко застосована:
- Це повинна бути прямокутна декартова система координат, у якій всі осі однаково масштабуються.
Як визначено одиницю системи координат, залишається розробнику. Від того, чи повинен одиничний вектор системи відповідати реально одному метру або Ангстремy, залежить від застосування.
- Використовувати декардовоі системи координат може визначати графічна бібліотека, яка буде використовуватися.
- Приклад: Якщо ми плануємо розробити тренажер польоту, ми можемо вибрати світову систему координат, щоб початок знаходився посередині землі, а одиниця була встановлена на один метр. Крім того, щоб полегшити посилання на реальність, ми визначаємо, що вісь X повинна перетинати екватор на нульовому меридіані, а вісь Z проходить через полюси. У правій системі вісь Y проходить через меридіан 90 ° – Схід (десь в Індійському океані). Тепер у нас є система координат, яка описує кожну точку на Землі у тривимірних декартових координатах. У цій системі координат ми зараз моделюємо принципи нашого світу, гір, долин та океанів.
- Примітка. Окрім комп’ютерної геометрії, для землі використовують географічні координати, тобто широту і довготу, а також висоту над рівнем моря. Орієнтовна конверсія – якщо не враховувати той факт, що земля не є точною сферою – проста:
- з R = радіус Землі [6.378.137m], lat = Широта, довга = Довгота, hasl = висота над рівнем моря.
- Усі наведені нижче приклади застосовуються у правій системі. Для системи з лівою рукою знаки можуть знадобитися замінити.
Об'єкти, що містяться в сцені (будинки, дерева, машини), часто проєктуються у власній системі об'єктів координат (також її називають модельною системою координат або локальною системою координат) з міркувань більш простого моделювання. Для присвоєння цим об'єктам координат у світовій системі координат або глобальній системі координат всієї сцени координати об'єкта перетворюються за допомогою перекладу, обертання або масштабування. Це робиться шляхом множення відповідних матриць переходу. Крім того, з одного об’єкта може бути сформовано кілька різнорідно перетворених копій, наприклад ліс з дерева.
Ця методика називається інстанцією.
- Для того, щоб розмістити модель літака у світі, ми спочатку визначаємо чотири матриці. Оскільки ми працюємо в тривимірному просторі, нам потрібні чотиривимірні однорідні матриці для наших розрахунків.
Спочатку нам потрібні три матриці обертання, а саме по одній для кожної з трьох осей літака (вертикальна вісь, поперечна вісь, поздовжня вісь).
- Навколо осі X (зазвичай визначається як поздовжня вісь у системі координат об'єкта)
- Навколо осі Y (зазвичай визначається як поперечна вісь в об'єктній системі координат)
- Навколо осі Z (зазвичай визначається як вертикальна вісь в системі об'єктів координат)
Ми також використовуємо матрицю перекладу, яка переміщує літальний апарат до потрібної точки нашого світу:
Тепер ми могли обчислити положення вершин літака у світових координатах, помноживши кожну точку послідовно на ці чотири матриці. Оскільки множення матриці з вектором є досить дорогим (забирає багато часу), зазвичай проходить інший шлях і спочатку множить чотири матриці разом. Множення двох матриць ще дорожче, але повинно бути виконане лише один раз для всього об’єкта. Множення і < рівнозначні. Після цього отримана матриця може бути застосована до вершин. На практиці, однак, множення з вершинами все ще не застосовується, але матриці камери – див. Нижче – визначаються спочатку.
Порядок застосування матриць є важливим, оскільки множення матриць не є комутативним. Це стосується також трьох обертів, як це можна продемонструвати на прикладі: Точка (1, 0, 0) лежить на осі X, якщо повернути її спочатку на 90 ° навколо X–, а потім навколо осі Y, він закінчується на осі Z (обертання навколо осі X не впливає на точку, яка знаходиться на осі). Якщо, з іншого боку, спершу обертається навколо осі Y, а потім навколо осі X, отримана точка розташована на осі Y. Сама послідовність довільна до тих пір, поки вона завжди однакова. Послідовність з x, то y, тоді z (рулон, крок, заголовок) часто найінтуїтивніша, оскільки обертання призводить до того, що напрямок компаса збігається з напрямком «носа».
Для визначення цих матриць також є дві конвенції, залежно від того, чи бажаєте ви працювати з векторами стовпців або векторами рядків. Тут різні графічні бібліотеки мають різні переваги. OpenGL віддає перевагу векторам стовпців, рядковим векторам DirectX. Рішення визначає, з якої сторони точкові вектори потрібно помножити на матриці перетворення. Для векторів стовпців множення виконується праворуч, тобто, де vout та vin 4x1 стовпчикові вектори. Зв'язування матриць також робиться справа наліво, тобто, наприклад , при першому обертанні, а потім перемиканні.
У випадку векторів рядків це працює саме навпаки. Зараз множення відбувається зліва як з векторами 1x4–рядків і конкатенація коли ми також спочатку обертаємося, а потім рухаємося. Матриці, показані вище, дійсні для другого випадку, тоді як ті для векторів стовпців переміщуються. Правило [3] застосовується, що для множення з векторами означає, що ви можете перемикати порядок множення, переміщуючи матрицю.
Цікавим у цьому ланцюжку матриць є те, що нова система координат визначається кожним таким перетворенням. Це можна продовжити за бажанням. Наприклад, гвинт літака може бути окремою моделлю, яка потім розміщується перекладом на ніс літака. У цьому перекладі потрібно лише описати перехід від модельної системи координат до системи координат гвинта. Для того, щоб намалювати весь літальний апарат, спочатку визначається матриця перетворення для літального апарату, точки трансформуються, а потім матриця моделі гвинта примножується на матрицю літака, а потім перетворюються точки гвинта.
Матриця, обчислена таким чином, також називається матрицею світу. Він повинен бути визначений для кожного об'єкта у світі до надання. Додаток може ввести тут зміни, наприклад змінити положення літака відповідно до швидкості після кожного кадру.
Перетворення камери
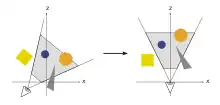
Окрім об'єктів, сцена також визначає віртуальну камеру чи переглядач, які вказують положення та напрямок перегляду, з якого повинна бути відображена сцена. Для спрощення подальшого проєктування та відсікання сцена перетворюється таким чином, що камера знаходиться біля початку, дивлячись вздовж осі Z. Отримана система координат називається системою координат камери, а перетворення називається трансформацією камери або переглядом трансформації.
- Матриця перегляду зазвичай визначається з положення камери, цільової точки (там, де дивиться камера) та "вектора вгору" ("вгору" з точки зору глядача). Спочатку потрібні три допоміжні вектори:
- Zaxis = нормальний (cameraPosition – cameraTarget)
- Xaxis = нормальний (крос (cameraUpVector, zaxis))
- Yaxis = хрест (zaxis, xaxis)
- При нормальному (v) = нормалізації вектора v;
- Вектор (v1, v2) = векторний добуток v1 і v2.
- Нарешті, матриця:
- з крапкою (v1, v2) = скалярний добуток v1 і v2.
Проєкція
Крок 3D–проєкції перетворює об'єм перегляду в куб з координатами кутових точок (–1, –1, 0) та (1, 1, 1); Інколи також використовуються інші цільові обсяги. Цей крок називається проєкцією, хоча він перетворює об'єм в інший об'єм, оскільки отримані Z координати не зберігаються на зображенні, а використовуються лише у Z-буферизації на наступному етапі растрування. У перспективній ілюстрації використовується центральна проєкція. Для обмеження кількості відображуваних об'єктів використовуються дві додаткові площини відсікання. Таким чином, візуальний об'єм є зрізаною пірамідою. Паралельна або ортогональна проєкція використовується, наприклад, для технічних зображень, оскільки вона має перевагу в тому, що всі паралелі в об'єктному просторі також є паралельними в просторі зображення, а поверхні та об'єми мають однаковий розмір незалежно від відстані від глядача. Карти використовують, наприклад, ортогональну проєкцію (так званий ортофотографія), але косі зображення пейзажу не можуть бути використані таким чином – хоча їх технічно можна зобразити, вони здаються такими спотвореними, що ми не можемо використовувати їх. Формула для обчислення матриці перспективного відображення:
- З h = cot (fieldOfView / 2.0) (кут діафрагми камери); w = h / аспектRatio (співвідношення сторін цільового зображення); поблизу = Найменша відстань, яку видно; далеко = Найдовша відстань, яку видно.
Причини, з яких тут потрібно надати найменшу та найбільшу відстань, – це, з одного боку, те, що ця відстань ділиться на, щоб досягти масштабування сцени (більш віддалені об'єкти менші за перспективним зображенням, ніж поблизу об’єктів), а з іншого боку, для масштабування значень Z до діапазону 0..1 для заповнення Z – буфера. Цей буфер часто має лише роздільну здатність 16 біт, тому значення близького та далекого значення слід вибирати ретельно. Занадто велика різниця між близьким і далеким значенням призводить до так званих Z–боїв через низьку роздільну здатність буфера Z –. З формули також видно, що близьке значення не може бути 0, оскільки ця точка є точкою фокусування проєкції. На даний момент немає жодної картини.
Для повноти формула паралельної проєкції (ортогональна проєкція):
- З w = ширина цільового куба (розмірність в одиницях світової системи координат); Н = w / аспектRatio (співвідношення сторін цільового зображення); поблизу = Найменша відстань, яку видно; далеко = Найдовша відстань, яку видно.
З метою ефективності матриця камери та проєкції зазвичай поєднується в матрицю перетворення, щоб система координат камери була опущена. Отримана матриця зазвичай однакова для одного зображення, тоді як світова матриця виглядає по–різному для кожного об'єкта. Тому на практиці огляд та проєкція попередньо розраховуються так, що під час відображення має бути адаптована лише світова матриця. Однак можливі і більш складні перетворення, такі як вершинне змішування. Також можуть бути виконані вільно програмовані шейдери геометрії, що змінюють геометрію.
На етапі фактичного відображення обчислюється матриця проєкції матриці світової матриці * камери *, а потім остаточно застосовується до кожної окремої точки. Таким чином, точки всіх об'єктів переносяться безпосередньо в систему координатних екранів (принаймні майже, діапазон значень осей все ще –1..1 для видимого діапазону, див. Розділ «Вікно – Відображення – Трансформація»).
Освітлення
Часто сцена містить джерела світла, розміщені в різних положеннях, щоб зробити освітлення предметів більш реалістичним. У цьому випадку коефіцієнт посилення текстури розраховується для кожної вершини на основі джерел світла та властивостей матеріалу, пов'язаних із відповідним трикутником. На пізньому етапі растерізації значення вершин трикутника інтерполюються над його поверхнею. На всі поверхні застосовується загальне освітлення (навколишнє світло). Це дифузна і, таким чином, напрямково–незалежна яскравість сцени. Сонце – це спрямоване джерело світла, яке можна вважати нескінченно далеко. Освітленість, здійснювана сонцем на поверхні, визначається формуванням скалярного добутку спрямованого вектора від сонця та нормального вектора поверхні. Якщо значення негативне, поверхня повернута до сонця.
Відсікання
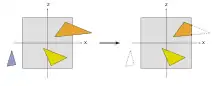
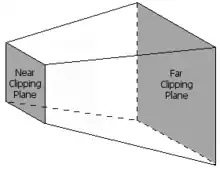
Тільки примітиви, що знаходяться у візуальному обсязі, насправді потрібно вирощувати (малювати). Цей візуальний об'єм визначається як внутрішня частина зрізаної піраміди, форма у вигляді піраміди із відрізаною верхівкою. Примітиви, які повністю знаходяться поза зоровим об'ємом, викидаються; Це називається випаданням зрізаної пераміди. Подальші способи відсікання, такі як зворотне відсікання, які зменшують кількість примітивів, які слід розглядати, теоретично можуть бути виконані на будь–якому етапі графічного конвеєра. Примітиви, які знаходяться лише частково всередині куба, повинні бути притиснутим до куба. Перевага попереднього кроку проєктування полягає в тому, що відсікання завжди відбувається проти одного куба. На остаточний крок пересилаються лише примітиви, можливо відрізані, які знаходяться у візуальному обсязі.
Перетворення вікна – перегляду
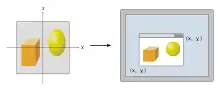
Для виведення зображення в будь–яку цільову область (вікно перегляду) екрану необхідно застосувати ще одне перетворення, перетворення Вікно – Перегляд. Це зсув з подальшим масштабуванням. Отримані координати – це координати пристрою вихідного пристрою. Вікно перегляду містить 6 значень: висота та ширина вікна у пікселях, лівий верхній кут вікна у координатах вікна (зазвичай 0, 0) та мінімальні та максимальні значення для Z (зазвичай 0 та 1).
- Формально:
- З vp = Viewport; v = Точка після проєкції
На сучасному обладнанні більшість етапів обчислення геометрії виконуються у вершинних шейдерах. Це, в принципі, вільно програмується, але, як правило, виконує принаймні перетворення точок і розрахунок освітленості. Для інтерфейсу програмування DirectX використання користувальницького вершинного шейдера необхідно з версії 10, тоді як для старих версій все ще є стандартний шейдер.
Растеризація
Етап растерізації є завершальним кроком перед фрагментом конвеєру шейдерів, що всі примітиви растрифіковані Pixel pipeline. На етапі растерізації створюються дискретні фрагменти із суцільних примітивів.
На цій стадії графічного конвеєра точки сітки також називають фрагментами, задля більшої виразності. Кожному фрагменту відповідає один піксель у буфері кадру, і це відповідає одному пікселю екрана. Вони можуть бути кольоровими (і, можливо, освітленими). Крім того, необхідно визначити видимий, ближчий до спостерігача фрагмент, у разі перекриття полігонів. Для цього так званого визначення прихованої поверхні визначення прихованої поверхні зазвичай використовується Z – буфер. Колір фрагмента залежить від освітленості, текстури та інших матеріальних властивостей видимого примітиву і часто інтерполюється за допомогою властивостей вершини трикутника. Якщо є, шейдер фрагмента (також званий Pixel Shader) виконується на етапі растрування для кожного фрагмента об'єкта. Якщо фрагмент видно, його тепер можна змішати з уже наявними значеннями кольорів на зображенні, якщо використовується прозорість або багатопробність. На цьому кроці один або кілька фрагментів перетворюються на піксель.
Щоб уникнути того, що користувач бачить поступову растеризацію примітивів, відбувається подвійна буферизація. Растеризація проводиться в спеціальній області пам’яті. Після того, як зображення було повністю растровано, воно копіюється у видиму область пам'яті зображення.
Зворотний
Усі використовувані матриці є неоднорідними і зворотніми. Оскільки множення двох невироджених матриць створює іншу несинулярну матрицю, вся матриця перетворення також є незворотною. Зворотний потрібен для перерахунку світових координат із координат екрану – наприклад, для визначення з позиції вказівника миші на клацається об’єкт. Однак оскільки екран і миша мають лише два виміри, третій невідомий. Тому промінь проєктується на положення курсора у світ і тоді визначається перетин цього променя з багатокутниками у світі.
Шейдер

Класичні відеокарти все ще відносно близькі до графічного конвеєра. Зі збільшенням вимог до GPU обмеження поступово знімалися, щоб створити більшу гнучкість. Сучасні відеокарти використовують вільно програмований конвеєр, керований шейдером, що дозволяє отримати прямий доступ до окремих етапів обробки. Щоб звільнити основний процесор, додаткові етапи обробки були переміщені до конвеєра та GPU.
Найважливішими шейдерними одиницями є піксельні шейдери, вершинні шейдери та шейдери з геометрії. Єдиний шейдер був введений для повного використання всіх одиниць. Це дає вам єдиний великий пул шейдерних одиниць. У міру необхідності басейн розділений на різні групи шейдерів. Тому суворе розділення між типами шейдерів більше не корисне.
Можна також використовувати так званий обчислювальний–шейдер для виконання будь–яких обчислень поза відображенням графіки на GPU. Перевага в тому, що вони працюють паралельно, але є обмеження. Ці універсальні обчислення також називаються обчисленнями загального призначення на графічних процесорах, або короткими GPGPU.
Дивись також
Джерела
- Tomas Akenine–Möller, Eric Haines: Real–Time Rendering. AK Peters, Natick, Mass. 2002, ISBN 1-56881-182-9.
- Michael Bender, Manfred Brill: Computergrafik: ein anwendungsorientiertes Lehrbuch. Hanser, München 2006, ISBN 3-446-40434-1.
- Fischer, Martin (4 липня 2011). Pixel-Fabrik. Wie Grafikchips Spielewelten auf den Schirm zaubern. c't Magazin für Computer Technik. Heise Zeitschriften Verlag. с. 180. ISSN 0724-8679.
Список літератури
- Lawrence, Jason (22 жовтня 2012). 3D Polygon Rendering Pipeline (PDF). web.archive.org. Архів оригіналу за 29 грудня 2016. Процитовано 19 вересня 2019.
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering, S. 11. (PDF)
- K. Nipp, D. Stoffer; Lineare Algebra; v/d/f Hochschulverlag der ETH Zürich; Zürich 1998, ISBN 3-7281-2649-7.