Коефіцієнт Джині
Коефіціє́нт Джи́ні — показник нерівності розподілу деякої величини чисел, що приймає значення між 0 і 1, де 0 означає абсолютну рівність (величина приймає лише одне значення), а 1 позначає повну нерівність. Найбільш відомим коефіцієнт є як міра нерівності доходів домогосподарств деякої країни чи регіону. Коефіцієнт Джині для доходів домогосподарств є найпопулярнішим показником економічної нерівності в країні.
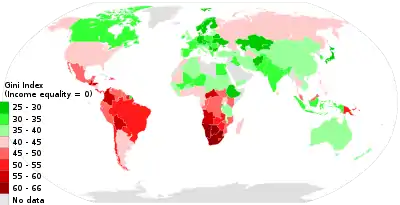
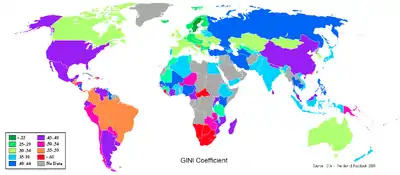
Окрім нерівності доходів, коефіцієнт Джині також рахують для нерівності багатства (майна і капіталу), ці два показники часто суттєво відрізняються[1].
Визначення
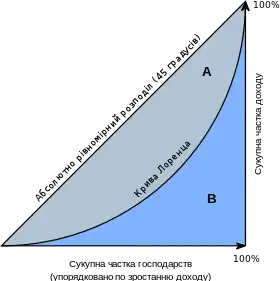
Коефіцієнт Джині найпростіше визначити за допомогою кривої Лоренца, що зображує частку величини y, що зосереджується на x% популяції з найменшим значенням цієї величини. Наприклад для розподілу доходів точка (20%, 10%) буде лежати на кривій Лоренца, якщо сукупний дохід двадцяти відсотків найбідніших домогосподарств рівний десяти відсоткам сукупного доходу усіх домогосподарств. Коефіцієнт Джині рівний відношенню площі області утвореної кривою Лоренца і прямою повної рівності (прямою під кутом 45°) до площі трикутника утвореного прямою повної рівності і прямими y = 0 x = 1. На малюнку перша область позначена сірим кольором, трикутник є об'єднанням фігур сірого і синього кольорів. Якщо позначити площі відповідних фігур 'A' і 'B' то можна записати формулу G=A/(A+B). Оскільки A+B = 0,5 то також справедлива формула G = 2· A = 1 — 2 · B.
Якщо весь дохід є рівномірно розподілений, то крива Лоренца збігається з прямою повної рівності і значення коефіцієнта Джині рівне нулю.
Обчислення
Якщо крива Лоренца задана у виді функції Y = L(X), то користуючись формулою G = 1 — 2 · B і визначенням площі фігури через інтеграл можна записати:
В багатьох випадках можна обчислити коефіцієнт Джині без прямого визначення кривої Лоренца. Наприклад якщо для деякої генеральної сукупності елементів відомі значення величини yi, i = 1 to n, причому (yi ≤ yi+1) то для обчислення коефіцієнта Джині можна використати формулу:
- Або простіше:
- Для дискретного розподілу з функцією ймовірностей f(y), де yi, i = 1 до n — точки з ненульовою ймовірністю, такі що (yi < yi+1) індекс Джині можна визначити за формулою:
- де
- and
- Для неперервного розподілу з кусково-диференційовною функцією розподілу F(y) рівною нулю для від'ємних значень, і скінченним середнім значенням μ коефіцієнт Джині рівний:
Часто проте точний вид кривої Лоренца не є відомим і доступною є лише інформація про частку Yk розподілу величини Y для частки Xk значень з найменшими значеннями змінної Y. Наприклад відомо загальна частка сукупного доходу для 10% найбідніших господарств, 20% найбідніших господарств і т. д. Тоді коефіцієнт Джині можна наближено обчислити за формулою Брауна:
Коефіцієнт Джині в країнах ЄС
Європейська статистична організація Євростат публікує щороку коефіцієнт Джині для кожної країни-члена ЄС. Наступна таблиця показує рейтинг станом на 2014 рік[2].
| Місце | Країна | Індекс Джині, % |
|---|---|---|
| 1 | Словаччина | 24,2 |
| 2 | Словенія | 24,4 |
| 3 | Чехія | 24,6 |
| 4 | Швеція | 24,9 |
| 5 | Нідерланди | 25,1 |
| 6 | Фінляндія | 25,4 |
| 7 | Бельгія | 25,9 |
| 8 | Австрія | 27 |
| 9 | Данія | 27,5 |
| 10 | Мальта | 27,9 |
| 11 | Угорщина | 28 |
| 12 | Німеччина | 29,7 |
| 13 | Ірландія | 30 |
| 14 | Франція | 30,1 |
| 15 | Велика Британія | 30,2 |
| 16 | Люксембург | 30,4 |
| 17 | Польща | 30,7 |
| 18 | Хорватія | 30,9 |
| 19 | Кіпр | 32,4 |
| 20 | Італія | 32,5 |
| 21 | Естонія | 32,9 |
| 22 | Іспанія | 33,7 |
| 23 | Румунія | 34 |
| 24 | Португалія | 34,2 |
| 25 | Греція | 34,4 |
| 26 | Литва | 34,6 |
| 27 | Латвія | 35,2 |
| 28 | Болгарія | 35,4 |
Коефіцієнт Джині в деяких країнах по всьому світу
Організація розвитку ООН ПРООН публікує огляди розподілу доходів у більшості країн світу (де дані надходять від Світового банку). Наступна таблиця є джерелом видання Організації Об'єднаних Націй в 2005 році (дані з окремих країн наведені в період 1993-2002 рр)
| Місце | Країна | Індекс Джині, % | Відношення сумарних доходів/витрат найбагатших 10% до найбідніших 10% | Відношення сумарних доходів/витрат найбагатших 20% до найбідніших 20% | Рік |
|---|---|---|---|---|---|
| 1 | Данія | 24.7 | 8.1 | 4.3 | 2000 |
| 2 | Японія | 24.9 | 4.5 | 3.4 | 1993 |
| 3 | Швеція | 25 | 6.2 | 4 | 2000 |
| 4 | Чехія | 25.4 | 5.2 | 3.5 | 1996 |
| 5 | Норвегія | 25.8 | 6.1 | 3.9 | 2000 |
| 6 | Словаччина | 25.8 | 6.7 | 4 | 1996 |
| 7 | Боснія і Герцоговина | 26.2 | 5.4 | 3.8 | 2001 |
| 8 | Угорщина | 26.9 | 5.5 | 3.8 | 2002 |
| 9 | Фінляндія | 26.9 | 5.6 | 3.8 | 2000 |
| 10 | Україна | 28.1 | 5.9 | 4.1 | 2006 |
| 11 | Німеччина | 28.3 | 6.9 | 4.3 | 2000 |
| 12 | Словенія | 28.4 | 5.9 | 3.9 | 1998 |
| 13 | Хорватія | 29 | 7.3 | 4.8 | 2003 |
| 14 | Австрія | 29.1 | 6.9 | 4.4 | 2004 |
| 15 | Болгарія | 29.2 | 7 | 4.4 | 2005 |
| 16 | Білорусь | 29.7 | 6.9 | 4.5 | 2002 |
| 17 | Ефіопія | 30 | 6.6 | 4.3 | 2000 |
| 20 | Нідерланди | 30.9 | 9.2 | 5.1 | 1999 |
| 21 | Румунія | 31 | 7.5 | 4.9 | 2003 |
| 24 | Канада | 32.6 | 9.4 | 5.5 | 2000 |
| 26 | Франція | 32.7 | 9.1 | 5.6 | 2004 |
| 28 | Бельгія | 33 | 8.2 | 4.9 | 2000 |
| 32 | Швейцарія | 33.7 | 9 | 5.5 | 2000 |
| 40 | Польща | 34.5 | 8.8 | 5.6 | 2002 |
| 43 | Іспанія | 34.7 | 10.3 | 6 | 2000 |
| 44 | Австралія | 35.2 | 12.5 | 7 | 1994 |
| 49 | Велика Британія | 36 | 13.8 | 7.2 | 1999 |
| 50 | Нова Зеландія | 36.2 | 12.5 | 6.8 | 1997 |
| 53 | Індія | 36.8 | 8.3 | 5.6 | 2004 |
| 58 | Йорданія | 38.8 | 11.3 | 6.9 | 2003 |
| 63 | Ізраїль | 39.2 | 13.4 | 7.9 | 2005 |
| 65 | Марокко | 39.5 | 11.7 | 7.2 | 1999 |
| 67 | Росія | 39.9 | 12.7 | 7.6 | 2002 |
| 73 | США | 40.8 | 15.9 | 8.4 | 2007 |
| 79 | Сінгапур | 42.5 | 17.7 | 9.7 | 1998 |
| 89 | Ямайка | 45.5 | 17.3 | 9.8 | 2004 |
| 93 | КНР | 46.9 | 21.6 | 12.2 | 2004 |
| 107 | Аргентина | 51.3 | 40.9 | 17.8 | 2007 |
| 116 | Бразилія | 57 | 51.3 | 21.8 | 2004 |
| 117 | ПАР | 57.8 | 33.1 | 17.9 | 2000 |
| 122 | Ботсвана | 60.5 | 43 | 20.4 | 1993 |
| 123 | Лесото | 63.2 | 105 | 44.2 | 2002 |
| 124 | Намібія | 74.3 | 128.8 | 56.1 | 2003 |
Див. також
Примітки
- Майкл Робертс. Багатство чи дохід? // Спільне, 27 серпня 2020
- Gini coefficient of equivalised disposable income - EU-SILC survey
Література
- Рождєственська Л. Г. Статистика ринку товарів і послуг: Навч. посіб. — К.: КНЕУ, 2005. — 419 с. ISBN 966-574-691-Х
- Ха-Юн Чанґ. Економіка. Інструкція з використання: Пер. з англ. - К. Наш Формат, 2016. - 400с. - іл. ISBN 978-617-7279-42-5