Кількості інформації

Шеннон вивів міру інформаційного вмісту, названу власною інформацією (англ. self-information) або «несподіваністю» (англ. "surprisal") повідомлення ${\displaystyle m}$:

${\displaystyle \operatorname {I} (m)=\log \left({\frac {1}{p(m)}}\right)=-\log(p(m))\,}$

де ${\displaystyle p(m)=\mathrm {Pr} (M=m)}$ є ймовірністю обрання повідомлення ${\displaystyle m}$ з усіх можливих варіантів вибору в просторі повідомлень ${\displaystyle M}$. Основа логарифму впливає лише на коефіцієнт масштабування, і, відтак, на одиниці, в яких виражається вимірюваний інформаційний вміст. Якщо основою логарифму є 2, то міра інформації виражається в одиницях бітів.

Інформація передається з джерела до отримувача лише якщо отримувач цієї інформації ще не мав її заздалегідь. Повідомлення, які передають інформацію, що відбувається напевно, і вже відома отримувачеві, реальної інформації не містять. Повідомлення, що трапляються нечасто, містять більше інформації, ніж повідомлення, які трапляються частіше. Цей факт віддзеркалено в наведеному вище рівнянні — незмінне повідомлення, тобто, з імовірністю 1, має нульову міру інформації. Крім того, складене повідомлення з двох (або більше) не пов'язаних (або взаємно незалежних) повідомлень матиме міру інформації, яка є сумою мір інформації кожного з повідомлень окремо. Цей факт також віддзеркалено в наведеному вище рівнянні, що підтверджує обґрунтованість його виведення.

Приклад. Повідомлення прогнозу погоди: «Прогноз на ніч: Темно. Тривала темрява, аж до широко розсіяного світла вранці.» Це повідомлення майже не містить інформації. Проте прогноз хуртовини безумовно міститиме інформацію, оскільки таке не трапляється щовечора. Величина інформації буде ще більшою в точному прогнозі снігу для теплого місця, такого як Маямі. Величина інформації в прогнозі снігу для місця, де сніг не йде ніколи (неможлива подія), є найвищою (нескінченність).

Ентропія (англ. entropy) дискретного простору повідомлень ${\displaystyle M}$ є мірою величини невизначеності (англ. uncertainty), що ми маємо стосовно того, яке повідомлення буде обрано. Її визначено як усереднену власну інформацію повідомлення ${\displaystyle m}$ з цього простору повідомлень:

${\displaystyle \mathrm {H} (M)=\mathbb {E} \left[\operatorname {I} (M)\right]=\sum _{m\in M}p(m)\operatorname {I} (m)=-\sum _{m\in M}p(m)\log p(m).}$

де

${\displaystyle \mathbb {E} [-]}$ позначує операцію математичного сподівання (англ. expected value).

Важливою властивістю ентропії є те, що вона є найбільшою, коли всі повідомлення в просторі повідомлень є рівноймовірними (тобто, ${\displaystyle p(m)=1/|M|}$). В цьому випадку ${\displaystyle \mathrm {H} (M)=\log |M|}$.

Іноді функцію ${\displaystyle \mathrm {H} }$ виражають в термінах імовірностей розподілу:

${\displaystyle \mathrm {H} (p_{1},p_{2},\ldots ,p_{k})=-\sum _{i=1}^{k}p_{i}\log p_{i},}$ де кожна ${\displaystyle p_{i}\geq 0}$ та ${\displaystyle \sum _{i=1}^{k}p_{i}=1.}$

Важливим особливим випадком цього є функція двійкової ентропії:

${\displaystyle \mathrm {H} _{\mbox{b}}(p)=\mathrm {H} (p,1-p)=-p\log p-(1-p)\log(1-p).\,}$

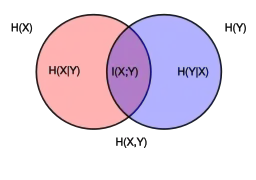
Спільну ентропію (англ. joint entropy) двох дискретних випадкових змінних ${\displaystyle X}$ та ${\displaystyle Y}$ визначають як ентропію їхнього спільного розподілу:

${\displaystyle \mathrm {H} (X,Y)=\mathbb {E} _{X,Y}\left[-\log p(x,y)\right]=-\sum _{x,y}p(x,y)\log p(x,y)\,}$

Якщо ${\displaystyle X}$ та ${\displaystyle Y}$ є незалежними, то ця спільна ентропія є просто сумою їхніх окремих ентропій.

(Зауваження: Спільну ентропію не слід плутати з перехресною ентропією, незважаючи на подібний запис.)

За заданого конкретного значення випадкової змінної ${\displaystyle Y}$ умовну ентропію ${\displaystyle X}$ за ${\displaystyle Y=y}$ визначено як

${\displaystyle \mathrm {H} (X|y)=\mathbb {E} _{\left[X|Y\right]}[-\log p(x|y)]=-\sum _{x\in X}p(x|y)\log p(x|y)}$

де ${\displaystyle p(x|y)={\frac {p(x,y)}{p(y)}}}$ є умовною ймовірністю ${\displaystyle x}$ за заданого ${\displaystyle y}$.

Умовну ентропію (англ. conditional entropy) ${\displaystyle X}$ за заданого ${\displaystyle Y}$, що також називають ухильністю (англ. equivocation) ${\displaystyle X}$ від ${\displaystyle Y}$, задають як

${\displaystyle \mathrm {H} (X|Y)=\mathbb {E} _{Y}\left[\mathrm {H} \left(X|y\right)\right]=-\sum _{y\in Y}p(y)\sum _{x\in X}p(x|y)\log p(x|y)=\sum _{x,y}p(x,y)\log {\frac {p(y)}{p(x,y)}}.}$

Вона використовує умовне математичне сподівання з теорії імовірності.

Базовою властивістю умовної ентропії є те, що

${\displaystyle \mathrm {H} (X|Y)=\mathrm {H} (X,Y)-\mathrm {H} (Y).\,}$

Відстань Кульбака — Лейблера (або розходження інформації, приріст інформації, або відносна ентропія, англ. Kullback–Leibler divergence, information divergence, information gain, relative entropy) є способом порівнювання двох розподілів, «істинного» розподілу ймовірності ${\displaystyle p}$ та довільного розподілу ймовірності ${\displaystyle q}$. Якщо ми стискаємо дані таким чином, який передбачає, що ${\displaystyle q}$ є розподілом, що лежить в основі якихось даних, тоді як насправді правильним розподілом є ${\displaystyle p}$, то відстань Кульбака — Лейблера є числом усереднених додаткових бітів над рівнем, необхідних для стискання, або, математично,

${\displaystyle D_{\mathrm {KL} }{\bigl (}p(X)\|q(X){\bigr )}=\sum _{x\in X}p(x)\log {\frac {p(x)}{q(x)}}.}$

В якомусь сенсі вона дійсно є «відстанню» від ${\displaystyle q}$ до ${\displaystyle p}$, хоча вона й не є справжньою метрикою через те, що вона не є симетричною.

Виявляється, що однією з найкорисніших та найважливіших мір інформації є взаємна інформація (англ. mutual information), або передавана інформація (англ. transinformation). Вона є мірою того, як багато інформації може бути отримано про одну випадкову змінну шляхом спостерігання іншої. Взаємну інформацію ${\displaystyle X}$ відносно ${\displaystyle Y}$ (яка концептуально представляє усереднену величину інформації про ${\displaystyle X}$, яку можна здобути спостеріганням ${\displaystyle Y}$) задають як

${\displaystyle \operatorname {I} (X;Y)=\sum _{y\in Y}p(y)\sum _{x\in X}{p(x|y)\log {\frac {p(x|y)}{p(x)}}}=\sum _{x,y}p(x,y)\log {\frac {p(x,y)}{p(x)\,p(y)}}.}$

Основною властивістю взаємної інформації є те, що

${\displaystyle \operatorname {I} (X;Y)=\mathrm {H} (X)-\mathrm {H} (X|Y).\,}$

Тобто, знаючи ${\displaystyle Y}$, ми можемо заощадити в середньому ${\displaystyle \operatorname {I} (X;Y)}$ бітів у кодуванні ${\displaystyle X}$, у порівнянні з незнанням ${\displaystyle Y}$. Взаємна інформація є симетричною:

${\displaystyle \operatorname {I} (X;Y)=\operatorname {I} (Y;X)=\mathrm {H} (X)+\mathrm {H} (Y)-\mathrm {H} (X,Y).\,}$

Взаємну інформацію можливо виразити як усереднену відстань Кульбака — Лейблера (приріст інформації) апостеріорного розподілу ймовірності ${\displaystyle X}$ за заданого значення ${\displaystyle Y}$ відносно апріорного розподілу ймовірності ${\displaystyle X}$:

${\displaystyle \operatorname {I} (X;Y)=\mathbb {E} _{p(y)}\left[D_{\mathrm {KL} }{\bigl (}p(X|Y=y)\|p(X){\bigr )}\right].}$

Іншими словами, вона є мірою того, наскільки в середньому зміниться розподіл ймовірності ${\displaystyle X}$, якщо ми отримаємо значення ${\displaystyle Y}$. Обчислюють її часто як розходження між добутком відособлених розподілів та справжнім спільним розподілом:

${\displaystyle \operatorname {I} (X;Y)=D_{\mathrm {KL} }{\bigl (}p(X,Y)\|p(X)p(Y){\bigr )}.}$

Взаємна інформація є тісно пов'язаною з перевіркою логарифмічним відношенням правдоподібностей в контексті таблиць спряженості та мультиноміального розподілу, та з критерієм χ² Пірсона: взаємну інформацію можливо розглядати як статистику для оцінювання незалежності в парі змінних, і вона має добре визначений асимптотичний розподіл.

Основні міри дискретної ентропії було аналогічно розширено на неперервні простори шляхом заміни сум інтегралами, та функцій маси ймовірності функціями густини ймовірності. І хоча в обох випадках взаємна інформація виражає число бітів інформації, спільне для цих двох джерел, ця аналогія не передбачає однакових властивостей: наприклад, диференціальна ентропія може бути від'ємною.

Диференціальні аналоги ентропії, спільної ентропії, умовної ентропії та взаємної інформації визначено таким чином:

${\displaystyle h(X)=-\int _{X}f(x)\log f(x)\,dx}$

${\displaystyle h(X,Y)=-\int _{Y}\int _{X}f(x,y)\log f(x,y)\,dx\,dy}$

${\displaystyle h(X|y)=-\int _{X}f(x|y)\log f(x|y)\,dx}$

${\displaystyle h(X|Y)=\int _{Y}\int _{X}f(x,y)\log {\frac {f(y)}{f(x,y)}}\,dx\,dy}$

${\displaystyle \operatorname {I} (X;Y)=\int _{Y}\int _{X}f(x,y)\log {\frac {f(x,y)}{f(x)f(y)}}\,dx\,dy}$

де ${\displaystyle f(x,y)}$ є функцією густини спільного розподілу, ${\displaystyle f(x)}$ та ${\displaystyle f(y)}$ є відособленими розподілами, а ${\displaystyle f(x|y)}$ є умовним розподілом.

• Теорія інформації