Умовна ентропія
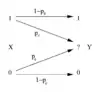
В теорії інформації умо́вна ентропі́я (або ухи́льність, англ. conditional entropy, equivocation) — це оцінка кількості інформації, необхідної, щоб описати вихід випадкової змінної , враховуючи, що значення іншої випадкової змінної є відомим. Тут інформація вимірюється в шеннонах, натах або гартлі. Ентропія , обумовлена записується як .
| Теорія інформації |
|---|
 |
|
|
|
Означення
Нехай є ентропією дискретної випадкової змінної , обумовленою набуванням дискретною випадковою змінною певного значення . Нехай має функцію маси ймовірності . Безумовна ентропія обчислюється як , тобто,
де є інформаційним вмістом набування результатом значення . Ентропію , обумовлену набуванням випадковою змінною значення , визначено аналогічно до умовного математичного сподівання:
є результатом усереднювання над усіма можливими значеннями , що їх може набувати .
Для заданих дискретних випадкових змінних з носієм та з носієм умовну ентропію відносно визначають як зважену суму для кожного з можливих значень із застосуванням як вагових коефіцієнтів:[1]
Примітка: Зрозуміло, що вирази та для фіксованих слід вважати рівними нулеві.
Властивості
Нульова умовна ентропія
якщо і лише якщо значення повністю визначається значенням .
Умовна ентропія незалежних випадкових змінних
І навпаки, якщо і лише якщо та є незалежними випадковими змінними.
Ланцюгове правило
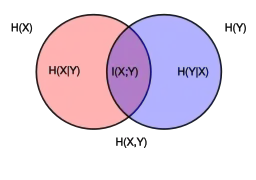
Припустімо, що об'єднана система, яку визначають дві випадкові змінні та , має спільну ентропію , тобто, нам потрібно в середньому біт інформації, щоби описати її точний стан. Тепер, якщо ми спочатку дізналися значення , ми отримали біт інформації. Щойно стало відомим, нам потрібно лише біт, щоб описати стан системи в цілому. Ця величина в точності дорівнює , що дає нам ланцюгове правило умовної ентропії:
Ланцюгове правило випливає з вищенаведеного означення умовної ентропії:
В загальному випадку ланцюгове правило для декількох випадкових змінних стверджує, що
Воно має вигляд, подібний до ланцюгового правила в теорії ймовірностей, за винятком того, що замість множення використовується додавання.
Правило Баєса
Правило Баєса для умовної ентропії стверджує, що
Доведення. і . Через симетрію, . Віднімання цих двох рівнянь має наслідком правило Баєса.
Якщо є умовно незалежною від за заданої , то ми маємо
Інші властивості
Для будь-яких та
де є взаємною інформацією та .
Для незалежних та
- та
Хоча конкретно-умовна ентропія і може бути або меншою, або більшою за для заданої випадкової варіати змінної , але ніколи не може перевищувати .
Умовна диференціальна ентропія
Означення
Наведене вище означення є для дискретних випадкових змінних, але в випадку неперервних випадкових змінних воно чинним не є. Неперервну версію дискретної умовної ентропії називають умовною диференціальною (або неперервною) ентропією (англ. conditional differential (continuous) entropy). Нехай та є неперервними випадковими змінними з функцією густини спільної ймовірності . Диференціальну умовну ентропію означують як
- .[1]
Властивості
На противагу до умовної ентропії дискретних випадкових змінних, умовна диференціальна ентропія може бути від'ємною.
Як і в дискретному випадку, для диференціальної ентропії існує ланцюгове правило:
Зауважте, проте, що це правило може не виконуватися, якщо залучені диференціальні ентропії не існують, або є нескінченними.
Спільну диференціальну ентропію також використано в означенні взаємної інформації між неперервними випадковими змінними:
, з рівністю якщо і лише якщо та є незалежними.[1]
Стосунок до похибки оцінювача
Умовна диференціальна ентропія дає нижню межу математичного сподівання квадратичної похибки оцінювача. Для будь-якої випадкової змінної , спостереження та оцінювача виконується наступне:[1]
Це стосується принципу невизначеності в квантовій механіці.
Узагальнення до квантової теорії
У квантовій теорії інформації умовна ентропія узагальнюється до умовної квантової ентропії. Остання, на відміну від свого класичного аналога, може набувати від'ємних значень.
Див. також
- Інформаційна ентропія
- Взаємна інформація
- Умовна квантова ентропія
- Різновидність інформації
- Нерівність ентропійної потужності
- Функція правдоподібності
Примітки
- T. Cover; J. Thomas (1991). Elements of Information Theory. ISBN 0-471-06259-6. (англ.)
