Категорія (математика)

Категорія у математиці — це алгебраїчна структура подібна до групи, але від якої не вимагається властивість обернення або замикання. Вона містить «об'єкти», що сполучаються «стрілками». Категорія має дві основні властивості: можливість компонувати стрілки асоціативним чином і існування стрілки тотожності для кожного об'єкта. Простим прикладом категорії для множин, об'єктами якої є множини, а стрілки позначають функції.

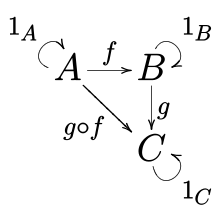
Це приклад категорії із колекцією об'єктів A, B, C і колекцією морфізмів, що позначена f, g, g ∘ f, а петлі є стрілками тотожності.

Теорія категорій — це гілка математики, яка досліджує і узагальнює усю математику в термінах категорій, незалежно від того що собою представляють стрілки. Практично кожну галузь сучасної математики можна описати в термінах категорій, і часто це дозволяє виявити глибокі закономірності і подібність між, з першого погляду різними, галузями математики. Як така, теорія категорій утворює в математиці альтернативну основу для теорії множин та інших аксіоматично побудованих основ. В загальному випадку, об'єкти і стрілки можуть бути будь-якими абстрактними поняттями, і така нотація категорій дозволяє мати фундаментальний абстрактний спосіб описати математичні сутності і їх зв'язки.

Крім математики, теорія категорій використовується для формалізації багато інших систем в комп'ютерних науках, наприклад для описання семантики мов програмування.

Дві категорії є однаковими якщо вони мають однакову колекцію об'єктів, однакову колекцію стрілок, і однаковий асоціативний метод утворення будь-якої пари стрілок. Дві різні категорії також можуть бути «еквівалентними» в рамках теорії категорій, навіть якщо вони не мають точно однакової структури.

Існує ряд добре відомих категорій, які можуть мати загальні назви і скорочення описанні жирним шрифтом: наприклад Set — категорія множин і функцій; Ring — категорія кілець і їх гомоморфізмів; і Top — категорія топологічних просторів і неперервних відображень. Всі наведені категорії мають тотожне відображення, що є стрілкою тотожності і композицію, що є асоціативною операцією над стрілками.

Будь-який моноїд можна розуміти як особливий вид категорій (з одним єдиним об'єктом чиї самоморфізми представлені елементами моноїда), що може мати будь-який передпорядок.

Історія

Теорія категорій вперше з'явилася в статі під назвою «General Theory of Natural Equivalences», написаній Самуелем Ейленбергом та Сандерсом мак Лейном в 1945.[1]

Визначення

Існує декілька еквівалентних визначень поняття категорії.[2] Одним із найчастіше вживаних визначень є наступне. Категорія C складається з

  • класу об'єктів ob(C)
  • класу hom(C) морфізмів, або стрілок, або функцій відображення, між об'єктами. Кожен морфізм f має вхідний об'єкт a і вихідний об'єкт b де a і b знаходяться в класі ob(C). Прийнято записувати f: a → b, що озвучують як, те що «f є морфізмом із a у b». Прийнято записувати hom(a, b) (або homC(a, b) якщо може бути неоднозначність щодо того, до якої категорії відноситься hom(a, b)) аби позначити hom-class всіх морфізмів із a у b. (Деякі автори позначають як Mor(a, b) або просто C(a, b).)
  • для будь-яких трьох об'єктів a, b і c, бінарна операція hom(a, b) × hom(b, c) → hom(a, c) називається композицією морфізмів; композиція із f : a → b і g : b → c буде записуватися як g ∘ f або gf.

такі, для яких виконуються наступні аксіоми:

  • (Асоціативність) якщо f : a → b, g : b → c і h : c → d тоді h ∘ (g ∘ f) = (h ∘ g) ∘ f, і
  • (Тотожність) для кожного об'єкту x, існує морфізм 1x : x → x (іноді позначають як idx), що називається морфізмом тотожності для x, такий що для кожного морфізму f : a → x і кожного морфізму g : x → b, ми матимемо 1x ∘ f = f і g ∘ 1x = g.

Великі і малі категорії

Категорія C називається малою, якщо ob(C) і hom(C) насправді є множинами, а не класами, а великі навпаки.

Примітки
  1. S. Eilenberg and S. Mac Lane «General Theory of Natural Equivalences», Transactions of The American Mathematical Society 01/1945; 58(2):231-231. DOI:10.2307/1990284
  2. Barr & Wells, Chapter 1.

Література
  • Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990). Abstract and Concrete Categories. John Wiley & Sons. ISBN 0-471-60922-6. (now free on-line edition, GNU FDL).
  • Asperti, Andrea; Longo, Giuseppe (1991). Categories, Types and Structures. MIT Press. ISBN 0-262-01125-5..
  • Awodey, Steve (2006). Category theory. Oxford logic guides 49. Oxford University Press. ISBN 978-0-19-856861-2..
  • Barr, Michael; Wells, Charles (2005). Toposes, Triples and Theories. Reprints in Theory and Applications of Categories 12 (вид. revised). MR 2178101..
  • Borceux, Francis (1994). Handbook of Categorical Algebra. Encyclopedia of Mathematics and its Applications. 50–52. Cambridge: Cambridge University Press. ISBN 0-521-06119-9..
  • Hazewinkel, Michiel, ред. (2001). Category. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
  • Herrlich, Horst; Strecker, George E. (2007). Category Theory. Heldermann Verlag..
  • Jacobson, Nathan (2009). Basic algebra (вид. 2nd). Dover. ISBN 978-0-486-47187-7..
  • Lawvere, William; Schanuel, Steve (1997). Conceptual Mathematics: A First Introduction to Categories. Cambridge: Cambridge University Press. ISBN 0-521-47249-0..
  • Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics 5 (вид. 2nd). Springer-Verlag. ISBN 0-387-98403-8..
  • Marquis, Jean-Pierre (2006). Category Theory. У Zalta, Edward N. Stanford Encyclopedia of Philosophy..
  • Sica, Giandomenico (2006). What is category theory?. Advanced studies in mathematics and logic 3. Polimetrica. ISBN 978-88-7699-031-1..
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.