Зовнішня похідна
Зовнішня похідна у диференціальній геометрії розширює поняття диференціала функції, що є диференціальною формою нульового порядку, на довільні форми вищих порядків. В сучасному виді поняття зовнішньої похідної було введено французьким математиком Елі Картаном.
Зовнішня похідна d має властивість, що d2 = 0 і вона використовується для визначення когомології де Рама на диференціальних формах. Інтегрування форм надає природний гомоморфізм з когомології де Рама на сингулярні когомології гладких многовидів. Згідно з теоремою де Рама це відображення є ізоморфізмом.
Визначення
Аксіоматичне визначення
Нехай — множина диференціальних k-форм на гладкому многовиді M. Лінійне відображення називається зовнішньою похідною якщо:
- Для воно збігається зі звичайним диференціалом функції;
- Для будь-якої форми виконується рівність .
Для довільного гладкого многовиду відображення з даними властивостями існує і є єдиним.
Визначення за допомогою локальних координат
Для довільної точки існує окіл цієї точки і координатні функції такі що довільну диференціальну k-форму можна записати як
для деяких гладких функцій визначених в цьому околі. Тоді зовнішня похідна в цій точці рівна
Інваріантна формула
Якщо — гладкі векторні поля на многовиді, тоді зовнішня похідна визначається за формулою:
де символ ^ у виразі означає, що вказане векторне поле не є аргументом відповідної диференціальної форми, а позначає дужки Лі векторних полів.
Якщо є афінною зв'язністю із нульовим крученням на многовиді, тобто то зовнішню похідну можна також записати за допомогою оператора коваріантної похідної:
Ця рівність є справедливою, зокрема для зв'язності Леві-Чивіти у рімановій геометрії.
Приклади
- 1
Нехай σ = u dx1∧dx2 у базисі 1-форм dx1,...,dxn. Зовнішня похідна цієї диференціальної форми рівна:
- 2
Для 1-форми σ = u dx + v dy визначеної у R2 з використанням попереднього одержується:
Властивості
Якщо ƒ: M → N — гладке відображення і Ωk — гладкий контраваріантний функтор що присвоює кожному гладкому многовиду множину k-форм на цьому многовиді тоді наступна діаграма комутує:
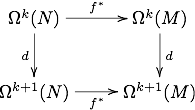
тобто d(ƒ*ω) = ƒ*dω, де ƒ* позначає зворотне відображення від ƒ. Отже, d є природним відображенням з Ωk на Ωk+1.
Література
- Картан А. Дифференциальное исчисление. Дифференциальные формы. — М.: Мир, 1971.
- Isadore Singer and John A. Thorpe, Lecture Notes on Elementary Geometry and Topology, Springer-Verlag (1967) ISBN 0-387-90202-3