Квадратне рівняння

• Рівняння виду ${\displaystyle ax^{2}=0}$ рівносильне рівнянню ${\displaystyle x^{2}=0}$ і тому завжди має тільки один корінь ${\displaystyle x=0}$.
• Рівняння виду ${\displaystyle ax^{2}+bx=0}$ розв'язується винесенням за дужки ${\displaystyle x}$: ${\displaystyle x(ax+b)=0}$. Таке рівняння має два корені: ${\displaystyle x_{1}=0,x_{2}=-b/a}$
• Квадратне рівняння виду ${\displaystyle ax^{2}+c=0}$ рівносильне рівнянню ${\displaystyle x^{2}=-c/a}$. Якщо ${\displaystyle -c/a>0}$, воно має два дійсних розв'язки, якщо ${\displaystyle -c/a<0}$ — жодного дійсного. Отже, якщо знаки коефіцієнтів різні, то ${\displaystyle -c/a}$ додатнє і рівняння має два корені. Якщо знаки коефіцієнтів однакові, число ${\displaystyle -c/a}$ від'ємне і ${\displaystyle ax^{2}+c=0}$ не має дійсних коренів.

Повні квадратні рівняння розв'язуються за допомогою дискриміна́нта (лат. diskriminans — розрізняючий), який позначається латинською літерою ${\displaystyle D}$.

Помноживши обидві частини рівняння ${\displaystyle ax^{2}+bx+c=0}$ на ${\displaystyle 4a}$, дістанемо:

${\displaystyle 4a^{2}x^{2}+4axb+4ac=0}$,

${\displaystyle (2ax)^{2}+4axb+b^{2}-b^{2}+4ac=0}$

і далі за формулою скороченого множення отримаємо

${\displaystyle (2ax+b)^{2}=b^{2}-4ac}$.

Права частина цього виразу і є дискримінантом:

${\displaystyle D=b^{2}-4ac}$

Якщо ${\displaystyle D>0}$, то квадратне рівняння рівносильне рівнянню ${\displaystyle (2ax+b)^{2}=\left({\sqrt {D}}\right)^{2}}$, звідки

${\displaystyle 2ax+b={\sqrt {D}},\qquad x={\frac {-b+{\sqrt {D}}}{2a}},}$

або

${\displaystyle 2ax+b=-{\sqrt {D}},\qquad x={\frac {-b-{\sqrt {D}}}{2a}}.}$

У цьому випадку дане рівняння має два корені, які відрізняються лише знаком перед ${\displaystyle {\sqrt {D}}}$. Коротко ці корені записують так:

${\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}}$, де ${\displaystyle D=b^{2}-4ac\qquad (1).}$

Якщо ${\displaystyle D=0}$, то ${\displaystyle 2ax+b=0}$, звідки ${\displaystyle x=-{\frac {b}{2a}}}$ — єдиний корінь (точніше — два однакові корені)

У випадку, якщо дискримінант менший за нуль, то дане рівняння не має дійсних коренів. Але при цьому є можливість знайти два комплексних корені за формулою (1) або, скориставшись наступною формулою, щоб не добувати корінь з від'ємного числа:

${\displaystyle x_{1,2}={\frac {-b\pm i\cdot {\sqrt {-b^{2}+4ac}}}{2a}}.}$

Якщо коефіцієнти в рівнянні мають великі числові значення для уникнення довгих розрахунків можна скористатися формулою:

${\displaystyle x_{1,2}={\frac {-k\pm {\sqrt {k^{2}-ac}}}{a}},}$ де :${\displaystyle k={\frac {b}{2}}.}$

Приклад:

${\displaystyle 2x^{2}+3x-5=0.}$

${\displaystyle a=2}$ ${\displaystyle b=3}$ ${\displaystyle c=-5}$

${\displaystyle D=3^{2}-4\cdot 2\cdot (-5)=9+40=49=7^{2}}$

У цьому випадку дане рівняння має два корені, які відрізняються лише знаком перед ${\displaystyle {\sqrt {D}}}$

${\displaystyle x_{1}={\frac {-3-7}{4}}=-2,5}$

${\displaystyle x_{2}={\frac {-3+7}{4}}=1}$

Якщо рівняння ${\displaystyle x^{2}+px+q=0}$ має корені ${\displaystyle x_{1}}$ і ${\displaystyle x_{2},}$ то їх можна знаходити за формулами:

${\displaystyle x_{1}={\frac {-p-{\sqrt {p^{2}-4q}}}{2}}}$ і ${\displaystyle x_{2}={\frac {-p+{\sqrt {p^{2}-4q}}}{2}}.}$

При додаванні та множенні коренів отримуємо відповідно:

${\displaystyle x_{1}+x_{2}={\frac {-p-{\sqrt {p^{2}-4q}}}{2}}+{\frac {-p+{\sqrt {p^{2}-4q}}}{2}}=-p,}$

${\displaystyle x_{1}\cdot x_{2}={\frac {-p-{\sqrt {p^{2}-4q}}}{2}}*{\frac {-p+{\sqrt {p^{2}-4q}}}{2}}=q.}$

Якщо сума і добуток чисел ${\displaystyle m}$ і ${\displaystyle n}$ дорівнюють відповідно ${\displaystyle -p}$ і ${\displaystyle q}$, то ${\displaystyle m}$ і ${\displaystyle n}$ — корені рівняння ${\displaystyle x^{2}+px+q=0.}$

Використовуючи теорему Вієта можна перевіряти правильність розв'язання квадратних рівнянь. А користуючись оберненою теоремою, можна навіть усно розв'язувати більшість зведених рівнянь. Для прикладу розв'яжемо таке рівняння:

${\displaystyle 2x^{2}+16x+14=0.}$

Щоб звести рівняння поділимо його на 2 (незведене рівняння матиме такі ж корені, як і зведене)

${\displaystyle x^{2}+8x+7=0.}$

Оскільки 7 (вільний член) — це добуток коренів рівняння, то коренями має бути пара чисел 7 та 1 або −7 та −1. Так як сума коренів дорівнює −8 (другий коефіцієнт з протилежним знаком), то шукана пара — −7 і −1. Отже:

${\displaystyle x_{1}=-7,\quad x_{2}=-1.}$

Графік функції y = x² − x − 2 перетинає вісь абсцис у точках з координатами, що дорівнюють кореням рівняння x² − x − 2 = 0

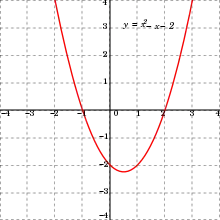
Корені рівняння

${\displaystyle ax^{2}+bx+c=0}$

є також нулями функції

${\displaystyle f(x)=ax^{2}+bx+c.}$

В точках перетину її графіка з віссю абсцис значення x-координати дорівнюватиме кореням рівняння. У випадку, коли дискримінант цього рівняння більший нуля, графік перетинається з віссю у двох точках; коли ${\displaystyle D=0}$, графік дотикається до неї в одній точці; якщо ж дискримінант менший за нуль, графік не перетинає вісь Ox взагалі.

Ліва частина квадратного рівняння, яка також називається квадратним тричленом, може бути розкладена на множники за такою формулою:
${\displaystyle ax^{2}+bx+c=a(x-x_{1})(x-x_{2})}$, де ${\displaystyle x_{1},x_{2}}$ — корені цього рівняння.

В процесі доповнення до квадрата використовують алгебраїчне рівняння

${\displaystyle x^{2}+2hx+h^{2}=(x+h)^{2},}$

яке визначає чітко визначений алгоритм, який можна використати для розв'язку квадратного рівняння.[2] Розпочнемо із квадратного рівняння наступної форми, ax² + bx + c = 0

1. Розділимо кожну його частину на a, коефіцієнт при квадратному члені рівняння.
2. Віднімемо сталу c/a з обох частин рівняння.
3. Додайте квадрат половини значення b/a, коефіцієнта при x, до обох частин рівняння. Це "доповнює квадрат", перетворюючи ліву частину у ідеальний квадрат.
4. Перепишіть ліву частину у вигляді квадрата і спростіть праву частину при необхідності.
5. Отримаємо два лінійні рівняння прирівнявши квадратний корінь у лівій частині із додатнім і від'ємним квадратним коренями правої частини.
6. Знайдемо розв'язок двох лінійних рівнянь.

Наведемо приклад роботи алгоритма, розв'язавши рівняння 2x² + 4x − 4 = 0

${\displaystyle 1)\ x^{2}+2x-2=0}$

${\displaystyle 2)\ x^{2}+2x=2}$

${\displaystyle 3)\ x^{2}+2x+1=2+1}$

${\displaystyle 4)\ \left(x+1\right)^{2}=3}$

${\displaystyle 5)\ x+1=\pm {\sqrt {3}}}$

${\displaystyle 6)\ x=-1\pm {\sqrt {3}}}$

Подвійний знак плюс-мінус "±" означає, що обидва варіанти x = −1 + √3 і x = −1 − √3 є розв'язками квадратного рівняння.[3]