Марковський процес вирішування
Ма́рковські проце́си вирі́шування (МПВ, англ. Markov decision process, MDP) забезпечують математичну систему для моделювання ухвалення рішень у ситуаціях, в яких наслідки є частково випадковими, а частково контрольованими ухвалювачем рішення. МПВ є корисними для дослідження широкого спектра задач оптимізації, розв'язуваних динамічним програмуванням та навчанням з підкріпленням. МПВ були відомі щонайменше з 1950-х років (пор. Bellman, 1957). Основна маса досліджень марковських процесів вирішування стала результатом книги Рональда Говарда, опублікованої 1960 року, «Динамічне програмування та марковські процеси» (англ. Dynamic Programming and Markov Processes).[1] Їх застосовують у широкій області дисциплін, включно з робототехнікою, автоматизованим керуванням, економікою та виробництвом.
Якщо точніше, то марковський процес вирішування є стохастичним процесом керування дискретного часу. На кожному кроці часу процес перебуває в якомусь стані , і ухвалювач рішення може обрати будь-яку дію , доступну в стані . Процес реагує на наступному кроці часу випадковим переходом до нового стану і наданням ухвалювачеві рішення відповідної винагороди (англ. reward) .
Ймовірність переходу процесу до його нового стану знаходиться під впливом обраної дії. Конкретно, вона задається функцією переходу стану . Таким чином, наступний стан залежить від поточного стану та від дії ухвалювача рішення . Але для заданих та він є умовно незалежним від усіх попередніх станів та дій; іншими словами, переходи станів процесу МПВ задовольняють марковську властивість.
Марковські процеси вирішування є розширенням марковських ланцюгів; різниця полягає в доданні дій (що дає вибір) та винагород (що дає мотивацію). І навпаки, якщо для кожного стану існує лише одна дія (наприклад, «чекати») та всі винагороди є однаковими (наприклад, «нуль»), то марковський процес вирішування зводиться до марковського ланцюга.
Визначення
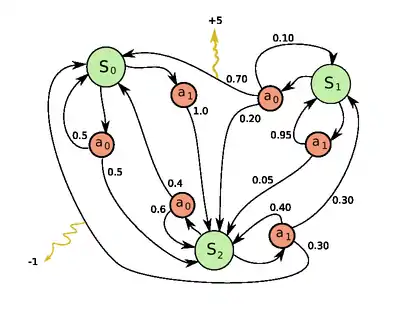
Марковський процес вирішування є 5-кою , де
- є скінченною множиною станів,
- є скінченною множиною дій (як альтернатива, є скінченною множиною дій, доступних зі стану ),
- є ймовірністю того, що дія в стані в момент часу призведе до стану в момент часу ,
- є безпосередньою винагородою (або очікуваною безпосередньою винагородою), отримуваною після переходу до стану зі стану ,
- є коефіцієнтом знецінювання (англ. discount factor), який представляє відмінність важливості майбутніх та поточних винагород.
(Зауваження: Теорія марковських процесів вирішування не стверджує, що чи є скінченними, але основні алгоритми, наведені нижче, передбачають, що вони є скінченними.)
Задача
Основною задачею МПВ є знайти «стратегію» (англ. policy) для ухвалювача рішень: функцію , яка визначає дію , яку ухвалювач рішення обере в стані . Зауважте, що щойно марковський процес вирішування поєднано таким чином зі стратегією, то це фіксує дію для кожного стану, і отримане в результаті поєднання поводиться як марковський ланцюг.
Метою є обрати таку стратегію , яка максимізуватиме деяку кумулятивну функцію випадкових винагород, зазвичай — очікувану знецінену функцію над потенційно нескінченним горизонтом:
- (де ми обираємо )
де є коефіцієнтом знецінювання, і задовольняє . (Наприклад, , де інтенсивністю знецінювання є .) Зазвичай є близьким до 1.
Завдяки марковській властивості, оптимальну стратегію для цієї конкретної задачі насправді може бути записано як функцію лише від , як і передбачалося вище.
Алгоритми
МПВ може бути розв'язувано лінійним програмуванням, або динамічним програмуванням. Далі ми представимо останній підхід.
Припустімо, що ми знаємо функцію переходу стану та функцію винагороди , і хочемо обчислити стратегію, яка максимізує очікувану знецінену винагороду.
Стандартне сімейство алгоритмів для обчислення цієї оптимальної стратегії вимагає зберігання двох масивів, проіндексованих за станом: цінностей (англ. value) , який містить дійсні значення, та стратегії , який містить дії. По завершенню алгоритму, міститиме розв'язок, а міститиме знецінену суму винагород, яку буде зароблено (в середньому) при слідуванні цим розв'язком зі стану .
Алгоритм має наступні два види кроків, які повторюються в певному порядку для всіх станів, допоки подальших змін вже не відбуватиметься. Вони визначаються рекурсивно наступним чином:
Їхній порядок залежить від варіанту алгоритму; можна робити їх одночасно для всіх станів, або стан за станом, і частіше для одних станів, ніж для інших. Якщо жоден зі станів не виключатиметься назавжди з будь-якого з кроків, то алгоритм зрештою прийде до правильного розв'язку.
Ітерація за цінностями
В ітерації за цінностями (англ. value iteration, Bellman, 1957), яку також називають зворотною індукцією, функція не використовується; натомість значення обчислюється в межах за потребою. Метод ітерації за цінностями для МПВ увійшов до праці Ллойда Шеплі 1953 року про стохастичні ігри[2] як окремий випадок, але це було визнано лише згодом.[3]
Підставлення обчислення до обчислення дає поєднаний крок:
де є номером ітерації. Ітерація за цінностями починається з та як припущення про функцію цінності. Потім виконується ітерування з повторним обчисленням для всіх станів , поки не збіжиться, коли ліва сторона дорівнюватиме правій (що є «рівнянням Беллмана» для цієї задачі).
Ітерація за стратегіями
В ітерації за стратегіями (англ. policy iteration, Howard, 1960) перший крок виконується один раз, а потім другий крок повторюється до збіжності. Потім перший крок виконується знову, і так далі.
Замість повторювання другого кроку до збіжності його може бути сформульовано та розв'язано як набір лінійних рівнянь.
Цей варіант має перевагу в тому, що існує чітка умова зупинки: коли масив не змінюється в процесі застосування кроку 1 до всіх станів, алгоритм завершується.
Видозмінена ітерація за стратегіями
У видозміненій ітерації за стратегіями (англ. modified policy iteration, van Nunen, 1976, Puterman & Shin, 1978) перший крок виконується один раз, а потім другий крок повторюється кілька разів. Потім знову перший крок виконується один раз, і так далі.
Пріоритетне підмітання
В цьому варіанті (англ. prioritized sweeping) кроки застосовуються до станів із надаванням переваги тим, які є якимось чином важливими — чи то на основі алгоритму (нещодавно були великі зміни в або навколо цих станів), чи то на основі використання (ці стани знаходяться близько до початкового стану, або іншим чином становлять інтерес для особи або програми, яка застосовує цей алгоритм).
Розширення та узагальнення
Марковський процес вирішування є стохастичною грою з лише одним гравцем.
Часткова спостережуваність
Детальніші відомості з цієї теми ви можете знайти в статті Частково спостережуваний марковський процес вирішування.
Наведене вище розв'язання передбачає, що в той момент, коли треба вирішувати, яку дію вчинити, стан є відомим; інакше обчислено бути не може. Якщо це припущення не є вірним, задачу називають частково спостережуваним марковським процесом вирішування (ЧСМПВ, англ. partially observable Markov decision process, POMDP).
Головний поступ у цій області було забезпечено Бурнетасом та Катехакісом в «Оптимальних адаптивних стратегіях для марковських процесів вирішування».[4] В цій праці було побудовано клас адаптивних стратегій, які володіють властивостями рівномірно максимального темпу збіжності для загальної очікуваної винагороди скінченного інтервалу, за припущень скінченних просторів стан-дія та нескоротності закону переходу. Ці стратегії приписують, щоби вибір дій на кожному стані в кожен момент часу ґрунтувався на показниках, які є роздуваннями правої сторони рівнянь оптимальності очікуваної усередненої винагороди.
Навчання з підкріпленням
Якщо ймовірності винагород є невідомими, то задача є задачею навчання з підкріпленням (Sutton та Barto, 1998).
Для цього корисно визначити наступну функцію, яка відповідає вчиненню дії з продовженням оптимальним чином (або відповідно до будь-якої наявної в даний момент стратегії):
І хоча ця функція також є невідомою, досвід під час навчання ґрунтується на парах (разом з наслідком ; тобто, «Я був у стані , спробував вчинити , і сталося »). Таким чином, є масив , і досвід використовується для його безпосереднього уточнення. Це відоме як Q-навчання.
Навчання з підкріпленням може розв'язувати марковські процеси вирішування без явного вказання ймовірностей переходів; значення ймовірностей переходів необхідні для ітерації за цінностями та за стратегіями. В навчанні з підкріпленнями замість явного вказання ймовірностей переходів доступ до них отримується через імітатор, який зазвичай багаторазово перезапускається з рівномірного випадкового початкового стану. Навчання з підкріпленням також може поєднуватися з наближенням функцій, щоби можна було братися за задачі з дуже великим числом станів.
Автомати з самонавчанням
Детальніші відомості з цієї теми ви можете знайти в статті Автомати з самонавчанням.
Ще одне застосування процесу МПВ в теорії машинного навчання називається автоматами з самонавчанням. Воно також є одним із типів навчання з підкріпленням, якщо середовище має стохастичний характер. Перше детальне дослідження про автомати з самонавчанням (англ. learning automata) здійснили Нарендра та Татачар (1974), в якому їх було первісно описано явно як скінченні автомати.[5] Подібно до навчання з підкріпленням, алгоритм автоматів із самонавчанням також має перевагу розв'язання задач, у яких імовірності або винагороди є невідомими. Відмінність автоматів із самонавчанням від Q-навчання полягає в тому, що вони не включають пам'ять Q-значень, а для знаходження результату навчання уточнюють ймовірності дій безпосередньо. Автомати з самонавчанням є однією зі схем навчання з суворим доведенням збіжності.[6]
В теорії автоматів із самонавчанням стохастичний автомат (англ. stochastic automaton) складається з:
- множини можливих входів x,
- множини можливих внутрішніх станів Φ = { Φ1, …, Φs },
- множини можливих виходів, або дій, α = { α1, …, αr }, де r≤s,
- вектора початкової ймовірності станів p(0) = ≪ p1(0), …, ps(0) ≫,
- обчислюваної функції A, яка після кожного кроку часу t породжує p(t+1) з p(t), поточного входу та поточного стану, і
- функції G: Φ → α, яка породжує вихід на кожному кроці часу.
Стани такого автомату відповідають станам «марковського процесу дискретного часу з дискретними параметрами».[7] На кожному кроці часу t=0,1,2,3,… автомат читає вхід зі свого середовища, уточнює P(t) до P(t+1) за допомогою A, випадково обирає наступний стан відповідно до ймовірностей P(t+1) та виводить відповідну дію. Середовище автомата, в свою чергу, читає цю дію, і надсилає автоматові наступний вхід.[6]
Інтерпретація в термінах теорії категорій
Крім як через винагороди, марковський процес вирішування можна розуміти і в термінах теорії категорій. А саме, нехай позначає вільний моноїд з породжувальною множиною . Нехай позначає категорію Клайслі монади Жирі. Тоді функтор кодує як множину станів , так і функцію ймовірностей .
Таким чином, марковський процес вирішування може бути узагальнено з моноїдів (категорій з одним об'єктом) на довільні категорії. Результат можна назвати контекстно-залежним марковським процесом вирішування (англ. context-dependent Markov decision process), оскільки перехід від одного об'єкту до іншого в змінює множину доступних дій та множину можливих станів.
Марковський процес вирішування безперервного часу
В марковських процесах вирішування дискретного часу рішення здійснюються через дискретні проміжки часу. Проте для марковських процесів вирішування безперервного часу (англ. Continuous-time Markov Decision Processes) рішення можуть здійснюватися в будь-який час, який обере ухвалювач рішень. У порівнянні з марковськими процесами вирішування дискретного часу, марковські процеси вирішування безперервного часу можуть краще моделювати процес ухвалювання рішень для системи, яка має безперервну динаміку, тобто системи, динаміка якої визначається диференціальними рівняннями з частинними похідними.
Визначення
Для обговорення марковських процесів вирішування безперервного часу введімо два набори позначень:
Якщо простір станів та простір дій є скінченними,
- : простір станів (англ. State space);
- : простір дій (англ. Action space);
- : , функція інтенсивності переходів (англ. transition rate function);
- : , функція винагороди (англ. reward function).
Якщо простір станів та простір дій є неперервними,
- : простір станів (англ. state space);
- : простір можливого керування (англ. space of possible control);
- : , функція інтенсивності переходів (англ. transition rate function);
- : , функція інтенсивності винагороди (англ. reward rate function), така, що , де є функцією винагороди, яку ми обговорювали в попередньому випадку.
Задача
Як і в марковських процесах вирішування дискретного часу, в марковському процесі вирішування безперервного часу ми хочемо знаходити оптимальну стратегію (англ. policy) або керування (англ. control), яке давало би нам оптимальну очікувану проінтегровану винагороду:
Де
Формулювання лінійного програмування
Якщо простори станів та дій є скінченними, то для пошуку оптимальної стратегії ми можемо використовувати лінійне програмування, що було одним із найперших застосованих підходів. Тут ми розглядаємо лише ергодичну модель, яка означає, що наш МПВ безперервного часу стає ергодичним марковським ланцюгом безперервного часу за сталої стратегії. За цього припущення, хоча ухвалювач рішення і може здійснювати рішення в будь-який час у поточному стані, він не може виграти більше, здійснюючи більше ніж одну дію. Для нього краще здійснювати дію лише в той момент часу, коли система переходить з поточного стану до іншого. За деяких умов (детальніше див. Наслідок 3.14 у Continuous-Time Markov Decision Processes), якщо наша функція оптимальної цінності є незалежною від стану , то ми матимемо наступну нерівність:
Якщо існує функція , то буде найменшим , яке задовольняє наведене вище рівняння. Щоби знаходити , ми можемо застосовувати наступну модель лінійного програмування:
- Пряма лінійна програма (П-ЛП, англ. primal linear program, P-LP)
- Двоїста лінійна програма (Д-ЛП, англ. dual linear program, D-LP)
є придатним розв'язком Д-ЛП, якщо є невиродженою, і задовольняє обмеження задачі Д-ЛП. Придатний розв'язок Д-ЛП називають оптимальним розв'язком, якщо
для всіх придатних розв'язків Д-ЛП . Щойно ми знайшли оптимальний розв'язок , ми можемо використовувати його для встановлення оптимальних стратегій.
Рівняння Гамільтона — Якобі — Беллмана
Якщо простір станів та простір дій в МПВ безперервного часу є неперервними, то оптимальний критерій можна знаходити шляхом розв'язання диференціального рівняння Гамільтона — Якобі — Беллмана (ГЯБ, англ. Hamilton–Jacobi–Bellman equation, HJB) в часткових похідних. Для обговорення рівняння ГЯБ нам необхідно переформулювати нашу задачу:
є функцією остаточної винагороди (англ. terminal reward function), є вектором стану системи, є вектором керування системою, який ми намагаємося знайти. показує, як стан системи змінюється з часом. Рівняння Гамільтона — Якобі — Беллмана є таким:
Ми можемо розв'язувати це рівняння, щоби знаходити оптимальне керування , яке давало би нам оптимальну цінність
Застосування
Марковські процеси вирішування безперервного часу мають застосування в системах масового обслуговування, процесах епідемії та процесах населення.
Альтернативні позначення
Термінологія та позначення МПВ не є остаточно узгодженими. Є дві основні течії — одна зосереджується на задачах максимізації з контекстів на кшталт економіки, застосовуючи терміни дія (англ. action), винагорода (англ. reward), цінність (англ. value), та називаючи коефіцієнт знецінювання (англ. discount factor) або , в той час як інша зосереджується на задачах мінімізації з техніки та навігації, застосовуючи терміни керування (англ. control), витрати (англ. cost), остаточні витрати (англ. cost-to-go), і називаючи коефіцієнт знецінювання (англ. discount factor) . На додачу, різниться й позначення ймовірності переходу.
| в цій статті | альтернативне | коментар |
|---|---|---|
| дія | керування | |
| винагорода | витрати | є від'ємною |
| цінність | остаточні витрати | є від'ємною |
| стратегія | стратегія | |
| коефіцієнт знецінювання | коефіцієнт знецінювання | |
| ймовірність переходу | ймовірність переходу |
На додачу, ймовірність переходу іноді записують як , або, рідше, як .
Обмежені марковські процеси вирішування
Обмежені марковські процеси вирішування (ОМПВ, англ. Constrained Markov Decision Process, CMDP) є розширеннями марковських процесів вирішування (МПВ). Між МПВ та ОМПВ є три докорінні відмінності.[8]
- Після застосування дії замість однієї витрати несуться декілька витрат.
- ОМПВ розв'язуються лише за допомогою лінійних програм, а динамічне програмування не працює.
- Остаточна стратегія залежить від початкового стану.
Існує ряд застосувань ОМПВ. Нещодавно їх було застосовано в сценаріях планування руху в робототехніці.[9]
Див. також
- Ймовірнісні автомати
- Квантові скінченні автомати
- Частково спостережуваний марковський процес вирішування
- Динамічне програмування
- Рівняння Беллмана для застосувань в економіці.
- Рівняння Гамільтона — Якобі — Беллмана
- Оптимальне керування
- Рекурсивна економіка
- Задача про мабіногіонських овець
- Стохастичні ігри
- Q-навчання
Примітки
Джерела
- Bellman, R. (1957). A Markovian Decision Process. Journal of Mathematics and Mechanics 6. (англ.)
- Bellman., R. E. (2003). Dynamic Programming (вид. Dover paperback edition). Princeton, NJ: Princeton University Press. ISBN 0-486-42809-5. Проігноровано невідомий параметр
|orig-year=(довідка) (англ.) - Howard, Ronald A. (1960). Dynamic Programming and Markov Processes. The M.I.T. Press. (англ.)
- Shapley, Lloyd (1953). Stochastic Games. Proceedings of National Academy of Science 39: 1095–1100. (англ.)
- Kallenberg, Lodewijk (2002). Finite state and action MDPs. У Feinberg, Eugene A.; Shwartz, Adam. Handbook of Markov decision processes: methods and applications. Springer. ISBN 0-7923-7459-2. (англ.)
- Bertsekas, D. (1995). Dynamic Programming and Optimal Control 2. MA: Athena. (англ.)
- Burnetas, A.N.; Katehakis, M. N. (1997). Optimal Adaptive Policies for Markov Decision Processes. Mathematics of Operations Research 22 (1): 222. doi:10.1287/moor.22.1.222. (англ.)
- Feinberg, E.A.; Shwartz, A., ред. (2002). Handbook of Markov Decision Processes. Boston, MA: Kluwer. (англ.)
- Derman, C. (1970). Finite state Markovian decision processes. Academic Press. (англ.)
- Puterman., M. L. (1994). Markov Decision Processes. Wiley. (англ.)
- Tijms., H.C. (2003). A First Course in Stochastic Models. Wiley. (англ.)
- Sutton, R. S.; Barto, A. G. (1998). Reinforcement Learning: An Introduction. Cambridge, MA: The MIT Press. Архів оригіналу за 11 грудня 2013. Процитовано 8 вересня 2016. (англ.)
- van Nunen, J.A. E. E (1976). A set of successive approximation methods for discounted Markovian decision problems. Z. Operations Research 20: 203–208. (англ.)
- Narendra, K. S.; Thathachar, M. A. L. (1 липня 1974). Learning Automata - A Survey. IEEE Transactions on Systems, Man, and Cybernetics. SMC-4 (4): 323–334. ISSN 0018-9472. doi:10.1109/TSMC.1974.5408453. (англ.)
- Narendra, Kumpati S.; Thathachar, Mandayam A. L. (1989). Learning automata: An introduction (англ.). Prentice Hall. ISBN 9780134855585. (англ.)
- Meyn, S. P. (2007). Control Techniques for Complex Networks. Cambridge University Press. ISBN 978-0-521-88441-9. Архів оригіналу за 19 червня 2010. Додаток містить скорочену Meyn & Tweedie. Архів оригіналу за 18 грудня 2012. (англ.)
- Ross, S. M. (1983). Introduction to stochastic dynamic programming. Academic press. (англ.)
- Guo, X.; Hernández-Lerma, O. (2009). Continuous-Time Markov Decision Processes. Springer. (англ.)
- Puterman, M. L.; Shin, M. C. (1978). Modified Policy Iteration Algorithms for Discounted Markov Decision Problems. Management Science 24. (англ.)
- Altman, Eitan (1999). Constrained Markov decision processes 7. CRC Press. (англ.)
- Feyzabadi, S.; Carpin, S. (18-22 Aug 2014). Risk-aware path planning using hierarchical constrained Markov Decision Processes. Automation Science and Engineering (CASE) IEEE International Conference. с. 297,303. (англ.)
Посилання
- MDP Toolbox для MATLAB, GNU Octave, Scilab та R Інструментарій марковських процесів вирішування (МПВ).
- MDP Toolbox для Matlab — Чудовий навчальний посібник та інструментарій Matlab для роботи з МПВ. (англ.)
- Інструментарій МПВ для Python Пакет для розв'язання МПВ
- Reinforcement Learning[недоступне посилання з квітня 2019] Введення від Річарда Саттона та Ендрю Барто (англ.)
- SPUDD Структурований розв'язувач МПВ для завантаження від Jesse Hoey
- Learning to Solve Markovian Decision Processes від Satinder P. Singh (англ.)
- Optimal Adaptive Policies for Markov Decision Processes від Burnetas та Katehakis (1997). (англ.)