Матриця повороту

• Оскільки поворот — це перетворення координат, при якому зберігаються довжини векторів, то ${\displaystyle (x^{\prime })^{T}\cdot x^{\prime }=x^{T}R^{T}\cdot Rx=x^{T}\cdot x,}$

отже, матриця повороту є ортогональною матрицею:

${\displaystyle \ R^{-1}=R^{T}}$ (обернена матриця дорівнює транспонованій матриці).

• Оскільки поворот зберігає орієнтацію, то

${\displaystyle \ \det R=+1}$ (детермінант матриці повороту дорівнює одиниці).

• Добутком матриць повороту є матриця повороту:

${\displaystyle (R_{1}R_{2})^{T}(R_{1}R_{2})=R_{2}^{T}(R_{1}^{T}R_{1})R_{2}=I,}$

${\displaystyle \ \det(R_{1}R_{2})=(\det R_{1})(\det R_{2})=+1.}$

Три вищеперераховані властивості означають, що матриці повороту утворюють дійсну спеціальну ортогональну групу (SO(n)).

• Корисною є властивість взаємодії з векторним добутком:

${\displaystyle R({\vec {a}}\times {\vec {b}})=R{\vec {a}}\times R{\vec {b}}.}$

Поворот в площині на кут ${\displaystyle \varphi }$ переводить точку ${\displaystyle (x,y)}$ в точку ${\displaystyle (x',y')}$

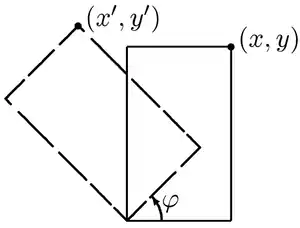
У двовимірному випадку матриця повороту має вигляд

${\displaystyle R(\varphi )={\begin{bmatrix}\cos \varphi &-\sin \varphi \\\sin \varphi &\cos \varphi \end{bmatrix}},}$

де ${\displaystyle \varphi }$ — кут повороту проти годинникової стрілки.

Вона обертає вектор рядок за допомогою наступного множення матриць,

${\displaystyle {\begin{bmatrix}x'\\y'\\\end{bmatrix}}={\begin{bmatrix}\cos \varphi &-\sin \varphi \\\sin \varphi &\cos \varphi \\\end{bmatrix}}{\begin{bmatrix}x\\y\\\end{bmatrix}}}$.

Тож нові координати (x',y') точки (x,y) після обертання будуть наступні:

${\displaystyle x'=x\cos \varphi -y\sin \varphi \,}$,

${\displaystyle y'=x\sin \varphi +y\cos \varphi \,}$.

• Матриці повороту відносно осей x, y та z відповідно:

${\displaystyle R_{x}(\varphi )={\begin{bmatrix}1&0&0\\0&\cos \varphi &-\sin \varphi \\0&\sin \varphi &\cos \varphi \\\end{bmatrix}},\qquad R_{y}(\varphi )={\begin{bmatrix}\cos \varphi &0&\sin \varphi \\0&1&0\\-\sin \varphi &0&\cos \varphi \\\end{bmatrix}},\qquad R_{z}(\varphi )={\begin{bmatrix}\cos \varphi &-\sin \varphi &0\\\sin \varphi &\cos \varphi &0\\0&0&1\\\end{bmatrix}}.}$

• Матриця повороту може бути виражена через кути Ейлера як

${\displaystyle \ R=R_{z}(\varphi )\cdot R_{y}(\theta )\cdot R_{x}(\psi ).}$

• Матриця повороту відносно одиничного вектора ${\displaystyle \mathbf {u} =(x,y,z)}$ на кут ${\displaystyle \varphi }$:

${\displaystyle R_{\mathbf {u} }(\varphi )=\mathbf {uu} ^{T}+(I-\mathbf {uu} ^{T})\cos \varphi +{\big [}\mathbf {u} {\big ]}_{\times }\sin \varphi ,}$

де

${\displaystyle {\big [}\mathbf {u} {\big ]}_{\times }}$ — матриця векторного добутку,

${\displaystyle \mathbf {u\otimes u} =\mathbf {uu} ^{T}}$ — тензорний добуток векторів (результатом є матриця).

Кожен з трьох доданків є ортогональним до двох інших:

перший — проектор на лінію вектора u,

інші — на лінії, що перпендикулярні вектору u.

Вищенаведена формула — матричний запис формули повороту Родрігеса.

У просторі Мінковського матриця повороту включає в себе як просторові повороти, так і переходи від однієї інерційної системи відліку до іншої, які задаються перетвореннями Лоренца.

• Кватерніони і повороти простору
• Унітарна матриця

• Weisstein, Eric W. Матриця повороту(англ.) на сайті Wolfram MathWorld.

• Гантмахер Ф. Р. Теория матриц. — 2 изд. — Москва : Наука, 1967. — 576 с. — ISBN 5-9221-0524-8.(рос.)