Тензорний добуток

Тензорний добуток — операція над лінійними просторами, а також над елементами (векторами, матрицями, операторами, тензорами тощо) просторів, що перемножуються.

Тензорний добуток лінійних просторів $A$ і $B$ є лінійний простір, що позначається $A\otimes B$ , для елементів $a\in A$ і $b\in B$ , їх тензорний добуток $a\otimes b$ лежить у просторі $A\otimes B$ .

Позначення тензорного добутку виникло аналогічно позначенню декартового добутку множин.

Тензорний добуток векторних просторів

Скінченновимірні простори

Нехай $A$ і $B$ — скінченновимірні векторні простори над полем $K$ , $\{e_{i}\}_{i=1\dots n}$ — базис в $A$ , $\{f_{k}\}_{k=1\dots m}$ — базис в $B$ . Тензорним добутком $A\otimes B$ просторів $A$ і $B$ будемо називати векторний простір, породжений елементами $e_{i}\otimes f_{k}$ , що називаються тензорними добутками базисних векторів. Тензорний добуток $a\otimes b$ довільних векторів $a\in A,~b\in B$ можна визначати, вважаючи операцію $\otimes$ білінійною:

(\lambda a_{1}+\mu a_{2})\otimes b=\lambda \,a_{1}\otimes b+\mu \,a_{2}\otimes b,~~\lambda ,\mu \in K

a\otimes (\lambda b_{1}+\mu b_{2})=\lambda \,a\otimes b_{1}+\mu \,a\otimes b_{2},~~\lambda ,\mu \in K

При цьому тензорний добуток довільних векторів $a$ і $b$ виражається як лінійна комбінація базисних векторів $e_{i}\otimes f_{k}$ . Елементи у $A\otimes B$ , що представляються у вигляді $a\otimes b$ , називаються розкладними.

Хоча тензорних добуток просторів визначається через набір базисів, його геометричні властивості не залежать від цього вибору.

Функторіальність

Тензорний добуток — це в деякому сенсі найзагальніший простір, в який можна білінійно відобразити вихідні простори. А саме, для будь-якого іншого простору $C$ і білінійного відображення $\otimes ^{\prime }:A\times B\to C$ існує єдиний гомоморфізм $f:A\otimes B\to C$ такий, що

\otimes ^{\prime }=f\circ \otimes

Зокрема, звідси слідує, що тензорний добуток не залежить від вибору базисів в $A$ і $B$ , оскільки всі простори, які при цьому отримуються $A\otimes B$ виявляються канонічно ізоморфні.

Таким чином, довільне білінійне відображення $L^{2}\ni \varphi :A\times B\to C$ може бути визначене як лінійне відображення $L\ni \varphi :A\otimes B\to C$ , при чому достатньо задати його лише на добутку базисних векторів.

Простори $\ L^{2}(A\times B,C)$ і $L(A\otimes B,C)$ є канонічно ізоморфними.

Іншими словами, довільний функтор $\otimes :C\times C\rightarrow C$ називається тензорним добутком. Нехай $C$ - категорія із тензорним добутком $\otimes .$ Умовою асоціативності для $\otimes$ є ізоморфізм

${\displaystyle \vartheta$

Тому для будь-якої трійки $A,B,C$ об'єктів категорії $C$ є ізоморфізм

$\vartheta _{A,B,C}:(A\otimes B)\otimes C\rightarrow A\otimes (B\otimes C),$

такий, що діаграма

є комутативною для морфізмів $f,g,h$ категорії $C$ .

Тензорні категорії аналогічні супералгебрам Хопфа.

Часткові випадки

Тензорний добуток двох векторів

(Матричний) добуток вектора-стовпчика справа на вектор-рядок дає їх тензорний добуток:

\mathbf {a} \otimes \mathbf {b} ^{\textsf {T}}\rightarrow {\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\\a_{4}\end{bmatrix}}{\begin{bmatrix}b_{1}&b_{2}&b_{3}\end{bmatrix}}={\begin{bmatrix}a_{1}b_{1}&a_{1}b_{2}&a_{1}b_{3}\\a_{2}b_{1}&a_{2}b_{2}&a_{2}b_{3}\\a_{3}b_{1}&a_{3}b_{2}&a_{3}b_{3}\\a_{4}b_{1}&a_{4}b_{2}&a_{4}b_{3}\end{bmatrix}}

або, якщо користуватись верхніми і нижніми індексами (по повторюваних індексах мається на увазі сумування):

\mathbf {a} \otimes \mathbf {b} \rightarrow a_{i}b^{j}

.

Звідси слідує, що ${\textbf {b}}\otimes {\textbf {a}}=({\textbf {a}}\otimes {\textbf {b}})^{\mathrm {T} }$ та ${\textbf {a}}({\textbf {b}}\otimes {\textbf {c}})=({\textbf {ab}})\otimes {\textbf {c}}.$

Якщо ж не прив'язуватись до матричної форми запису і матричних операцій, то, як і для тензорів більш високого рангу, прямий добуток буде являти тензор більш високого рангу (для добутку вектора-стовпця і вектора-рядка — другого, тобто з двома значками) з компонентами, які дорівнюють добутку компонент добутку множників з відповідними індексами:

P_{i}^{\ j}=a_{i}b^{j}

P_{ij}\ =a_{i}b_{j}

P^{ij}\ =a^{i}b^{j}

Оскільки тензорний добуток двох векторів є кронекеровським добутком і утворює вектор, його не слід плутати з зовнішнім добутком векторів (англ. outer product) , що називається також діадним і результатом якого є матриця (тензор другого рангу)[1][2].

Тензорним добутком простору векторів-стовпчиків на простір векторів-рядків є простір матриць.

Тензорний добуток операторів

Нехай $A:U_{1}\to U_{2}$ , $B:W_{1}\to W_{2}$ — лінійні оператори. Тензорний добуток операторів $A\otimes B:U_{1}\otimes W_{1}\to U_{2}\otimes W_{2}$ визначається за правилом

(A\otimes B)(u\otimes w)=(Au)\otimes (Bw),~~u\in U_{1},\,w\in W_{1}

Якщо матриці операторів при деякому виборі базисів мають вигляд

\mathrm {A} ={\begin{bmatrix}a_{11}&\cdots &a_{1n}\\\vdots &\ddots &\vdots \\a_{m1}&\cdots &a_{mn}\end{bmatrix}}

\mathrm {B} ={\begin{bmatrix}b_{11}&\cdots &b_{1q}\\\vdots &\ddots &\vdots \\b_{p1}&\cdots &b_{pq}\end{bmatrix}}

то матриця їх тензорного добутку запишеться в базисі, утвореному тензорним добутком базисів, у вигляді блочної матриці

\mathrm {A} \otimes \mathrm {B} ={\begin{bmatrix}a_{11}B&\cdots &a_{1n}B\\\vdots &\ddots &\vdots \\a_{m1}B&\cdots &a_{mn}B\end{bmatrix}}=

={\begin{bmatrix}a_{11}b_{11}&a_{11}b_{12}&\cdots &a_{11}b_{1q}&\cdots &\cdots &a_{1n}b_{11}&a_{1n}b_{12}&\cdots &a_{1n}b_{1q}\\a_{11}b_{21}&a_{11}b_{22}&\cdots &a_{11}b_{2q}&\cdots &\cdots &a_{1n}b_{21}&a_{1n}b_{22}&\cdots &a_{1n}b_{2q}\\\vdots &\vdots &\ddots &\vdots &&&\vdots &\vdots &\ddots &\vdots \\a_{11}b_{p1}&a_{11}b_{p2}&\cdots &a_{11}b_{pq}&\cdots &\cdots &a_{1n}b_{p1}&a_{1n}b_{p2}&\cdots &a_{1n}b_{pq}\\\vdots &\vdots &&\vdots &\ddots &&\vdots &\vdots &&\vdots \\\vdots &\vdots &&\vdots &&\ddots &\vdots &\vdots &&\vdots \\a_{m1}b_{11}&a_{m1}b_{12}&\cdots &a_{m1}b_{1q}&\cdots &\cdots &a_{mn}b_{11}&a_{mn}b_{12}&\cdots &a_{mn}b_{1q}\\a_{m1}b_{21}&a_{m1}b_{22}&\cdots &a_{m1}b_{2q}&\cdots &\cdots &a_{mn}b_{21}&a_{mn}b_{22}&\cdots &a_{mn}b_{2q}\\\vdots &\vdots &\ddots &\vdots &&&\vdots &\vdots &\ddots &\vdots \\a_{m1}b_{p1}&a_{m1}b_{p2}&\cdots &a_{m1}b_{pq}&\cdots &\cdots &a_{mn}b_{p1}&a_{mn}b_{p2}&\cdots &a_{mn}b_{pq}\end{bmatrix}}

Відповідна операція над матрицями називається добутком Кронекера, на честь Леопольда Кронекера.

Властивості

$\dim A\otimes B=\dim A\cdot \dim B$

Наступні алгебраїчні властивості засновані на канонічному ізоморфізмі:

Асоціативність

(A\otimes B)\otimes C\simeq A\otimes (B\otimes C)

Комутативність

A\otimes B\simeq B\otimes A

Лінійність

A\otimes (B\oplus C)\simeq (A\otimes B)\oplus (A\otimes C)

\oplus

— зовнішня сума лінійних просторів.

Тензорний добуток модулів над кільцем

Нехай $A_{1},A_{2},\dots ,A_{n}$ — модулі над деяким комутативним кільцем $R$ . Тензорним добутком цих модулів називається модуль $B$ над $R$ , даний разом з полілінійним відображенням $f\colon A_{1}\times \dots \times A_{n}\to B,$ що володіє властивістю універсальності, тобто такий, що для будь-якого модуля $C$ над $R$ і будь-якого полілінійного відображення $g\colon A_{1}\times \dots \times A_{n}\to C$ існує єдиний гомоморфізм модулів $h\colon B\to C$ такий, що діаграма

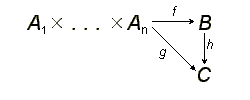
є комутативною. Тензорний добуток позначається $A_{1}\otimes \ldots \otimes A_{n}$ . Із універсальності тензорного добутку виходить, що він є визначеним з точністю до ізоморфізму.

Для доведення існування тензорного добутку будь-яких двох модулів над комутативним кільцем побудуємо вільний модуль $M$ , твірними якого будуть n-ки елементів модулів $(x_{1},\dots ,x_{n})$ де $x_{i}\in A_{i}$ . Нехай $N$ — підмодуль $M$ , що породжується такими елементами:

$(x_{1},\dots ,x_{i}+y_{i},\dots ,x_{n})-(x_{1},\dots ,x_{i},\dots ,x_{n})-(x_{1},\dots ,y_{i},\dots ,x_{n})$
$(x_{1},\dots ,\lambda x_{i},\dots ,x_{n})-\lambda (x_{1},\dots ,x_{i},\dots ,x_{n})$

Тензорний добуток визначається як фактор-модуль $B=M/N$ , клас $(x_{1},\dots ,x_{n})+N$ позначається $x_{1}\otimes \dots \otimes x_{n}$ , і називається тензорним добутком елементів $x_{i}$ , a $f$ визначається як відповідне індуковане відображення.

З 1) и 2) слідує що відображення $f\colon A_{1}\times \dots \times A_{n}\to B$ полілінійне. Доведемо, що для будь-якого модулю $C$ і будь-якого полілінійного відображення $g\colon A_{1}\times \dots \times A_{n}\to C$ існує єдиний гомоморфізм модулів $h$ , такий, що $g=h\circ f$ .

Насправді, оскільки $M$ вільний, то існує єдине відображення $h^{*}$ , що робить діаграму

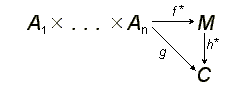
комутативною, а в силу того, що $g$ полілінійне, то на $N$ $h^{*}(N)=0$ , звідси, переходячи до індукованого відображення, отримаємо, що $h\colon M/N\to C$ , буде тим самим єдиним гомоморфізмом, існування якого і потрібно було довести.

Елементи $A_{1}\otimes \dots \otimes A_{n}$ , що представляються у вигляді $x_{1}\otimes \dots \otimes x_{n}$ , називаються розкладними.

Якщо $f_{i}\colon A_{i}\to B_{i}$ — ізоморфізми модулів, то індукований гомоморфізм, що відповідає білінійному відображенню

f_{1}\otimes \dots \otimes f_{n}\colon A_{1}\otimes \dots \otimes A_{n}\to B_{1}\otimes \dots \otimes B_{n}

що відповідає по властивості універсальності, називається тензорним добутком гомоморфізмів $f_{i}$ .

Особливо простий випадок отримується у випадку вільних модулів. Нехай $e_{i1},\dots ,e_{in}$ — базис модуля $A_{i}$ . Побудуємо вільний модуль $F$ над нашим кільцем, що має як базис елементи, які відповідають n-кам $(e_{1m},e_{2p},\dots ,e_{ns})$ , визначивши відображення $f(e_{1m},e_{2p},\dots ,e_{ns})\to (e_{1m},e_{2p},\dots ,e_{ns})$ і поширюючи його на $A_{1}\times \dots \times A_{n}$ по лінійності. Тоді $F$ є тензорним добутком, де $(e_{1m},e_{2p},\dots ,e_{ns})$ є тензорним добутком елементів $e_{1m}\otimes e_{2p}\otimes \dots \otimes e_{ns}$ . Якщо число модулів і число модулів і всі їх базиси скінченні, то

rank(A_{1}\otimes \dots \otimes A_{n})=rankA_{1}\cdot \dots \cdot rankA_{n}

.

Див. також

Примітки

Lipschutz, S.; Lipson, M. (2009). Linear Algebra. Schaum’s Outlines (вид. 4th). McGraw-Hill. ISBN 978-0-07-154352-1.
Keller, Frank (23 лютого 2020). Algebraic Properties of Matrices; Transpose; Inner and Outer Product. inf.ed.ac.uk. Процитовано 6 вересня 2020.

Література

Винберг Э. Б. Курс алгебри. — 4-е изд. — Москва : МЦНМО, 2011. — 592 с. — ISBN 978-5-94057-685-3.(рос.)

Ленг С. Алгебра. — Москва : Мир, 1968. — 564 с. — ISBN 5458320840.(рос.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Lipschutz, S.; Lipson, M. (2009). Linear Algebra. Schaum’s Outlines (вид. 4th). McGraw-Hill. ISBN 978-0-07-154352-1.

[:0-2] Keller, Frank (23 лютого 2020). Algebraic Properties of Matrices; Transpose; Inner and Outer Product. inf.ed.ac.uk. Процитовано 6 вересня 2020.