Мода (статистика)

Мо́да — значення випадкової величини, що трапляється найчастіше в сукупності спостережень. Це таке значення x, в якому функція мас ймовірностей набуває максимального значення. Іноді трапляється більше аніж одна мода (наприклад: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 і 9). У такому випадку можна сказати, що сукупність мультимодальна. Із структурних середніх величин лише мода має таку унікальну властивість. Як правило мультимодальність вказує на те, що набір даних не підпорядковується нормальному розподілу.

Мода, як середня величина, вживається частіше для даних, що мають нечислову природу. Серед перелічених кольорів автомобілів — «білий», «чорний», «синій металік», «білий», «синій металік», «білий» — мода дорівнюватиме значенню «білий». За експертної оцінки з її допомогою визначають найпопулярніші типи продукту, що враховується при прогнозі продажів чи плануванні їх виробництва.

Іншими словами, мода є найпоширеніше значення випадкової величини (ознаки). У дискретному ряду вона визначається візуально за найбільшою частотою (часткою), а в інтервальному — таким чином визначається модальний інтервал, а конкретне модальне значення розраховується за формулою:

Mo={x_{0}+h{\frac {f_{mo}-f_{mo-1}}{(f_{mo}-f_{mo-1})+(f_{mo}-f_{mo+1})}}};

де

х₀ та h — нижня межа та ширина модального інтервалу,
f_mo, f_mo-1, f_mo+1 — частоти (частки) відповідно модального, передмодального та післямодального інтервалів.

Мода вибірки

Мода вибірки це такий елемент, що з'являється в наборі найчастіше. Наприклад, модою вибірки [1, 3, 6, 6, 6, 6, 7, 7, 12, 12, 17] є 6. В наступному наборі даних [1, 1, 2, 4, 4] мода не є унікальною – такий набір даних називають бімодальним, а набір із більше ніж однією модою - мультимодальним.

Для вибірки для неперервного розподілу, такої як [0.935..., 1.211..., 2.430..., 3.668..., 3.874...], це поняття в своїй початковій формі є непридатним, оскільки не існує двох точно однакових значень вибірки, оскільки кожне значення буде зустрічатися точно один раз. Для того, щоб визначити моду в даному випадку, типовою практикою є дискретизація даних, після якої значення частоти виникнення призначається інтервалам із однаковим розміром, оскільки це робиться при побудові гістограм, призначаючи цьому інтервалу значення його середньої точки. Мода як правилом є тим значенням де гістограма досягає свого максимуму. Для малих і середніх за розміром вибірок результат цієї процедури дуже чутливий до обраної величини інтервалу, якщо він може бути обраним занадто вузьким чи занадто широким; зазвичай інтервал обирають так, щоб значна частка даних була сконцентрована у відносно не великій кількість інтервалів (від 5 до 10), так, щоб частка даних що випадає за межі цих інтервалів також була значною. Альтернативним підходом може бути ядрова оцінка густини розподілу, який розмиває точки вибірки таким чином, аби утворити неперервну оцінку функції густини імовірностей, яка забезпечує можливість оцінки моди.

Наступний код для програмного застосунку MATLAB (або Octave) розраховує моду вибірки:

X = sort(x);
indices   =  find(diff([X; realmax]) > 0); % індекси, де повторювані значення змінюються
[modeL,i] =  max (diff([0; indices]));     % найдовша довжина серії повторюваних значень
mode      =  X(indices(i));

На першому кроці алгоритм потребує відсортувати вибірку в порядку зростання. Потім він розраховує дискретну похідну відсортованого спису, аби знайти індекси де ця похідна є доданою. Потім він розраховує дискретну похідну цього отриманого набору індексів, знаходить максимум цієї похідної індексів, і зрештою отримує значення із відсортованої вибірки у цій точці максимуму, що відповідатиме останньому входженню послідовності повторюваних значень.

Порівняння середнього, медіани і моди

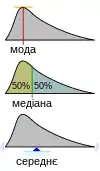
Геометрична візуалізація моди, медіани і середнього значення довільної функції густини імовірностей.[1]

Порівняння різних загальних середніх значень на прикладі вибірки вибірки { 1, 2, 2, 3, 4, 7, 9 }
Тип	Опис	Приклад	Результат
Середнє арифметичне	Сума всіх значень вибірки поділена на кількість цих елементів вибірки: $\scriptstyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}$	(1+2+2+3+4+7+9) / 7	4
Медіана	Середнє значення, що відокремлює більшу половину і меншу половину вибірки	1, 2, 2, 3, 4, 7, 9	3
Мода	Значення, що зустрічається у вибірці найчастіше	1, 2, 2, 3, 4, 7, 9	2

Застосування

На відміну від середнього і медіани, поняття моди має сенс навіть для випадку із "номінальними даними" (тобто таких, що не складаються із числових значень, що необхідно для середнього, або навіть можуть не бути впорядкованими значеннями як для випадку із медіаною). Наприклад, якщо мова йде про вибірку популярності корейських імен, можна встановити, що ім'я "Кім" зустрічається частіше ніж будь-яке інше. В такому випадку "Кім" буде модою даною вибірки. При проведенні будь-якої процедури голосування, де множина голосів означає перемогу, визначити переможця можна у випадку існування одного значення моди, а якщо результат буде мультимодальним зазвичай проводять другий тур голосування, або застосовують якусь додаткову процедуру визначення переможця.

На відміну від медіани, поняття моди має сенс для будь-які випадкової величини що може приймати значення із векторного простору, включаючи дійсні числа (одно-вимірний векторний простір) і цілі числа (які можна вважати вбудованими в дійсні). Наприклад, для розподілу точок на площині зазвичай можна отримати середнє і моду, а концепцію медіани тут застосувати не можна. Медіана матиме сенс якщо існує лінійне впорядкування можливих значень.

Властивості

За умови визначеності, і для спрощення унікальності, наведемо наступні її найбільш важливі властивості.

Всі три міри мають таку властивість: Якщо над випадковою величиною (або кожним значенням вибірки) виконують лінійне або афінне перетворення, що заміняє величину X на aX+b, то те саме перетворення відбудеться із середнім, медіаною і модою.
Крім випадку дуже малих вибірок, мода є чутливою до "викидів" (такі як випадкові, не часті, хибні експериментальні вимірювання). Медіана більш стійка до присутності викидів, в той час як середнє також чутливе до них.
Для неперервних одномодальних розподілів медіана часто знаходиться між середнім і модою, близько на третій частині відстані між середнім і модою. У вигляді формули, медіана ≈ (2 × середнє + мода)/3. Це правило Карла Пірсона, часто застосовується для злегка не симетричних розподілів, які за формою подібні до нормального розподілу, але це правило не завжди буде вірним в загальному випадку і ці три статистичні міри можуть бути в довільному порядку.[2][3]
Для одномодальних розподілів, мода знаходиться в межах ${\sqrt {3}}$ стандартних відхилень від середнього, а корінь із сереньоквадратичного відхилення від моди знаходиться між значеннями одного стандартного відхилення і двох стандартних відхилень.[4]

Приклад із не симетричними розподілами

Прикладом не симетричного розподілу є розподіл особистого достатку людей: Декілька людей є дуже багатими, але серед них є деякі, які є екстремально багатими. Однак, досить велика кількість є бідними.

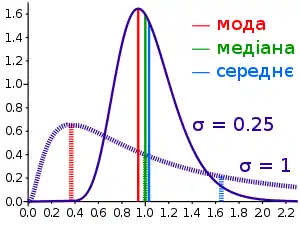
Порівняння середнього, медіани і моди двох логнормальних розподілів із різними коефіцієнтами асиметрії.

Добре відомий клас розподілів, які можуть мати довільну асиметрію це логнормальний розподіл. Він отримується шляхом перетворення випадкової величини X, що має нормальний розподіл у випадкову величину Y = e^X. Тоді логарифм випадкової величини Y є нормально розподіленим, з чого і була утворена назва розподілу.

Якщо прийняти, що μ величини X дорівнює 0, медіана величини Y буде дорівнювати 1, не залежно від стандартного відхилення σ величини X. Це тому що X має симетричний розподіл, так що його медіана також дорівнює 0. Перетворення величини X у Y є монотонним, тому медіана e⁰ = 1 для Y.

Коли X має стандартне відхилення σ = 0.25, розподіл Y є злегка асиметричним. Використавши формули для логнормального розподілу, отримаємо:

{\begin{array}{rlll}{\text{середнє}}&=e^{\mu +\sigma ^{2}/2}&=e^{0+0.25^{2}/2}&\approx 1.032\\{\text{мода}}&=e^{\mu -\sigma ^{2}}&=e^{0-0.25^{2}}&\approx 0.939\\{\text{медіана}}&=e^{\mu }&=e^{0}&=1\end{array}}

Насправді, медіана знаходиться приблизно на третині відстані від середнього до моди.

Коли X має більше стандартне відхилення, σ = 1, розподіл Y буде сильно асиметричним. Тепер

{\begin{array}{rlll}{\text{середнє}}&=e^{\mu +\sigma ^{2}/2}&=e^{0+1^{2}/2}&\approx 1.649\\{\text{мода}}&=e^{\mu -\sigma ^{2}}&=e^{0-1^{2}}&\approx 0.368\\{\text{медіана}}&=e^{\mu }&=e^{0}&=1\end{array}}

Тут, правило Пірсона не виконується.

Нерівність Ван Звета

Ван Звет отримав нерівність, що має достатні умови, за яких вона є правдивою.[5] Нерівність

Мода ≤ Медіана ≤ Середнє

виконується коли

F( Медіана - x ) + F( Медіана + x ) ≥ 1

для всіх x де F() - кумулятивна функція розподілу імовірностей.

Див. також

Примітки

AP Statistics Review - Density Curves and the Normal Distributions. Процитовано 16 березня 2015.
Relationship between the mean, median, mode, and standard deviation in a unimodal distribution.
Hippel, Paul T. von (2005). Mean, Median, and Skew: Correcting a Textbook Rule. Journal of Statistics Education 13 (2). doi:10.1080/10691898.2005.11910556.
Bottomley H. Maximum distance between the mode and the mean of a unimodal distribution. — 2004.
van Zwet, WR (1979). Mean, median, mode II. Statistica Neerlandica 33 (1): 1–5. doi:10.1111/j.1467-9574.1979.tb00657.x.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] AP Statistics Review - Density Curves and the Normal Distributions. Процитовано 16 березня 2015.

[2] Relationship between the mean, median, mode, and standard deviation in a unimodal distribution.

[3] Hippel, Paul T. von (2005). Mean, Median, and Skew: Correcting a Textbook Rule. Journal of Statistics Education 13 (2). doi:10.1080/10691898.2005.11910556.

[4] Bottomley H. Maximum distance between the mode and the mean of a unimodal distribution. — 2004.

[vanZwet1979-5] van Zwet, WR (1979). Mean, median, mode II. Statistica Neerlandica 33 (1): 1–5. doi:10.1111/j.1467-9574.1979.tb00657.x.