Логнормальний розподіл
Логнорма́льний розпо́діл у теорії ймовірностей — двопараметричне сімейство абсолютно неперервних розподілів. Якщо випадкова величина має логнормальний розподіл, то її логарифм має нормальний розподіл.
| Логнормальний | |
|---|---|
 Деякі щільності лог-нормального розподілу з однаковими параметрами локалізації μ, але різними параметрами масштабу σ | |
|
Функція розподілу ймовірностей 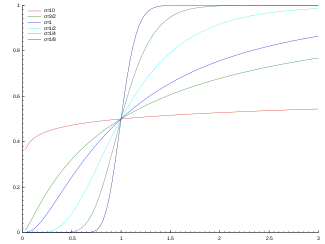 Функція розподілу лог-нормального розподілу (з μ = 0 ) | |
| Параметри |
σ2 > 0 — форма (дійсне), μ ∈ R — логарифмічний-масштаб |
| Носій функції | x ∈ (0, +∞) |
| Розподіл імовірностей | |
| Функція розподілу ймовірностей (cdf) | |
| Середнє | |
| Медіана | |
| Мода | |
| Дисперсія | |
| Коефіцієнт асиметрії | |
| Коефіцієнт ексцесу | |
| Ентропія | |
| Твірна функція моментів (mgf) | (визначена тільки на від'ємній півосі) |
| Характеристична функція | представлення є асимптотично розбіжне, але достатньо точне для числового використання |
Визначення
Нехай розподіл випадкової величини задається щільністю ймовірності, що має вид:
- ,
де . Тоді кажуть, що має логнормальний розподіл з параметрами і . Пишуть: .
Властивості логнормального розподілу
.
Зв'язок з іншими розподілами
- Якщо , то
- .
Моделювання логнормальних випадкових величин
Для моделювання звичайно використовується зв'язок з нормальним розподілом. Тому, достатньо згенерувати нормально розподілену випадкову величину, наприклад, використовуючи перетворення Бокса-Мюллера, і обчислити її експоненту.
Моделювання
Моделювання значень випадкової величини з логнормальним розподілом (з параметрами і ) проводиться за формулою , де має нормальний розподіл з тими ж параметрами.
Застосування логнормального розподілу
У статистиці так званий логнормальний розподіл застосовується в тому випадку, коли починає змінюватися ціна активу в майбутньому, а це — випадковий процес, що в принципі повинний описуватися нормальним розподілом. Водночас для цілей імовірнісної оцінки вартості активу в теорії використовують не нормальний, а логнормальний розподіл. Це обумовлено наступним:
- По-перше, нормальний розподіл симетричний щодо її центральної осі і може мати як додатні, так і від'ємні значення; однак ціна активу не може бути від'ємною.
- По-друге, нормальний розподіл говорить про рівну імовірність для відхилення значень змінної чи нагору вниз. У той же час на практиці, наприклад, має місце інфляція, що натискає на ціни убік їхнього підвищення, а також сама тимчасова сутність грошей: вартість грошей сьогодні менше, ніж вартість грошей учора, але більше, ніж вартість грошей завтра.
Крива логнормального розподілу завжди додатня і має правобічну скошеність (асиметрично), тобто вона вказує на велику імовірність відхилення ціни вгору. Тому якщо, допустимо, ціна активу становить 50 дол., то крива логнормального розподілу свідчить про те, що пут-опціон з ціною виконання 45 дол. повинний коштувати менше колл-опціону із ціною виконання 55 дол., у той час як відповідно до нормального розподілу вони повинні були б мати однакову ціну. Хоча не можна сподіватися, що приведені вихідні припущення в точності виконуються у всіх реальних ринкових ситуаціях, проте прийнято вважати, що логнормальний розподіл є достатньо добрим як перше наближення у випадку активів, якими торгують на конкурентних ринках аукціонного типу для довгих розглянутих періодів.
