Невизначений інтеграл

• в задачах про обчислення швидкості або прискорення руху тіла;
• в задачах про обчислення визначених інтегралів (див. формулу Ньютона-Лейбніца);
• при розв'язанні диференціальних рівнянь.

Невизначеним інтегралом від функції f(x)=2x є сукупність її первісних x²+C, де C — довільна стала

Функція f називається підінтегральною функцією, f(x)dx — підінтегральним виразом, C  — сталою інтегрування, x — змінною інтегрування.

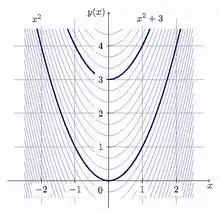
З геометричної точки зору невизначений інтеграл — це сукупність (сім'я) ліній F(x) + C (див. Рис.).

З означень первісної та невизначеного інтеграла випливають наступні властивості (за умов існування первісних та похідних на інтервалі J):

${\displaystyle 1.\ {\frac {d}{dx}}\int f(x)\,dx=f(x),\quad x\in J;}$

${\displaystyle 2.\ \int f'(x)\,dx=f(x)+C,\quad x\in J;}$

${\displaystyle 3.\ \forall \,\alpha \in \mathbb {R} ,\ \alpha \neq 0:\quad \int \alpha f(x)\,dx=\alpha \int f(x)dx,\quad x\in J;}$

${\displaystyle 4.\ \int (f_{1}(x)+f_{2}(x))\,dx=\int f_{1}(x)\,dx+\int f_{2}(x)\,dx,\quad x\in J.}$

Для обчислення невизначених інтегралів використовуються

• Таблиця основних формул інтегрування
• Метод підстановки (або формула заміни змінної)
• Метод інтегрування частинами

За допомогою згаданих методів можна знаходити невизначені інтеграли у вигляді скінченних комбінацій елементарних функцій. Проте не всі інтеграли можна виразити через елементарні функції. Відомо небагато класів функцій, інтегрування яких в результаті дає елементарні функції. До цих класів відносяться раціональні, тригонометричні, показникові функції та функції з радикалами.

Якщо ж інтеграл не можна виразити скінченною комбінацією елементарних функцій, тоді його розглядають як нову функцію (яка є інтегралом Рімана зі змінною верхнею межею інтегрування) і обчислюють за допомогою рядів або нескінченних добутків елементарних функцій.[1]

Так, наприклад, інтеграли

${\displaystyle \int {\frac {1}{\ln x}}\,dx,\qquad \int e^{x^{2}}\,dx}$

існують, проте через елементарні функції не виражаються.

• Невизначений інтеграл функції комплексної змінної
• Первісна
• Інтегральне числення
  • Визначений інтеграл
    • Інтеграл Рімана
    • Інтеграл Стілтьєса (або інтеграл Рімана—Стілтьєса)
    • Інтеграл Лебега
    • Інтеграл Даніелла
    • Інтеграл Бохнера
  • Відомі інтеграли

• Дороговцев А. Я. Математический анализ. — К. : Факт, 2004. — 560с.
• Фихтенгольц Г. М. Основы математического анализа в 2 т. / Под ред. Головиной Л. И. — Москва : Наука, 196. — 1968. — Т. 1.

• Невизначений інтеграл // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 368. — 594 с.