Первісна

Пе́рві́сною для функції f(x) називається така функція F(x), похідна якої F'(x) дорівнює f(x).

Первісними для функції f(x)=2x є функції вигляду x²+C, де C — довільна стала

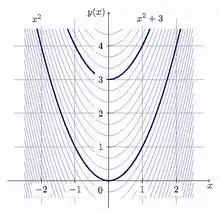
Операція взяття первісної є оберненою (в деякому сенсі) до операції взяття похідної: первісними для похідної f(x) будуть функції F(x) + C, де C ∈ R — довільна стала (зокрема, однією з первісних буде сама функція F(x)). І навпаки, похідною від первісної F(x) для функції f(x) буде сама функція f(x).

Формальне означення та властивості первісної

Надалі через J будемо позначати довільний непорожній інтервал дійсних чисел (відкритий або замкнений, обмежений або необмежений).

Означення. Функція F(x) називається первісною (примітивною) для функції f(x) на інтервалі J дійсної осі, якщо f(x) = F'(x) для всіх x ∈ J.

Нехай функція F — первісна функції f на інтервалі J. Тоді

функція F(x) є неперервною на інтервалі J;
функція F(x) + C теж є первісною для f на J, де C ∈ R — довільна стала (якщо функція f(x) має первісну, то вона має нескінченну кількість первісних);
будь-яка первісна для f на J може бути представлена у вигляді F(x) + C, де C ∈ R — довільна стала.

Приклад. Для функції y = 3x² первісними є функції F(x) = x³, F(x) = x³ + 5, F(x) = x³ − 6 тощо (на довільному інтервалі J).

Не всі функції мають первісну.

Приклад. Функція

f(x)=\mathop {\mathrm {sign} } \,x={\begin{cases}-1,&x<0,\\0,&x=0,\\1,&x>0,\end{cases}}

не має первісної на відрізку [−1, 1].[1]

Теорема. Для довільної неперервної на деякому інтервалі J функції f існує первісна на цьому інтервалі.[2]

Методи знаходження первісної

Знаходження первісної для заданої функції f(x) називається інтегруванням. Для обчислення первісної використовуються ті самі методи, що і для обчислення невизначеного інтегралу, а саме

Не завжди первісну можна записати у вигляді скінченної комбінації елементарних функцій (наприклад, функція exp(x²) має первісну як неперервна функція, проте ця первісна не виражається аналітично). В такому разі первісну треба шукати у вигляді функціонального ряду або нескінченного добутку елементарних функцій.

Див. також

Примітки

Доведення див. в § 5.1.1 в Дороговцев А. Я. Математический анализ. — К. : Факт, 2004. — 560с.
Доведення див. в п. 183 Фихтенгольц Г. М. Основы математического анализа в 2 т. / Под ред. Головиной Л. И. — Москва : Наука, 196. — 1968. — Т. 1.

Джерела

Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Москва : Наука, 1962. — Т. 1. — 607 с.(рос.)
Іваненко, О. О. Курс лекцій з математичного аналізу [Текст : навч. посіб. / О. О. Іваненко, Т. В. Іваненко. — Суми : СумДУ, 2011. — 534 с.]
Динамічні математичні моделі FIZMA.neT

Посилання

Первісна функція // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 368. — 594 с.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Доведення див. в § 5.1.1 в Дороговцев А. Я. Математический анализ. — К. : Факт, 2004. — 560с.

[2] Доведення див. в п. 183 Фихтенгольц Г. М. Основы математического анализа в 2 т. / Под ред. Головиной Л. И. — Москва : Наука, 196. — 1968. — Т. 1.