Інтеграл Рімана

Інтегра́л Рі́мана — одне з найважливіших понять математичного аналізу, є узагальненням поняття суми, яке знаходить широке застосування в багатьох галузях математики. Був уведений Бернгардом Ріманом в 1854 році, і є однією з перших формалізацій поняття інтегралу.

Інтеграл Рімана функції f(x) по відрізку [a, b] дорівнює сумі площ фігур між графіком функції f(x), віссю Ox і прямими {x=a} та {x=b}, в якій доданки, що відповідають фігурам в нижній півплощині, беруться зі знаком «−»

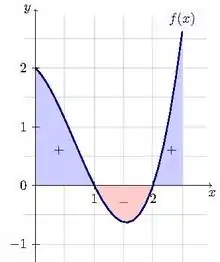
Геометрична інтерпретація

Ріман формалізував поняття інтегралу, розроблене Ньютоном та Лейбніцем, як площу фігури, яка обмежена графіком функції та віссю абсцис. Для цього він розглянув ступінчасті фігури, які складаються з великої кількості вертикальних прямокутників, отриманих при розбитті відрізка інтегрування.

Нехай функція f : [a, b]→R є неперервною і невід'ємною на відрізку [a, b]. Фігура, обмежена графіком цієї функції, відрізком [a, b] і прямими {x = a} та {x = b}, називається криволінійною трапецією. Обчислимо наближено площу цієї трапеції.

Розіб'ємо відрізок [a, b] на n відрізків (n ≥ 1): a = x₀ < x₁ < x₂ < … < x_k < x_k+1 < … < x_n−1 < x_n = b. Множина точок {x₀, x₁,…, x_n} називається розбиттям відрізку інтегрування і позначається як λ або λ([a, b]).
На кожному відрізку розбиття [x_k, x_k+1] довільно оберемо по одній точці c_k (k = 0, 1,…, n − 1) і побудуємо вертикальні прямокутники Π_k = [x_k, x_k+1] × [0, f(c_k)].
Смугу криволінійної трапеції з основою [x_k, x_k+1] замінимо прямокутником Π_k.

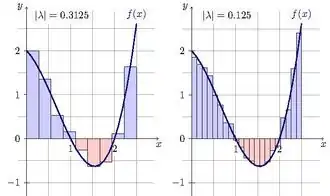
В результаті отримаємо ступінчасту фігуру, складену з прямокутників.

Очевидно, що чим менші відрізки [x_k, x_k+1] розбиття, тим більше ступінчаста фігура наближається до криволінійної трапеції.

Зауваження. Якщо для розбиття λ довжини усіх відрізків однакові (тобто Δx_k := x_k+1 − x_k = Δx =: (b − a) / n для всіх k = 0,…, n − 1), то таке розбиття називається рівномірним.

Означення. Діаметром (розміром, дрібністю) розбиття λ = {x₀, x₁,…, x_n} називається число |λ| = max {Δx_k, 0 ≤ k ≤ n − 1}.

Означення. Величина

S(f,\,\lambda ,\,\{c_{i}|\lambda \})=\sum _{k=1}^{n}f(c_{k})\Delta x_{k},

називається інтегральною сумою для функції f та точок {c_i | λ}, які відповідають розбиттю λ.

Інтегральна сума дорівнює площі ступінчастої фігури, і її природно вважати наближеним значенням площі криволінійної трапеції. А за площу криволінійної трапеції природно прийняти границю чисел S(f, λ, {c_i | λ}), коли |λ| → 0:

S=\lim _{|\lambda |\rightarrow 0}S(f,\,\lambda ,\,\{c_{i}|\lambda \})=\lim _{|\lambda |\rightarrow 0}\sum _{k=1}^{n}f(c_{k})\Delta x_{k}.

До обчислення границь такого типу приводять багато задач, наприклад, обчислення довжини пройденого шляху при прямолінійному русі за відомою швидкістю v(t) протягом часу від моменту t₁ до t₂.

Означення інтеграла Рімана

Чим дрібніший діаметр розбиття λ, тим ближче значення інтегральної суми до значення інтеграла Рімана

Означення (інтеграла Рімана). Нехай функція f : [a, b] → R (a < b) та

для довільного розбиття λ відрізка [a, b] та відповідного йому набору точок {c_i | λ} існує скінченна границя інтегральних сум S(f, λ, {c_i | λ}) при |λ| → 0,
границя інтегральних сум S(f, λ, {c_i | λ}) не залежить від розбиття λ і вибору точок c_i.

Тоді таку границю називають інтегралом Рімана функції f по відрізку [a, b] і позначають символом

\int _{a}^{b}f(x)\,dx.

У цьому випадку функція f(x) називається інтегровною (за Ріманом) на [a, b]; в протилежному випадку f(x) є неінтегровною (за Ріманом) на відрізку [a, b].

Термінологія. Функція f називається підінтегральною функцією, f(x)dx — підінтегральним виразом, x — змінною інтегрування, числа a та b — нижньою та верхньою межами інтегрування відповідно.

Позначення. Множину інтегровних за Ріманом функцій на відрізку [a, b] позначають R([a, b]).

Необхідною умовою інтегровності функції за Ріманом є її обмеженість: якщо функція f(x) необмежена на відрізку [a, b], то границя інтегральних сум для цієї функції буде рівна ∞.

Властивості інтеграла Рімана

Властивості, пов'язані з проміжками інтегрування

Орієнтовність інтеграла: має місце поняття інтеграла Рімана по відрізку «в зворотньому напрямку», а саме для a > b вважаємо, що

\int _{a}^{b}f(x)\,dx:=-\int _{b}^{a}f(x)\,dx;

Інтеграл по відрізку нульової довжини: має місце поняття інтеграла Рімана по відрізку нульової довжини, а саме для довільного a ∈ R вважаємо, що

\int _{a}^{a}f(x)\,dx:=0;

Інтегровність на меншому відрізку: якщо f ∈ R([a, b]), то f ∈ R([c, d]) для довільного відрізку [c, d] ⊂ [a, b];

Адитивність: якщо f ∈ R([a, b]) ∩ R([b, c]) (a < b < c), то f ∈ R([a, c]) і

\int _{a}^{c}f(x)\,dx=\int _{a}^{b}f(x)\,dx+\int _{b}^{c}f(x)\,dx;

Властивості зі знаком рівності

В цьому підрозділі вважаємо, що {a, b} ⊂ R — довільні.

Невиродженість: для всіх {a, b} ⊂ R має місце рівність

\int _{a}^{b}1\,dx=b-a;

Лінійність: якщо {f, g} ⊂ R([a, b]), то для довільних {α, β} ⊂ R([a, b]) функція αf + βg ∈ R([a, b]) та

\int _{a}^{b}(\alpha f(x)+\beta g(x))\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx.

Граничний перехід під знаком інтеграла Рімана: якщо f_i ∈ R([a, b]) рівномірно збігаються на [a, b] до функції f, то f ∈ R([a, b]) та

\lim _{i\to \infty }\int _{a}^{b}f_{i}(x)\,dx=\int _{a}^{b}f(x)\,dx

Нерівності

В цьому підрозділі вважаємо, що a < b.

Невід'ємність: якщо f ∈ R([a, b]) та невід'ємна на [a, b], то

\int _{a}^{b}f(x)\,dx\geq 0;

Нерівність інтегралів: якщо {f, g} ⊂ R([a, b]) та f(x) ≤ g(x) для всіх x ∈ [a, b], то

\int _{a}^{b}f(x)\,dx\leq \int _{a}^{b}g(x)\,dx;

Оцінка модуля інтеграла: якщо f ∈ R([a, b]), то |f| ∈ R([a, b]) та

\left|\int _{a}^{b}f(x)\,dx\right|\leq \int _{a}^{b}|f(x)|\,dx.

Інтегровність за Ріманом функцій

В цьому розділі наведено твердження, які дозволяють визначити, чи є функція інтегровна за Ріманом.

Критерій Дарбу інтегровності функції

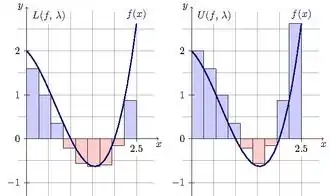
Суми Дарбу для рівномірного розбиття λ: нижня (зліва) та верхня (справа)

Нижня та верхня суми Дарбу́ для функції f(x) та розбиття λ — це інтегральні суми, в яких відповідні точки {c_i | λ} обираються як точні нижня та верхня межі функції f(x) відповідно.

Означення. Інтегральна сума для розбиття λ, для якої відповідні точки {c_i | λ} вибираються з умови c_i = inf_{[x_i, x_i+1]} f(x), називається нижньою сумою Дарбу для функції f та розбиття λ і позначається одним із символів L(f, λ) (від англ. lower — «нижній») або s(f, λ).

Означення. Інтегральна сума для розбиття λ, для якої відповідні точки {c_i | λ} вибираються з умови c_i = sup_{[x_i, x_i+1]} f(x), називається верхньою сумою Дарбу для функції f та розбиття λ і позначається одним із символів U(f, λ) (від англ. upper — «верхній») або S(f, λ).

За допомогою верхньої та нижньої сум Дарбу можна дати критерій інтегровності функції за Ріманом.

Теорема. Нехай f : [a, b] → R — обмежена функція. Функція f ∈ R([a, b]) тоді і лише тоді, коли

\lim _{|\lambda |\to 0}(S(f,\,\lambda )-s(f,\,\lambda ))=0.

Класи інтегровних за Ріманом функцій

Теорема (про інтегровність неперервної функції). C([a, b]) ⊂ R([a, b]), тобто кожна неперервна на відрізку [a, b] функція є інтегровною за Ріманом на цьому відрізку.

Теорема (про інтегровність монотонної функції). Кожна монотонна на відрізку [a, b] функція є інтегровною за Ріманом на цьому відрізку.

Теорема (про інтегровність функції зі скінченною кількістю точок розриву). Нехай f : [a, b] → R задовольняє умовам

функція f(x) обмежена на [a, b];
f ∈ C([a, b] \ {z₁, z₂,…, z_n}).

Тоді f ∈ R([a, b]).

Приклад (неінтегровної обмеженої функції). Покажемо, що функція Діріхле

D(x):={\begin{cases}1,&x\in \mathbb {Q} \\0,&x\in \mathbb {R} \setminus \mathbb {Q} \end{cases}}

не інтегровна на довільному відрізку [a, b] ⊂ R. Тут Q — це множина раціональних чисел, а R — множина дійсних чисел.

На довільному відрізку [α, β] ⊂ R знайдуться як раціональна, так і ірраціональна точки. Тому при довільному розбитті λ відрізка [a, b] маємо

s(f,\,\lambda )=0,\qquad S(f,\,\lambda )=b-a,

звідки у відповідності з критерієм Дарбу інтегровності функції D ∉ R([a, b]).

Методи обчислення інтегралів Рімана

Теорема. Припустимо, що функція f задовольняє умовам

f ∈ R([a, b]);
f має первісну F на [a, b].

Тоді справедлива формула Ньютона—Лейбніца:

\int _{a}^{b}f(x)\,dx=F(x){\Bigr |}_{x=a}^{b}:=F(b)-F(a),

З формулою Ньютона—Лейбніца обчислення інтеграла Рімана зводиться до знаходження первісної для підінтегральної функції (див. методи знаходження первісної). Проте нею слід користуватися обережно, спочатку переконавшись у тому, чи задовільняє підінтегральна функція обом умовам теореми.

Приклад. Розглянемо інтеграл $\int _{-1}^{1}{\frac {dx}{x^{2}}}.$ «Первісна» підінтегральної функції дорівнює F(x) = −1/x. Тоді згідно з формулою Ньютона—Лейбніца шуканий інтеграл дорівнює F(1) − F(−1) = −2 < 0, що суперечить властивості невід'ємності інтеграла Рімана, оскільки f(x) = 1/x² > 0.

У наведеному «обчисленні» інтеграла допущено дві помилки:

даний інтеграл не існує, оскільки підінтегральна функція необмежена на відрізку [-1, 1];
функція f(x) розривна в точці x = 0, яка належить відрізку інтегрування, тому вона не має первісної на цьому відрізку.

Обчислення інтеграла Рімана за означенням

Безпосереднє обчислення визначеного інтеграла, виходячи з його означення (як границя інтегральних сум) зазвичай досить громіздке, однак все ж таки можливе.

Приклад. Обчислимо інтеграл

\int _{a}^{b}\sin x\,dx.

Покладемо f(x) = sin x, x ∈ [a, b]. Оскільки f ∈ C([a, b]), то f ∈ R([a, b]), тому для обчислення інтегралу досить знайти границю довільної послідовності інтегральних сум. Розглянемо рівномірне розбиття λ_n відрізку [a, b] на n рівних частин, Δx = (b − a) / n, і запишемо інтегральну суму

{\begin{aligned}S(f,\,\lambda _{n},\,\{c_{i}|\lambda _{n}\})&=\Delta x\sum _{k=1}^{n}\sin(a+k\Delta x)=\\&={\frac {\Delta x}{2\sin {\frac {\Delta x}{2}}}}\sum _{k=1}^{n}2\sin(a+k\Delta x)\sin {\frac {\Delta x}{2}}=\\&={\frac {\Delta x}{2\sin {\frac {\Delta x}{2}}}}\sum _{k=1}^{n}{\Big (}\cos(a+k\Delta x-{\frac {1}{2}}\Delta x)-\cos(a+kh+{\frac {1}{2}}\Delta x){\Big )}=\\&={\frac {\Delta x}{2\sin {\frac {\Delta x}{2}}}}{\Big (}\cos(a+{\frac {1}{2}}\Delta x)-\cos(b+{\frac {1}{2}}\Delta x){\Big )}.\end{aligned}}

Спрямувавши |λ_n| до нуля, отримаємо, що

{\begin{aligned}\int _{a}^{b}\sin x\,dx&=\lim _{\Delta x\to 0}{\frac {\Delta x}{2\sin {\frac {\Delta x}{2}}}}{\Big (}\cos(a+{\frac {1}{2}}\Delta x)-\cos(b+{\frac {1}{2}}\Delta x){\Big )}=\\&=\cos b-\cos a.\end{aligned}}

Приклад. Обчислимо інтеграл

\int _{0}^{1}e^{x}\,dx.

Покладемо f(x) = e^x, x ∈ [0, 1]. Оскільки f ∈ C([0, 1]), то f ∈ R([a, b]). Отже, у відповідності з критерієм Дарбу інтегровності функцій

\int _{0}^{1}f(x)\,dx=\lim _{|\lambda _{n}|\rightarrow 0}s(f;\lambda _{n}),

де λ_n — рівномірне розбиття відрізка [0, 1] на n рівних частин. Отже, маємо

{\begin{aligned}s(f;\,\lambda _{n})&=\sum _{i=0}^{n-1}e^{\frac {i}{n}}\cdot {\frac {1}{n}}=\\&={\frac {e-1}{e^{\frac {1}{n}}-1}}\cdot {\frac {1}{n}},\end{aligned}}

звідки випливає, що

{\begin{aligned}\int _{0}^{1}f(x)\,dx&=\lim _{n\rightarrow \infty }{\frac {e-1}{e^{\frac {1}{n}}-1}}\cdot {\frac {1}{n}}=\\&=e-1.\end{aligned}}

Інтеграл Рімана як функція верхньої межі інтегрування

Означення

Припустимо, що f ∈ R([a, b]) (отже, f ∈ R([a, x]) для довільного x ∈ [a, b]). Покладемо

\varphi (x):=\int _{a}^{x}f(u)\,du,\quad x\in [a,b].

Вочевидь, φ(а) = 0.

Властивості

Якщо f ∈ R([a, b]), то φ ∈ С([a, b]).

Якщо f ∈ C([a, b]), то φ ∈ С¹([a, b]), причому для довільного x ∈ [a, b]: φ'(x) = f(x).

Якщо f ∈ C([a, b]), то f має первісну на [a, b]. Первісними для f на [a, b] будуть функції вигляду φ(x) + c, c ∈ ℝ.

Формула Лейбніца

Теорема. Нехай

f : ℝ → ℝ інтегровна за Ріманом по кожному відрізку;
f має первісну на ℝ;
функції a, b : ℝ → ℝ диференційовні на ℝ.

Тоді

{\frac {d}{dx}}\int _{a(x)}^{b(x)}f(u)\,du=f(b(x))b'(x)-f(a(x))a'(x),\quad x\in \mathbb {R} .

Історія

Таке означення інтеграла дано Коші[1], але воно застосовувалося лише до неперервних функцій.

Ріман в 1854 році[2], дав це ж означення без припущення неперервності.

Див. також

Посилання

Cauchy A. L., Sur la mécanique céleste et sur un nouveau calcul appelé calcul des limites, Turin 1831
Riemann В., «Göttinger Akad. Abhandl.», 1868, Bd 13

Література

Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Москва : Наука, 1964. — Т. 2. — 800 с.(рос.)
Зорич В. А. Математический анализ. — 10-е. — М : МЦНМО, 2019. — Т. 1. — 564 с. — ISBN 978-5-4439-4029-8.(рос.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Cauchy A. L., Sur la mécanique céleste et sur un nouveau calcul appelé calcul des limites, Turin 1831

[2] Riemann В., «Göttinger Akad. Abhandl.», 1868, Bd 13