Опорна пряма

В геометрії, пряма L є опорною прямою до кривої C в площині, якщо вона містить точку C, але не розділяє будь-які дві точки C[1]. Іншими словами, C повністю лежить в одній з двох замкнених півплощин, на які ділить площину пряма L, і має хоча б одну точку на L.

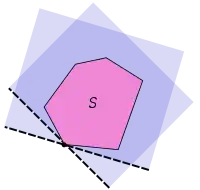
Дві опорні прямі до кривої, яка обмежує S

Буває через точку кривої проходить багато опорних прямих (див. малюнок). Коли в заданій точці існує дотична пряма, тоді, якщо вона не перетинає криву, дотична і буде опорною прямою в цій точці, притому єдиною.

Поняття опорної прямої також має сенс для плоских фігур. У цьому випадку кажуть, що опорна пряма може бути визначена як пряма, що має спільні точки з границею фігури, але не з її внутрішньою частиною.[2]

Якщо дві обмежені зв'язні плоскі фігури мають опуклі оболонки, які не перетинаються, тобто їх відділяє додатня відстань, то вони обов'язково мають точно чотири загальні опорні прямі, дотичні в двох різних точках двох опуклих оболонок. Дві з цих опорних прямих розділяють фігури по різним півплощинам, і називаються критичними опорними прямими.[2]

Властивості опуклих фігур
  • До кожної обмеженої опуклої фігури можна провести лише дві опорні прямі, паралельні заданому напряму[3]
  • Через кожну точку опуклої кривої можна провести хоча б одну опорну пряму[3][4]
  • Якщо через кожну граничну точку фігури проходить хоча б одна опорна пряма, то фігура є опуклою[3][4]
  • Найбільша відстань між паралельними опорними прямими опуклої фігури є діаметром цієї фігури[3]

Узагальнення

У випадку більших вимірностей опорна пряма узагальнюється на опорну гіперплощину.

Локальна опорність
В кожній точці є локальна опорна пряма, але не в кожній точці вона буде глобально опорною

Криву C називають локально опорною на пряму L в точці , якщо існує такий окіл U точки x, для якого L — опорна пряма.

Локально опукла крива завжди має локально опорну пряму. Наявність локально опорної прямої не гарантує локальної опуклості кривої.

Якщо в точці кривої існує локально опорна пряма, то кривина кривої в цій точці буде невід'ємною.

Опорність на іншу криву

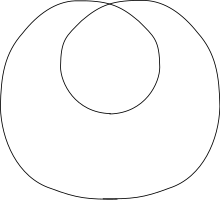
Замість опорності на пряму можна розглядати опорність на іншу криву. Наприклад, на коло.

Опорність кривої в точці на коло радіусу R означає, що кривина кривої в цій точці буде не менше .


Посилання
  1. «The geometry of geodesics», Herbert Busemann, p. 158
  2. «Encyclopedia of Distances», by Michel M. Deza, Elena Deza, p. 179
  3. «Выпуклые фигуры», И. М. Яглом и В. Г. Болтянский[недоступне посилання з липня 2019], C. 19-25
  4. О. А. Борисенко, Л. М. Ушакова. Аналітична геометрія: Навч. посібник для студ. мат. спец. ун-тів. — Харків : Основа, 1993. — С. 59-60.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.