Осциляції Фріделя
Осциляції Фріделя[1] — періодичний розподіл електронної густини, що виникає при екрануванні електричного заряду дефекту.[2] Названі на честь французького фізика Жака Фріделя. Виникають внаслідок локалізованих збурень у металевій або напівпровідниковій системі, викликаних дефектом у фермі-газі або фермі-рідині.[3]
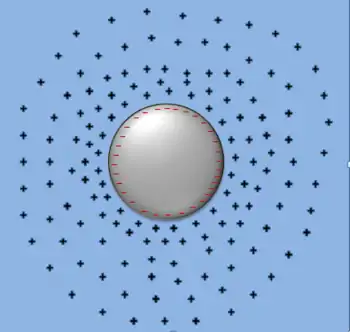
Осциляції Фріделя є квантово-механічним аналогом екранування електричного заряду заряджених частинок у «басейні» іонів (див. Рис. 1). У той час, як екранування електричного заряду використовує поняття точкових зарядів для опису складу іонного "басейну", осциляції Фріделя, що описують ферміони в фермі-рідині або фермі-газі, вимагають квантового опису розсіювання електронних хвиль на потенціалі дефекту. Такі осциляції відображують характерний експоненціальне загасання ферміонної щільності поблизу збурення, за яким слідує загасання з осциляціями (r - відстань від дефекту).
Розсіювання на дефекті
Електрони, що рухаються в металі або напівпровіднику, подібні вільним електронам з хвильовою функцією у вигляді плоскої хвилі, тобто
- .
Електрони в металі поводяться інакше, ніж частинки у звичайному газі, оскільки електрони є ферміонами, і вони підкоряються статистиці Фермі-Дірака. Така поведінка означає, що кожен k - стан у газі може бути зайнятий лише двома електронами з протилежним спіном. Зайняті стани заповнюють сферу в зонній структурі k - простору до фіксованого енергетичного рівня — енергії Фермі . Радіус кулі в k - просторі, , називається хвильовим вектором Фермі, — ефективна маса.
Якщо в металі або напівпровіднику знаходиться чужорідний атом, так звана домішка, електрони, які вільно рухаються у провіднику, розсіюються потенціалом домішки. Оскільки електронний газ є фермі-газом, лише електрони з енергіями, близькими до рівня Фермі, можуть брати участь у процесі розсіювання, тому що повинні існувати порожні кінцеві стани з близькою енергією, в які могли б перейти розсіяні електрони. Стани навколо рівня Фермі, які можуть бути розсіяні, займають обмежений діапазон k — значень або довжин хвиль. Тому лише електрони в обмеженому діапазоні довжин хвиль поблизу енергії Фермі розсіюються, що призводить до модуляції густини заряду навколо домішки. Для сферично симетричного потенціалу домішки, що має позитивний заряд, у тривимірному металі густина заряду осцилює, як функція відстані від домішки :
- ,
де — орбітальне квантове число, — фаза розсіювання парціальної компоненти хвильової функції електрона, - діелектрична проникність металу з хвильовим вектором, що дорівнює подвоєний вектор Фермі. Надлишкова кількість електронів навколо домішкового йона визначається правилом сум Фріделя:
Для довільної розмірності електронної системи, , доданок до густини заряду на великій відстані від дефекту має вигляд:[4]
Якісний опис
У класичному сценарії екранування електричного заряду спостерігається загасання електричного поля в зарядженій рідині, при наявності зарядженого об'єкта. Оскільки екранування електричного заряду розглядає рухомі заряди в рідині як точкові об'єкти, концентрація цих зарядів відносно відстані від точки зменшується експоненціально. Це явище описується рівнянням Пуассона–Больцмана.[5]
Локалізований біля дефекту заряд створюється швидкими електронами фермі-газу, які притягуються до дефекту, дещо сповільнюють свій рух біля нього та скупчуються в цій області. Існування різкої границі довжин електронних хвиль призводить до виникнення ефектів квантової інтерференції, в наслідок чого навколо центу, що розсіює, виникає гало заряду.[6]
Примітка. Там, де класично поблизу зарядженого збурення можна спостерігати переважну кількість протилежно заряджених частинок, у квантовомеханічному сценарії осциляцій Фріделя — це періодичні розташування протилежно заряджених ферміонів, за якими слідують простори з такими ж зарядженими областями.[3]
Візуалізація двовимірних осциляцій

Сканувальна тунельна мікроскопія дозволяє з атомною роздільністю досліджувати локальну густину електронних станів (ЛГС) поблизу поверхні провідника:
де — хвильова функція електрона з урахуванням розсіювання на дефекті, — енергія електрона з двовимірним хвильовим вектором , — дельта-функція Дірака. Розсіювання на дефекті призводить до інтерференції хвиль і зміни густини станів, що відображає розсіювальні властивості дефекту.[8] Типовими дефектами поверхні є адсорбовані чужорідні одиничні атоми (точкові дефекти) і атомарні сходинки (лінійні дефекти) (Рис.2). Одним зі способів розуміння якісних характеристик стоячих хвиль біля східчастого краю є наближення, в котрому плоский східчастий край моделюється непроникним бар'єром для електронів поверхневих станів. Східчастий край створює вузол ЛГС, , на межі сходинки , а ЛГС на відстані від сходинки описується рівнянням:[8]
,
де — функція Бесселя першого роду.

На Рис. 3 — двовимірні осциляції Фріделя проілюстровано СТМ - зображенням чистої поверхні заліза на якій розміщені наноостровки кобальту. На зображенні добре видно двовимірні фріделівські осциляції густини електронних станів біля точкових дефектів та меж острівків.
Посилання
- http://gravityandlevity.wordpress.com/2009/06/02/friedel-oscillations-wherein-we-learn-that-the-electron-has-a-size/ - просте пояснення цього явища
Примітки
- W. A. Harrison (1979). Solid State Theory. Dover Publications. ISBN 978-0-486-63948-2.
- Фриделя осцилляции. Энциклопедия физики и техники.
- Friedel Oscillations: wherein we learn that the electron has a size. Gravity and Levity. 2 червня 2009. Процитовано 22 грудня 2009.
- Kai Sotthewes, Michiel Nijmeijer, and Harold J. W. Zandvliet Confined Friedel oscillations on Au(111) terraces probed by thermovoltage scanning tunneling microscopy. PHYSICAL REVIEW B 103, 245311 (2021)
- Hans-Jürgen Butt, Karlheinz Graf, and Michael Kappl, Physics and Chemistry of Interfaces, Wiley-VCH, Weinheim, 2003.
- 'Принципы теории твердого тела'; Займан, Дж.; Изд-во: М.: Мир, 1966
- «Atomic-scale Observations of Alloying at the Cr-Fe(001) Interface» by A. Davies, J.A. Stroscio, D.T. Pierce, and R.J. Celotta, Phys. Rev. Lett. 76, 4175 (1996).
- M. F. Crommie, C. P. Lutz, and D. M. Eigler, Nature (London) 363, 524 (1993); Science 262, 218 (1993).
- Spin mapping at the nanoscale and atomic scale. Roland Wiesendanger. Rev. Mod. Phys. 81, 1495 (2009)