Енергія Фермі
Енергія Фермі — енергія найвищого заповненого одночастинкового стану в системі ферміонів при температурі абсолютного нуля.
Необхідно відзначити, що термін «енергія Фермі» досить часто помилково вживається в значенні «хімічний потенціал».[1] Значення хімічного потенціалу для системи ферміонів збігається з енергією Фермі тільки при температурі абсолютного нуля, проте відрізняються при вищих температурах.
Вступ
Основна концепція
При застосуванні квантової механіки до багаточастинкових систем популярна модель, в якій квантовий стан складної системи утворюється зі станів окремих частинок — одночастнинкове наближення (дивіться, наприклад, одноелектронне наближення). При цьому взаємодією між частинками нехтують, або вважають її врахованою при визначенні одночастинкових станів у наближенні середнього поля. У межах цієї моделі група часток або квазічасток, знана як ферміони (наприклад, електрони, протони та нейтрони є ферміони) підпорядковується принципу Паулі, який стверджує, що в одному квантовому стані можуть перебувати тільки ферміони з різним значенням спіну. Таких ферміонів 2S+1, де S — спінове квантове число, у випадку частинок зі спіном 1/2 кількість ферміонів в одному стані — 2.
Кожний одночастинковий стан позначається набором квантових чисел. У системі, що містить багато ферміонів (подібно до електронів у металах), кожний ферміон буде мати різний набір квантових чисел. Для визначення найнижчої енергії системи ферміонів, спершу необхідно згрупувати стани в набори з однаковою енергією та впорядкувати їх за зростанням енергії. Потім, розпочинаючи з порожньої системи, шляхом додавання часток, послідовно наповнюють незаповнені квантові стани з найменшими енергіями. Вичерпавши всі частки, отримують енергію найвищого заповненого стану і буде називатися енергією Фермі.
Це означає, що навіть якщо забрати всю можливу енергію з металу шляхом охолодження до абсолютного нуля температур (0 Кельвінів), електрони в металі все одно будуть рухатися далі; при чому найшвидші з них будуть мати швидкості, які відповідають кінетичній енергії, рівній енергії Фермі. Це і є швидкості Фермі. Енергія Фермі є однією з найважливіших концепцій у фізиці конденсованого стану. Вона використовується, наприклад, при опису металів, діелектриків та напівпровідників. Вона також відіграє ключову роль у фізиці надпровідників, у фізиці квантових рідин при температурах рідкого гелію (в обох випадках — нормальних та надплинних рідинах 3He). Вона також важлива в ядерній фізиці, в астрономії під час розгляду стабільності білих карликів в умовах гравітаційного колапсу.
Додаткові відомості
Енергія Фермі (EF) системи невзаємодіючих ферміонів збільшує значення своєї енергії основного стану, коли навіть один електрон додається до системи. Вона може бути інтерпретована, як максимальна енергія індивідуального ферміона, що перебуває в основному стані. Хімічний потенціал при температурі абсолютного нуля рівний енергії Фермі.
Модельні системи
Приклад використання концепції до одновимірної квадратної ями
Одновимірна прямокутна яма нескінченної глибини — квантова модель для одновимірного потенціального ящика. Це одна із найпростіших задач квантової механіки, і тому її розв'язок для однієї частки відомий. Рівні енергії тут позначаються квантовими числами n, а енергії для ями з шириною дорівнюють:
- .
Припустимо, що замість однієї частки в потенціальному ящику, ми маємо N часток, і ці частки є ферміонами зі спіном 1/2. Тоді тільки дві частки можуть мати однакову енергію, тобто дві частки можуть мати енергію , дві частки можуть мати енергію і так далі. Причина, що дві частки можуть мати однакову енергію, полягає в тому, що частки з напівцілим спіном можуть мати спін 1/2 (спін вгору) або спін −1/2 (спін вниз), що приводить до формування двох станів для кожного рівня енергії. Щодо повної енергії системи, то вона є найнижчою (основний стан) при такій конфігурації, коли всі енергетичні рівні аж до n=N/2 є заповнені, а всі вищі рівні енергії — порожні. Тому енергія Фермі є:
- .
Таким чином, значення енергії Фермі залежить від кількості частинок у системі. Цей висновок справедливий і для інших систем.
Тривимірний випадок
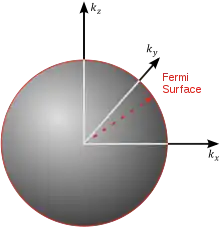
У тривимірному ізотропний випадку заповнені стани утворюють в оберненому просторі так звану сферу Фермі.
Розглянемо тривимірний кубічний ящик, котрий має ребро довжини L (див. Квантовий рух у прямокутній потенційній ямі). Цей підхід є доброю апроксимацією для опису електронів у металах, коли закон дисперсії електронних станів у валентній зоні металів близький до параболічного. Стани в цьому випадку позначаються квантовими числами nx, ny, and nz. Енергія однієї частки тут буде:
де nx, ny, nz — додатні цілі числа. Тут ми маємо вироджені стани із однаковою енергією . Тепер можна заповнити цей ящик невзаємодіючими ферміонами (N штук) зі спіном 1/2. Щоб обчислити енергію Фермі, припустимо що N дуже велике.
Якщо ввести вектор , тоді кожний квантовий стан відповідає певній точці в 'n-просторі' з енергією Фермі:
Число станів з енергією меншою ніж Ef, дорівнює числу станів, котрі лежать всередині сфери радіуса в області n-простору, де nx, ny, nz є додатні цілі числа. В основному стані загальна кількість таких чисел із врахуванням проекцій спіна дорівнює числу ферміонів у системі.
тут «двійка» враховує наявність двох спінових станів; коефіцієнт 1/8 враховує те, що тільки 1/8 частина сфери лежить в області, де всі n додатні.
Знаходимо:
тому енергія Фермі буде:
- ,
яке можна переписати у вигляді співвідношення між енергією Фермі та числом часток на одиницю об"єму (при заміні L2 на V2/3):
Повна енергія сфери Фермі при наявності ферміонів буде:
Повна енергія Фермі:
Інтегрування шляхом заміни змінних дає:
Перехід від до дає:
Похідні терміни
Рівень Фермі є найвищий рівень заповнений рівень енергії при абсолютному нулі, так що всі нижні рівні енергії — зайняті електронами, а всі верхні рівні енергії порожні. Оскільки ферміони не можуть співіснувати при ідентичних енергіях (див. Принцип Паулі), при абсолютному нулі температур, тому електрони упаковуються на станах із найнижчою енергією і формують т.з. «море Фермі» електронних енергетичних станів.
У випадку параболічного закону дисперсії у цьому стані (при 0 K), середня енергія електрона задається виразом:
де — енергія Фермі.
Імпульс Фермі — імпульс ферміона на поверхні Фермі. Імпульс Фермі задається виразом:
де — ефективна маса електрона.
Швидкість Фермі — це швидкість ферміонів на поверхні Фермі. Вона визначається як:
- ,
Поняття імпульсу Фермі і швидкості Фермі використовується у випадку дисперсійних співвідношень між енергією та імпульсом, що не залежать від напряму. В загальнішому випадку ці величини визначені неоднозначно, тому необхідно обмежитися використанням поняття «енергії Фермі».
Можна також ввести поняття температури Фермі, що враховує квантові ефекти при охолодженні. Температура Фермі визначається як:
де k — константа Больцмана.
Тверде тіло
Енергія Фермі твердотільних систем залежить від структури одноелектронних енергетичних рівнів у цих системах, у випадку кристалів — від зонної структури. У випадку напівпровідників та діелектриків в основному стані цих кристалів валентна зона повністю заповнена, тому енергія Фермі збігається з верхом валентної зони. В напівпровідниках із акцепторами енергія Фермі збігається з акцепторним рівнем. Для багатьох металів, валентна зона яких заповнена не повністю, справедлива описана вище модель сфери Фермі. Для інших металів, і особливо напівметалів розрахунок енергії Фермі вимагає точного знання зонної структури. У цьому випадку поверхня Фермі дуже далека від сферичної.
Білі карлики
Зорі, знані як білі карлики, мають масу, співмірну з масою нашого Сонця, проте їхній радіус майже в 100 разів менше. Висока густина означає, що електрони вже не є зв'язані з одиничними ядрами, а формують вироджений електронний газ. Густина електронів у білих карликах складає величину порядка 1036 м−3. А це означає, що енергія Фермі тут буде:
- еВ.
Ядра
Іншим типовим прикладом використання концепції є частки в ядрі атома. Радіус ядра можна грубо оцінити як:
- де A — число нуклонів.
Тому густина нуклонів в ядрі буде:
- м−3
Оскільки енергія Фермі прикладається тільки для нуклонів одного типу, тому її необхідно зменшити вдвічі. Це тому, що присутність нейтронів не впливає на енергію Фермі протонів в ядрі, і навпаки.
Тому енергія Фермі для ядра наближено:
- 30 × 106 еВ = 30 МеВ
Радіус ядра дозволяє відхилення від вказаного значення, тому типові значення енергії Фермі — близько 38 МеВ.
Заповнені і незаповнені орбіталі
В рамках квантової механіки ферміони — частки з напівцілим спіном, як правило 1/2, такі як електрони, що підкоряються принципу Паулі, тому на кожному енергетичному рівні може знаходитися тільки два електрони. Очевидно, що ферміони підкоряються статистиці Фермі — Дірака. Основний стан невзаємодіючих ферміонів системи формується шляхом поступового заповнення порожніх енергетичних рівнів аж до рівня Фермі. Коли найвищий енергетичний рівень буде заповнений (рівень Фермі), тоді енергія Фермі є енергією найвищої заповненої молекулярної орбіталі (НЗМО). У випадку провідних матеріалів це значення збігається із значенням енергії найнижчих незаповнених орбіталей (ННМО). Проте структура енергетичних рівнів більшості матеріалів (діелектриків і напівпровідників) така, що між ННМО та НЗМО існує проміжок енергії, заборонена зона, в якому нема енергетичних станів. Цей проміжок може мати ширину до 5-6 еВ.
Вільний електронний газ
У вільному електронному газі, квантовомеханічній версії ідеального газу, квантові стани можуть бути позначені за їхніми імпульсами. Аналогічно, для періодичної системи, такої як електронний газ у періодичній кристалічній ґратці металу, можна ввести поняття квазі-імпульс (див. хвилі Блоха). В будь-якому випадку, енергія Фермі розміщується у просторі імпульсів на поверхні, яку називають поверхнею Фермі. Для вільного електронного газу поверхня Фермі має вигляд сфери; для періодичної системи, вона має загалом складну форму (див. зони Брілюена). Об'єм оберненого простору під поверхнею Фермі визначає число електронів у системі, а топологія поверхні Фермі визначає транспортні властивості металів, такі як електрична провідність. Дисципліна, що вивчає поверхню Фермі часто називають ферміологією. Поверхні Фермі більшості металів добре досліджені, як на теоретичному, так і на практичному рівнях.
При параболічному законі дисперсії хімічний потенціал вільного газу електронів пов'язаний з енергією Фермі співвідношенням:
де EF — енергія Фермі, k — константа Больцмана.а T — температура. Звідси випливає, що хімічний потенціал приблизно дорівнює енргії Фермі при температурах, значно менших від характеристичної температури Фермі EF/k. Характеристична температура є величина порядка 105 K для металів, тому при кімнатних температурах (300 K) енергія Фермі та хімічний потенціал приблизно однакові. Це важливо, оскільки саме хімічний потенціал, а не енергія Фермі, використовується в статистиці Фермі-Дірака.
Різниця між значенням хімічного потенціалу і енергією Фермі визначає ступінь виродження електронного газу. У випадку, коли ці значення близькі, наприклад, для металів, електронний газ вироджений, тобто суттєво квантовий, у випадку, коли вони далекі (), наприклад, у власних і слаболегованих напівпровідниках, електронний газ невироджений, тобто близький за своїми властивостями до класичного.
Література
- Використання терміну «енергія Фермі» для хімічного потенціалу — поширене явище в численних монографіях та статтях з фізики напівпровідників. Так, наприклад, Жак Панков (Pankove), в Optical Processes in Semiconductors, ISBN 0-486-60275-3 (1971), стверджує: "Рівень Фермі є енергія, при якій ймовірність її заповнення електронами, дорівнює 0,5. (ст. 6)
- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
- Table of fermi energies, velocities, and temperatures for various elements.
- a discussion of fermi gases and fermi temperatures.
