Паралелогон

Паралелогон — багатокутник, що замощує простір з використанням лише паралельного перенесення, при цьому сторони паралелогонів суміщуються за цілими сторонами[1].

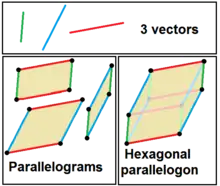
Паралелогон побудований як дві або три пари паралельних відрізків. Вершини і ребра всередині шестикутника видаляються
Існує п'ять решіток Браве в двовимірному просторі, пов'язані з замощеннями паралелогонами і їх п'ятьма варіантами симетрії

Паралелогон повинен мати парне число сторін і протилежні сторони мають бути рівні за довжиною і паралельні (згідно з назвою). Менш очевидне обмеження — паралелогон може мати лише чотири або шість сторін[1]. Чотиристоронній паралелогон є паралелограмом. У загальному випадку паралелогон має обертову симетрію на 180 градусів відносно центру.

Два типи

Чотирикутні і шестикутні паралелогони мають різні форми геометричної симетрії. В загальному випадку вони мають центральну симетрію з порядком 2. Шестикутні паралелогони можуть бути неопуклими.

Число
сторін		 Приклади Назва Симетрія
і її порядок
4 Паралелограм Z2, порядок 2
Прямокутник і ромб Dih2, 4 порядок
Квадрат Dih4, порядок 8
6 Подовжений
паралелограм		 Z2, порядок 2
Подовжений
ромб		 Dih2, 4 порядок
Правильний
шестикутник		 Dih6, 12 порядок

Геометричні варіанти

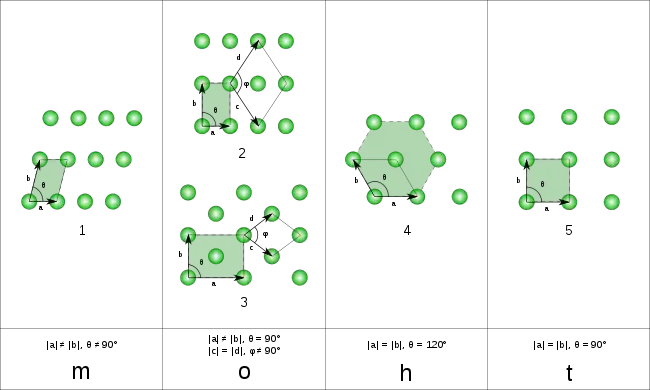
Паралелограми можуть замостити площину як деформована квадратна мозаїка, тоді як шестикутні паралелогони можуть замостити площину як деформована правильна шестикутна мозаїка.

Мозаїка з паралелограмів
1 довжина 2 довжини
Прямий Косий Прямий Косий
Квадрат
p4m (*442)		 Ромб
cmm (2*22)		 Прямокутник
pmm (*2222)		 Паралелограм
p2 (2222)
Мозаїка з шестикутних паралелогонів
1 довжина 2 довжини 3 довжини
Правильний шестикутник
p6m (*632)		 Подовжений ромб
cmm (2*22)		 Подовжений паралелограм
p2 (2222)

Див. також
  • Паралелоедр — узагальнення паралелогона в тривимірному просторі

Примітки
  1. Александров, 1950, с. 323.

Література
  • А.Д. Александров. Выпуклые многогранники. — Москва, Ленинград : Государственное издательство технико-теоретической литературы, 1950.
  • Catherine A. Gorini. The Facts on File Geometry Handbook. — New York : Facts On File, Inc, 2003. — С. 117. — ISBN 0-8160-4875-4.
  • B. Grünbaum, G.C. Shephard. list of 107 isohedral tilings // Tilings and Patterns. — New York : W. H. Freeman & Co, 1987. — С. 473-481. — ISBN 0-7167-1193-1.
  • Fedorov's Five Parallelohedra
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.