Проєктивна границя

Проєктивна границя (обернена границя) — конструкція, що використовується в різних розділах математики яка дозволяє побудувати новий об'єкт $X$ через множину однотипних об'єктів $X_{i},$ які є проіндексовані деякою напрямленою множиною і набору відображень $f_{ij}:X_{j}\to X_{i}$ , $i\leqslant j$ . Проєктивні границі є одним із видів границі в теорії категорій. Для проєктивної границі зазвичай використовуються наступні позначення:

X=\varprojlim X_{i}

,

X=\projlim X_{i}

.

Проєктивну границю можна визначити в довільній категорії. Двоїсте поняття — індуктивна границя.

Означення

Алгебричні структури

Для алгебричних систем можна дати відносно просте означення проєктивної границі. Нехай $I$ — частково впорядкована множина $\leqslant$ (наприклад, множина цілих чисел) і для кожного елемента $i\in I$ задана деяка алгебрична система $X_{i}$ з будь-якого фіксованого класу (наприклад, абелевих груп, модулів над заданим кільцем), а кожній парі $(i,\;j)$ , такій що $i,\;j\in I$ , $i\leqslant j$ — гомоморфізм $f_{ij}:X_{j}\to X_{i}$ , причому $f_{ii}$ — тотожні відображення для будь-якого $i\in I$ і $f_{ik}=f_{ij}\circ f_{jk}$ для будь-яких $i\leqslant j\leqslant k$ з $I$ . Тоді проєктивна границя $X$ є за означенням підсистемою прямого добутку $X_{i}$ виду:

\varprojlim X_{i}={\bigg \{}(x_{i})\in \prod _{i\in I}X_{i}\mid x_{i}=f_{ij}(x_{j})\forall i\leqslant j{\bigg \}}

.

Існують канонічні проєкції $\pi _{i}:X\to X_{i}$ , які вибирають $i$ -у компоненту прямого добутку для кожного $i\in I$ . Ці проєкції повинні бути гомоморфізмами, виходячи з цього можна ввести додаткову алгебричну структуру на проєктивній границі.

Загальний випадок

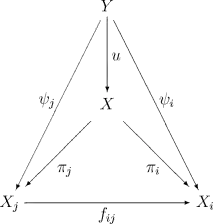
У довільній категорії проєктивну границю можна описати за допомогою її універсальної властивості. Нехай $(X_{i},f_{ij})$ — сімейство об'єктів і морфізмів категорії C, яке задовольняє тим же вимогам, що і в попередньому пункті. Тоді $X$ називається проєктивною границею системи $(X_{i},f_{ij})$ , або $X=\varprojlim X_{i}$ , якщо виконані наступні умови:

Існує таке сімейство відображень $\pi _{i}:X\to X_{i}$ , що $\pi _{i}=f_{ij}\circ \pi _{j}$ для будь-яких $i\leqslant j$ ;
Для будь-якого сімейства відображень $\psi _{i}:Y\to X_{i}$ , довільної множини $Y$ , для якої виконані рівності $\psi _{i}=f_{ij}\circ \psi _{j}$ для будь-яких $i\leqslant j$ , існує єдине відображення $u:Y\to X$ , для якого $\psi _{i}=\pi _{i}\circ u$ , для всіх $i\in I$ .

Більш загально, проєктивна границя — границя в категорному сенсі системи $(X_{i},f_{ij})$ .

Приклади

Цілі $p$ -адичні числа є проєктивною границею послідовності $\mathbb {Z} _{p^{n}}$ з природними відображеннями виду отримання залишку $\mathbb {Z} _{p^{n}}\to \mathbb {Z} _{p^{m}}$ при $n\geqslant m$ .
Кільце $\textstyle R[[t]]$ формальних степеневих рядів над комутативним кільцем $R$ є проєктивною границею кілець $\textstyle R[t]/t^{n}R[t]$ , індексованих натуральними числами, з природними проєкціями $\textstyle R[t]/t^{n+j}R[t]\to \textstyle R[t]/t^{n}R[t]$ .
Множина Кантора є гомеоморфною проєктивній границі добутків двоточкових множин (з дискретною топологією) з проєкціями на перші кілька координат як відображень.
В категорії топологічних просторів проєктивні границі задаються ініціальною топологією на відповідній множині-носії.

Див. також

Література

Bourbaki, Nicolas (1989). Algebra I. Springer. ISBN 978-3-540-64243-5. OCLC 40551484.
Bourbaki, Nicolas (1989). General topology: Chapters 1-4. Springer. ISBN 978-3-540-64241-1. OCLC 40551485.
Mac Lane, Saunders (September 1998). Categories for the Working Mathematician (вид. 2nd). Springer. ISBN 0-387-98403-8.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.