Проєктивний об'єкт

Об'єкт ${\displaystyle P}$ у категорії ${\displaystyle {\mathcal {C}}}$ називається проєктивним якщо для довільного епіморфізма ${\displaystyle e:E\twoheadrightarrow X}$ і морфізма ${\displaystyle f:P\to X}$, існує морфізм ${\displaystyle {\overline {f}}:P\to E}$ для якого ${\displaystyle e\circ {\overline {f}}=f}$, тобто існує комутативна діаграма:

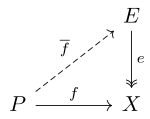
У локально малій категорії ${\displaystyle {\mathcal {C}}}$ ${\displaystyle P}$ є проєктивним якщо і тільки якщо функтор Hom

${\displaystyle \operatorname {Hom} (P,-)\colon {\mathcal {C}}\to \mathbf {Set} }$

зберігає епіморфізми.[1]

• Кодобуток двох проєктивних об'єктів є проєктивним об'єктом.[2]
• Ретракт проєктивного об'єкта є проєктивним.[3]

Нехай ${\displaystyle {\mathcal {A}}}$ — абелева категорія. Кажуть, що ${\displaystyle {\mathcal {A}}}$ має достатньо проєктивних об'єктів якщо для кожного об'єкта ${\displaystyle A}$ у ${\displaystyle {\mathcal {A}}}$ існує проєктивний об'єкт ${\displaystyle P}$ у ${\displaystyle {\mathcal {A}}}$ і точна послідовність

${\displaystyle P\longrightarrow \longrightarrow 0.}$

Іншими словами ${\displaystyle p\colon P\to A}$ є епіморфізмом.

• Твердження про те, що всі множини є проєктивними об'єктами є еквівалентним аксіомі вибору.
• Проєктивний об'єктами у категорії абелевих груп є вільні абелеві групи.
• Нехай ${\displaystyle R}$ — кільце з 1. Розглянемо (абелеву) категорію лівих ${\displaystyle R}$-модулів ${\displaystyle {\mathcal {M}}_{R}}$. Проєктивними об'єктами у ${\displaystyle {\mathcal {M}}_{R}}$ є проєктивні ліві R-модулі. Зокрема ${\displaystyle R}$ є проєктивним об'єктом у ${\displaystyle {\mathcal {M}}_{R}.}$
• Категорія лівих (правих) ${\displaystyle R}$-модулів має достатньо проєктивних об'єктів. Це випливає з того, що для кожного лівого (правого) ${\displaystyle R}$-модуля ${\displaystyle M}$, можна взяти вільний (а відтак проєктивний) ${\displaystyle R}$-модуль ${\displaystyle F}$ породжений елементами ${\displaystyle M}$ і канонічна проєкція ${\displaystyle \pi \colon F\to M}$ буде необхідним сюр'єктивним відображенням.

• Ін'єктивний об'єкт
• Проєктивний модуль