Рівноприскорений рух
Рівноприскорений рух — найпростіший вид механічного руху, при якому прискорення залишається сталим. Частковим випадком рівноприскореного руху є рівносповільнений рух, який відбувається тоді, коли напрямки початкової швидкості і прискорення протилежні.[1]
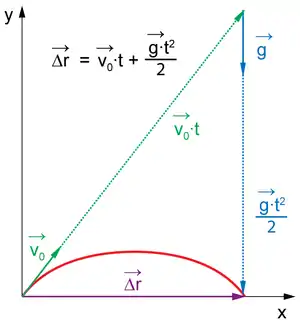
Прикладом такого руху є політ в однорідному полі сили тяжіння каменя, кинутого під кутом до горизонту за умови, що опором повітря можна знехтувати: камінь летить зі сталим прискоренням , спрямованим вертикально вниз.
Траєкторія має вигляд ділянки параболи або прямої.
Загальна формула:
- ,
де — прискорення (визначається в SI в м/с2), — кінцева швидкість, — початкова швидкість, — час.
Формули швидкості та шляху для прискореного руху:
1) при одновимірному рівноприскореному русі швидкість тіла змінюється з часом лінійно за законом:
- ;
2) формула координати тіла:
- ;
3) формула проєкції переміщення:
- ;
4) формула проєкції переміщення, якщо невідомий:
Характер рівноприскореного руху
Рівноприскорений рух відбувається в площині, що містить вектори прискорення і початкової швидкості . З урахуванням того, що (тут — радіус-вектор), траєкторію описує вираз
- .
На заданому інтервалі часу вона являє собою ділянку параболи, яка за паралельності (тобто спів- або проти-спрямованості) векторів і перетворюється на відрізок прямої.
Для кожної з координат, скажімо , можна записати вирази аналогічної структури:
- ,
де — складова прискорення вздовж осі , а — радіус-вектор матеріальної точки в момент (, , — орти).
У прикладі з каменем , компоненти прискорення , , початкова швидкість , , , при цьому , а отже, .
Переміщення і швидкість
У разі рівноприскореного руху будь-яка з компонент швидкості, наприклад , залежить від часу лінійно:
- .
При цьому зв'язок між переміщенням () вздовж координати і швидкістю вздовж тієї ж координати такий:
- .
Звідси можна отримати вираз для - складової кінцевої швидкості тіла за відомих -складових початкової швидкості і прискорення:
- .
Якщо , то , а .
Вирази для зміщень , і компонент швидкості вздовж координат і набувають такого ж вигляду, як для і , але символ усюди слід замінити на або .
У підсумку, за теоремою Піфагора, модуль переміщення буде
- ,
а модуль кінцевої швидкості знайдемо як
- .
Рівноприскорений рух не може відбуватися необмежено довго: це означало б, що, починаючи з якогось моменту часу , модуль швидкості тіла перевищить величину швидкості світла у вакуумі , що виключено теорією відносності.
Умова здійснення
Рівноприскорений рух реалізується, коли на тіло (матеріальну точку) діє стала сила , зазвичай в однорідному гравітаційному або електростатичному полі, якщо величина швидкості тіла значно менша, ніж швидкість світла . Тоді, за другим законом Ньютона, прискорення буде
де через — маса тіла. У прикладі з каменем роль відіграє сила тяжіння.
Якщо ж швидкість тіла порівнянна зі швидкістю світла, то закон Ньютона в наведеному вигляді непридатний. При цьому, в разі дії сталої сили, відбувається так званий релятивістський рівноприскорений рух, за якого сталим є тільки власне прискорення, а прискорення у фіксованій інерційній системі відліку наближається з часом до нуля в міру наближення величини швидкості до її межі .
Теорема про кінетичну енергію точки
Формула переміщення при рівноприскореному русі використовується для доведення теореми про кінетичну енергію. Для цього слід перенести прискорення в ліву частину і домножити обидві частини на масу тіла:
- .
Записавши аналогічні співвідношення для координат і і підсумувавши всі три рівності, отримаємо співвідношення:
- .
Зліва стоїть робота сталої рівнодійної сили , а праворуч — різниця кінетичних енергій у кінцевий і початковий моменти руху. Отримана формула являє собою математичний вираз теореми про кінетичну енергію точки для випадку рівноприскореного руху[2].
Рівнозмінний рух
Рівнозмінним називають рух, за якого тангенціальна (паралельна швидкості) складова прискорення стала[3]. Такий рух не є рівноприскореним, крім ситуації, коли він відбувається вздовж прямої, але в математичному плані його можна розглянути аналогічно.
У цьому випадку вводиться узагальнена координата , яку часто називають шляхом, що відповідає довжині пройденої траєкторії (довжині дуги кривої). Таким чином, формула набуває вигляду:
- ,
де — тангенціальне прискорення, яке «відповідає» за зміну модуля швидкості тіла. Для швидкості маємо:
- .
При маємо рух зі сталою за модулем швидкістю.
Іноді прикметник рівнозмінний замінюють на криволінійний равноприскорений, що вносить плутанину, оскільки, скажімо, рівноприскорений рух каменя по кривій (параболе) в поле тяжіння не рівнозмінний.
Див. також
- Релятивістський рівноприскорений рух
Примітки
- Física 4ª (іспанська). Мексика: CECSA. 2004. ISBN 970-24-0257-3.
- Тарг С. М. Краткий курс теоретической механики. — 11-е изд. — М. : «Высшая школа», 1995. — С. 214. — ISBN 5-06-003117-9.
- Див. Физический энциклопедический словарь — М.: Советская энциклопедия, под. ред. А. М. Прохорова (1983), стаття «Равнопеременное движение», стор. 602.
