Теорема де Брейна — Ердеша (теорія графів)

Хроматичне число нескінченного графу, якщо це число скінченне, дорівнює найбільшому хроматичному числу серед усіх його скінченних підграфів.

• Еквівалентне формулювання: будь-який k-критичний граф скінченний.
• Теорема застосовується для розширення задачі чотирьох фарб і теореми Ділуорса для скінченних графів і множин із частковим порядком до нескінченних варіантів, зведення задачі Нельсона — Ердеша — Гадвігера про хроматичне число площини до задач на скінченних графах.
  • Зокрема, з теореми Брёйна — Ердеша і теореми про чотири фарби випливає, що будь-який нескінченний планарний граф допускає розфарбування в чотири кольори.
• Теорему можна узагальнити від скінченного числа кольорів до множини кольорів, кардинальне число якої є строго компактним кардинальним числом.

Теорема де Брейна — Ердеша має кілька різних доведень, кожне з яких використовує аксіому вибору. Початкове доведення де Брейна використовувало трансфінітну індукцію[2].

Готтшальк[3] дав таке дуже коротке доведення, засноване на теоремі про компактність Тихонова в топології. Припустимо, що для заданого нескінченного графу G будь-який скінченний підграф є k-раозфарбовуваним, і нехай X — простір усіх призначень k кольорів вершинам графу G (незалежно від того, чи є це розфарбування правильним). Тоді X можна розглядати як добуток топологічних просторів k^V(G), який, за теоремою Тихонова, компактний. Для кожного скінченного підграфу F графу G нехай X_F — підмножина X що складається з призначень кольорів, які дають правильне розфарбування F. Тоді система множин X_F є сімейством замкнутих множин із властивістю скінченних перетинів, так що через компактності система має непорожній перетин. Будь-який член цього перетину є правильним розфарбуванням G[4].

Інше доведення, що використовує лему Цорна, дав Лайош Поза, а також навів у тезах дисертації (1951) Ендрю Дірак. Якщо G — нескінченний граф, у якому будь-який скінченний підграф є k-розфарбовуваним, тоді, за лемою Цорна, він є підграфом максимального графу M з тією ж властивістю (граф, до якого не можна додати ребра без того, щоб деякий скінченний підграф не зажадав більше k кольорів). Бінарне відношення несуміжності в M є відношенням еквівалентності і класи еквівалентності цього відношення дають k-розфарбування графу G. Однак це доведення складніше узагальнити, ніж доведення за лемою про компактність[5].

Теорему можна довести за допомогою ультрафільтрів[6] або нестандартного аналізу[7]. Неш-Вілльямс[8] дав доведення для графів зі зліченним числом вершин, ґрунтуючись на лемі Кеніга.

Всі доведення теореми де Брейна — Ердеша використовують аксіому вибору. Існують моделі математики, в яких не є істинними ні аксіома вибору, ні теорема де Брейна — Ердеша.

Наприклад, нехай G — нескінченний граф, у якому вершинами є всі дійсні числа. В G з'єднаємо будь-які два дійсних числа x і y ребром, якщо значення (|x − y| ± √2) є раціональним числом. Еквівалентно, в цьому графі, ребра існують між усіма дійсними числами x і всіма числами вигляду x ± (√2 + q) де q — будь раціональне число. Таким чином, якщо дві вершини в G відрізняються на парний цілий множник квадратного кореня з 2 плюс раціональне число, для них можна використовувати один колір і точки можна вважати еквівалентними. Граф, утворений стягуванням класу еквівалентності в одну вершину, є нескінченним паруванням і може бути легко розфарбованим у два кольори, використовуючи аксіому вибору. Таким чином, будь-який скінченний підграф графу G вимагає два кольори. Однак у моделі Соловея, в якій кожна множина дійсних чисел вимірюється за Лебегом, G вимагає нескінченно багато кольорів, оскільки в цьому випадку кожен клас кольору маю бути вимірною множиною, і можна показати, що будь-яка вимірна множина дійсних чисел, що не містить ребер з G, повинна мати міру 0. Таким чином, у моделі Соловея, (необмежене) хроматичне число всього графу G значно більше від хроматичного числа його скінченних підграфів (максимум 2)[9][10].

Можна показати, що теорема де Брейна — Ердеша для зліченних графів еквівалентна (в теорії арифметики другого порядку) лемі Кеніга про нескінченне дерево[11].

Розфарбування площини в сім кольорів і чотириколірний граф одиничних відстаней на площині, що дає верхню і нижню межі для задачі Нельсона — Ердеша — Гадвігера.

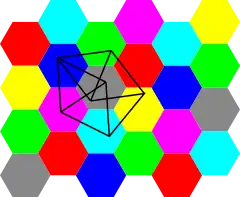
Одне із застосувань теореми де Брейна — Ердеша — це задачі Нельсона — Ердеша — Гадвігера про хроматичне число графу одиничних відстаней евклідової площини. Граф площини має незліченну кількість вершин, по одній на кожну точку площини. Дві вершини пов'язані ребром, коли евклідова відстань між відповідними двома точками дорівнює одиниці. Нескінченний граф має скінченні підграфи, такі як веретено Мозера, які вимагають чотирьох кольорів, і відоме розфарбування в сім кольорів, засноване на шестикутній мозаїці площини. Таким чином, хроматичне число площини має належати множині {4,5,6,7}, але яке з цих чотирьох чисел є дійсно хроматичним числом, невідомо. Теорема де Брейна — Ердеша показує, що для цієї задачі існує скінченний граф одиничних відстаней з тим самим хроматичним числом, що й уся площина цілком, так що, якщо хроматичне число більше чотирьох, то цей факт можна довести скінченними обчисленнями[12].

Теорему де Брейна — Ердеша можна використати також для розширення теореми Ділуорса від скінченного варіанту до нескінченних частково впорядкованих множин. Теорема Ділуорса стверджує, що ширина часткового порядку (найбільше число елементів у множині взаємно непорівнянних елементів) дорівнює мінімальному числу ланцюжків (повністю впорядкованих підмножин), на які можна розкласти частковий порядок. Розкладання на ланцюжки можна розглядати як розфарбування графу непорівнянності часткового порядку (граф, що має вершину для кожного елемента порядку і ребро для кожної пари непорівнянних елементів). Використовуючи цю інтерпретацію як розфарбування, разом з окремим доведенням теореми Ділуорса для скінченних частково впорядкованих множин, можна довести, що нескінченна частково впорядкована множина має скінченну ширину w тоді і тільки тоді, коли його можна розкласти на w ланцюжків[13].

Так само, теорема де Брейна — Ердеша розширює проблему чотирьох фарб зі скінченних планарних графів на нескінченні планарні графи — будь-які графи, які можна намалювати без перетинів на площині, скінченні або нескінченні, можна розфарбувати чотирма фарбами. Загальніше, будь-який нескінченний граф, для якого будь-який скінченний підграф планарний, можна знову розфарбувати в чотири кольори.[14][15]

Теорему де Брейна — Ердеша можна використати для відповіді на питання Гелвіна щодо теореми про проміжне значення для хроматичних чисел графів — для будь-яких двох скінченних чисел j < k і будь-якого графу G з хроматичним числом k існує підграф графу G з хроматичним числом j. Щоб це побачити, знайдемо скінченний підграф графу G з тим самим хроматичним числом, що й сам G, а потім видалятимемо вершини одну за одною, поки не отримаємо хроматичне число j. Однак, випадок для нескінченних хроматичних чисел складніший — це узгоджується з теорією множин, що існує граф з ℵ₂ вершинами і хроматичним числом ℵ₂, який проте не має підграфу з хроматичним числом ℵ₁[16][17].

Радо[18] довів таку теорему, яку можна розглядати як узагальнення теореми де Брёйна — Ердеша. Нехай V — множина, наприклад, множина вершин у нескінченному графі. Для кожного елемента v множини V нехай c_v є скінченною множиною кольорів. Крім того, для будь-якої скінченної підмножини S множини V виберемо деяке розфарбування C_S підмножини S у якому колір кожного елемента v підмножини S належить c_v. Тоді існує глобальне розфарбування χ всіх V з властивістю, що будь-яка скінченна множина S має скінченну супермножину T на якій χ і C_T узгоджуються. Зокрема, якщо ми вибираємо k-розфарбування для будь-якого скінченного підграфу нескінченного графу G тоді існує k-розфарбування графу G в якому кожен скінченний граф має більший суперграф, розфарбування якого узгоджується з розфарбуванням усього графу[19].

Якщо граф не має скінченного хроматичного числа, тоді з теореми де Брейна — Ердеша випливає, що граф має містити скінченні підграфи для кожного можливого хроматичного числа. Дослідники також досліджували інші умови на підграфи. Наприклад, необмежені хроматичні графи повинні також містити будь-який скінченний двочастковий граф як підграф. Однак вони можуть мати довільно великий непарний обхват[20][17].

Теорему де Брейна — Ердеша також можна застосувати безпосередньо до задач розфарбовування гіперграфів, де потрібно, щоб кожне гіперребро мало вершини більше одного кольору. Як і для графів, гіперграф має k-розфарбування тоді і тільки тоді, коли будь-який із його скінченних підгіперграфів має k-розфарбування[21]. Окремий випадок теореми про компактність Курта Геделя стверджує, що множина тверджень першого порядку має модель тоді і тільки тоді, коли будь-яка скінченна підмножина має модель.

Теорему можна узагальнити для випадків, коли число кольорів є нескінченним кардинальним числом — якщо κ є строго компактним кардинальним числом, то для будь-якого графу G і кардинального числа μ < κ, G має хроматичне число, яке не перевищує μ, тоді і тільки тоді, коли його підграфи з кардинальністю меншою від κ мають хроматичне число, яке не перевищує μ[22]. Оригінальна теорема де Брейна — Ердеша є окремим випадком κ = ℵ₀ цього узагальнення, оскільки множина скінченна тоді і тільки тоді, коли її потужність менша ід ℵ_0. Однак деякі припущення, такі як строга компактність кардинального числа множини необхідні — якщо узагальнена континуум-гіпотеза істинна, то для будь-якого нескінченного кардиналу γ існує граф G потужністю (2^γ)⁺, такий, що хроматичне число графу G більше від γ, але будь-який підграф графу G, множина вершин якого має меншу потужність, ніж у G, має хроматичне число, яке не перевищує γ[23]. Лейк[24] описує нескінченні графи, що задовольняють узагальненню теореми де Брейна — Ердеша, як графи, хроматичне число яких дорівнює найбільшому хроматичному числу строго менших підграфів.