Функція правдоподібності

Нехай ${\displaystyle X}$ буде дискретною випадковою змінною з функцією маси ймовірності ${\displaystyle p}$, залежною від параметра ${\displaystyle \theta }$. Тоді функція

${\displaystyle {\mathcal {L}}(\theta \mid x)=p_{\theta }(x)=P_{\theta }(X=x),}$

що розглядають як функцію від ${\displaystyle \theta }$, є функцією правдоподібності для заданого результату ${\displaystyle x}$ випадкової змінної ${\displaystyle X}$. Іноді ймовірність «значення ${\displaystyle x}$ випадкової змінної ${\displaystyle X}$ для значення параметра ${\displaystyle \theta }$» записують як P(X = x | θ) або P(X = x; θ). ${\displaystyle {\mathcal {L}}(\theta \mid x)}$ не слід плутати з ${\displaystyle p(\theta \mid x)}$: правдоподібність дорівнює ймовірності спостерігання певного результату ${\displaystyle x}$, коли справжнім значенням параметра є ${\displaystyle \theta }$, і відтак дорівнює густині ймовірності над результатом ${\displaystyle x}$, а не над параметром ${\displaystyle \theta }$.

Рис. 1.  Функція правдоподібності (${\displaystyle p_{\text{H}}^{2}}$) для ймовірності падіння монети аверсом (англ. heads, H) догори (без попереднього знання про справедливість монети) за умови, що ми проспостерігали HH.

Рис. 2.  Функція правдоподібності (${\displaystyle p_{\text{H}}^{2}(1-p_{\text{H}})}$) для ймовірності падіння монети аверсом (англ. heads, H) догори (без попереднього знання про справедливість монети) за умови, що ми проспостерігали HHT.

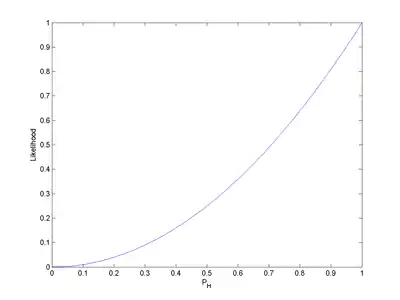
Розгляньмо просту статистичну модель підкидання монети: єдиний параметр ${\displaystyle p_{\text{H}}}$, що виражає «справедливість» цієї монети. Цей параметр є ймовірністю того, що монета після підкидання впаде аверсом (англ. heads, H) догори. ${\displaystyle p_{\text{H}}}$ може набувати будь-якого значення в проміжку з 0.0 по 1.0. Для ідеально справедливої монети ${\displaystyle p_{\text{H}}=0.5}$.

Уявімо підкидання справедливої монети двічі, й спостерігання наступних даних: два аверси за два підкидання (HH). Якщо виходити з припущення, що кожне наступне підкидання монети є н. о. р., то ймовірністю спостерігання HH є

${\displaystyle P({\text{HH}}\mid p_{\text{H}}=0.5)=0.5^{2}=0.25.}$

Отже, за заданих даних спостережень HH, правдоподібністю того, що параметр моделі ${\displaystyle p_{\text{H}}}$ дорівнює 0.5, є 0.25. Математично це записують як

${\displaystyle {\mathcal {L}}(p_{\text{H}}=0.5\mid {\text{HH}})=0.25.}$

Це не те ж саме, що й сказати, що ймовірністю того, що ${\displaystyle p_{\text{H}}=0.5}$, за заданого спостереження HH є 0.25. (Для цього ми можемо застосувати теорему Баєса, яка означає, що апостеріорна ймовірність є пропорційною до правдоподібності, помноженої на апріорну ймовірність.)

Припустімо, що ця монета не є справедливою, але натомість має ${\displaystyle p_{\text{H}}=0.3}$. Тоді ймовірністю отримання двох аверсів є

${\displaystyle P({\text{HH}}\mid p_{\text{H}}=0.3)=0.3^{2}=0.09.}$

Отже,

${\displaystyle {\mathcal {L}}(p_{\text{H}}=0.3\mid {\text{HH}})=0.09.}$

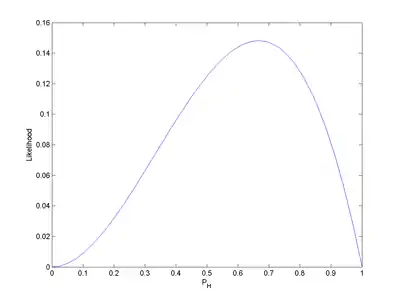
Загальніше, для кожного значення ${\displaystyle p_{\text{H}}}$ ми можемо обчислити відповідну правдоподібність. Результати таких обчислень показано на Рис. 1.

На Рис. 1. інтегралом правдоподібності над проміжком [0, 1] є 1/3. Це висвітлює важливий аспект правдоподібностей: правдоподібності не мають інтегруватися (чи підсумовуватися) до 1, на відміну від імовірностей.

Нехай ${\displaystyle X}$ буде випадковою змінною, що слідує абсолютно неперервному розподілові ймовірності з функцією густини ${\displaystyle f}$, залежною від параметра ${\displaystyle \theta }$. Тоді функція

${\displaystyle {\mathcal {L}}(\theta \mid x)=f_{\theta }(x)=p(X=x\mid \theta ),\,}$

що розглядають як функцію від ${\displaystyle \theta }$, є функцією правдоподібності (параметра ${\displaystyle \theta }$ для заданого результату ${\displaystyle x}$ змінної ${\displaystyle X}$). Іноді функцію густини для «значення ${\displaystyle x}$ змінної ${\displaystyle X}$ для значення параметра ${\displaystyle \theta }$» записують як ${\displaystyle f(x\mid \theta )}$. ${\displaystyle {\mathcal {L}}(\theta \mid x)}$ не слід плутати з ${\displaystyle p(\theta \mid x)}$: правдоподібність дорівнює густині ймовірності на певному результаті ${\displaystyle x}$, коли справжнім значенням параметра є ${\displaystyle \theta }$, і відтак вона дорівнює густині ймовірності над результатом ${\displaystyle x}$, а не над параметром ${\displaystyle \theta }$.

В теорії ймовірностей на основі теорії мір функцію густини означують як похідну Радона — Нікодима розподілу ймовірності відносно спільної домінантної міри.[7] Функція правдоподібності є цією густиною, інтерпретованою як функція від параметра (можливо, векторного), а не від можливих результатів.[8] Це забезпечує функцію правдоподібності для будь-якої статистичної моделі з усіма розподілами, чи то дискретними, абсолютно неперервними, сумішшю, чи чимось ще. (Правдоподібності буде можливо порівнювати, наприклад, для оцінювання параметрів, лише якщо вони є похідними Радона — Нікодима по відношенню до однієї й тієї ж домінантної міри.)

Наведене вище обговорення правдоподібності з дискретними ймовірностями є окремим випадком цього із застосуванням лічильної міри, яка робить імовірність будь-якого одиничного результату рівною густині ймовірності для цього результату.

Якщо не задано жодної події (немає даних), то ймовірністю, і відтак правдоподібністю, є 1.^{[джерело?]} Будь-яка нетривіальна подія матиме нижчу правдоподібність.

Із багатьох застосувань ми розглянемо тут одне, що має широку теоретичну та практичну важливість. Для заданого параметризованого сімейства функцій густини ймовірності (або функцій маси ймовірності у випадку дискретних розподілів)

${\displaystyle x\mapsto f(x\mid \theta ),\!}$

де ${\displaystyle \theta }$ є параметром, фу́нкцією правдоподі́бності (англ. likelihood function) є

${\displaystyle \theta \mapsto f(x\mid \theta ),\!}$

що записують як

${\displaystyle {\mathcal {L}}(\theta \mid x)=f(x\mid \theta ),\!}$

де ${\displaystyle x}$ є спостережуваним результатом експерименту. Іншими словами, коли ${\displaystyle f(x|\theta )}$ розглядають як функцію від ${\displaystyle x}$ за незмінного ${\displaystyle \theta }$, вона є функцією густини ймовірності, а коли її розглядають як функцію від ${\displaystyle \theta }$ за незмінного ${\displaystyle x}$, вона є функцією правдоподібності.

Це не є тим же, що й імовірність того, що ці параметри є правильними за заданої спостережуваної вибірки. Намагання інтерпретувати правдоподібність гіпотези за заданого спостережуваного свідчення як її імовірність є поширеною помилкою з потенційно катастрофічними наслідками. Як приклад цього див. хибу обвинувача.

З геометричної точки зору, якщо ми розглядаємо ${\displaystyle f(x|\theta )}$ як функцію від двох змінних, то сімейство розподілів імовірності можливо розглядати як сімейство кривих, паралельних до осі ${\displaystyle x}$, тоді як сімейство функцій правдоподібності є перпендикулярними кривими, паралельними до осі ${\displaystyle \theta }$.

Застосування густини ймовірності у визначенні функції правдоподібності вище може бути пояснено наступним чином. Для заданих спостережень ${\displaystyle x_{j}}$ правдоподібність для проміжку ${\displaystyle [x_{j},x_{j}+h]}$, де ${\displaystyle h>0}$ є сталою, задають як ${\displaystyle {\mathcal {L}}(\theta \mid x\in [x_{j},x_{j}+h])}$. Зверніть увагу, що

${\displaystyle \operatorname {argmax} _{\theta }{\mathcal {L}}(\theta \mid x\in [x_{j},x_{j}+h])=\operatorname {argmax} _{\theta }{\frac {1}{h}}{\mathcal {L}}(\theta \mid x\in [x_{j},x_{j}+h])}$,

оскільки ${\displaystyle h}$ є додатною та сталою. Оскільки

${\displaystyle \operatorname {argmax} _{\theta }{\frac {1}{h}}{\mathcal {L}}(\theta \mid x\in [x_{j},x_{j}+h])=\operatorname {argmax} _{\theta }{\frac {1}{h}}\Pr(x_{j}\leq x\leq x_{j}+h\mid \theta )=\operatorname {argmax} _{\theta }{\frac {1}{h}}\int _{x_{j}}^{x_{j}+h}f(x\mid \theta )\,dx,}$

де ${\displaystyle f(x\mid \theta )}$ є функцією густини ймовірності, з цього випливає, що

${\displaystyle \operatorname {argmax} _{\theta }{\mathcal {L}}(\theta \mid x\in [x_{j},x_{j}+h])=\operatorname {argmax} _{\theta }{\frac {1}{h}}\int _{x_{j}}^{x_{j}+h}f(x\mid \theta )\,dx}$.

Перша фундаментальна теорема інтегрального числення та правило Лопіталя разом забезпечують, що

${\displaystyle {\begin{aligned}&\lim _{h\to 0^{+}}{\frac {1}{h}}\int _{x_{j}}^{x_{j}+h}f(x\mid \theta )\,dx=\lim _{h\to 0^{+}}{\frac {{\frac {d}{dh}}\int _{x_{j}}^{x_{j}+h}f(x\mid \theta )\,dx}{\frac {dh}{dh}}}\\[4pt]={}&\lim _{h\to 0^{+}}{\frac {f(x_{j}+h\mid \theta )}{1}}=f(x_{j}\mid \theta ).\end{aligned}}}$

Тоді

${\displaystyle {\begin{aligned}&\operatorname {argmax} _{\theta }{\mathcal {L}}(\theta \mid x_{j})=\operatorname {argmax} _{\theta }\left[\lim _{h\to 0^{+}}{\mathcal {L}}(\theta \mid x\in [x_{j},x_{j}+h])\right]\\[4pt]={}&\operatorname {argmax} _{\theta }\left[\lim _{h\to 0^{+}}{\frac {1}{h}}\int _{x_{j}}^{x_{j}+h}f(x\mid \theta )\,dx\right]=\operatorname {argmax} _{\theta }f(x_{j}\mid \theta ).\end{aligned}}}$

Отже,

${\displaystyle \operatorname {argmax} _{\theta }{\mathcal {L}}(\theta \mid x_{j})=\operatorname {argmax} _{\theta }f(x_{j}\mid \theta ),\!}$

і відтак максимізування густини ймовірності в ${\displaystyle x_{j}}$ є рівносильним максимізуванню правдоподібності конкретного спостереження ${\displaystyle x_{j}}$.

Наведене вище може бути в простий спосіб розширено так, щоби дозволяти розгляд розподілів, що містять як дискретні, так і неперервні складові. Припустімо, що такий розподіл складається з якоїсь кількості дискретних мас імовірності ${\displaystyle p_{k}\theta }$ та з густини ${\displaystyle f(x|\theta )}$, де сума всіх ${\displaystyle p}$, додана до інтегралу ${\displaystyle f}$, завжди є одиницею. За припущення, що можливо розрізняти спостереження, що відповідає одній з цих дискретних мас імовірності, від того, що відповідає складовій густини, функцію правдоподібності для спостереження з неперервної складової можливо розглядати наведеним вище чином. Для спостереження з дискретної складової функцією правдоподібності для спостереження з цієї дискретної складової є просто

${\displaystyle {\mathcal {L}}(\theta \mid x)=p_{k}(\theta ),\!}$

де ${\displaystyle k}$ є індексом маси дискретної ймовірності, що відповідає спостереженню ${\displaystyle x}$, оскільки максимізування маси ймовірності (або ймовірності) в ${\displaystyle x}$ є рівносильним максимізуванню правдоподібності цього конкретного спостереження.

Той факт, що функцію правдоподібності може бути визначено в спосіб, що включає не порівнянні внески (густина та маса ймовірності), випливає зі способу її визначення, в якому функцію правдоподібності визначено з точністю до сталої пропорційності, де ця «стала» може змінюватися зі спостереженням ${\displaystyle x}$, але не з параметром ${\displaystyle \theta }$.

В контексті оцінювання параметрів зазвичай виходять з того, що функція правдоподібності задовольняє певні умови, відомі як умови регулярності (англ. regularity conditions). З цих умов виходять у багатьох доведеннях, що включають функції правдоподібності, і їх потрібно перевіряти в кожному конкретному застосуванні. Для методу максимальної правдоподібності надзвичайно важливим є існування глобального максимуму функції правдоподібності. Згідно другої теореми Веєрштраса, неперервна функція правдоподібності на компактному просторі параметрів є достатньою для існування оцінювача максимальною правдоподібністю.[9] В той час як припущення про неперервність зазвичай виконується, припущення про компактність простору параметрів часто не виконується, оскільки межі справжніх значень параметрів є невідомими. В такому випадку ключову роль відіграє угнутість функції правдоподібності.

Конкретніше, якщо функція правдоподібності є двічі неперервно диференційовною на k-вимірному просторі параметрів ${\displaystyle \Theta }$, що вважають відкритою зв'язаною підмножиною ${\displaystyle \mathbb {R} ^{k}}$, то унікальний максимум ${\displaystyle {\hat {\theta }}\in \Theta }$ існує, якщо

${\displaystyle \mathbf {H} (\theta )=\left\{{\frac {\partial ^{2}L}{\partial \theta _{i}\partial \theta _{j}}}\right\}}$ є від'ємно визначеною для кожного ${\displaystyle \theta \in \Theta }$, для якого градієнт ${\displaystyle \nabla L=\left\{\partial L/\partial \theta _{i}\right\}}$ зникає, та

${\displaystyle \lim _{\theta \to \partial \Theta }L(\theta )=0}$, тобто функція правдоподібності наближується до сталої на межі простору параметрів, яка може включати точки на нескінченності, якщо ${\displaystyle \Theta }$ є необмеженим.

Макелайнен та ін. доводять цей результат, застосовуючи теорію Морса, неформально звертаючись до властивості гірського перевалу.[10] Машкареньяш підтверджує їхнє доведення, застосовуючи теорему про гірський перевал.[11]

В доведенні слушності та асимптотичної нормальності оцінювача максимальною правдоподібністю роблять додаткові припущення про густи́ни ймовірностей, які складають основу певної функції правдоподібності. Ці умови було вперше встановлено Чандою.[12] Зокрема, для майже всіх ${\displaystyle x}$, та для всіх ${\displaystyle \theta \in \Theta }$

${\displaystyle {\frac {\partial \log f}{\partial \theta _{r}}}\,,\quad {\frac {\partial ^{2}\log f}{\partial \theta _{r}\partial \theta _{s}}}\,,\quad {\frac {\partial ^{3}\log f}{\partial \theta _{r}\partial \theta _{s}\partial \theta _{t}}}}$

існують для всіх ${\displaystyle r,s,t=1,2,\ldots ,k}$, щоби забезпечити існування розкладу Тейлора. По-друге, для майже всіх ${\displaystyle x}$ та для кожного ${\displaystyle \theta \in \Theta }$ мусить бути

${\displaystyle \left|{\frac {\partial f}{\partial \theta _{r}}}\right|<F_{r}(x)\,,\quad \left|{\frac {\partial ^{2}f}{\partial \theta _{r}\partial \theta _{s}}}\right|<F_{rs}(x)\,,\quad \left|{\frac {\partial ^{3}f}{\partial \theta _{r}\partial \theta _{s}\partial \theta _{t}}}\right|<H_{rst}(x)}$

де ${\displaystyle H}$ є такою, що ${\displaystyle \int _{-\infty }^{\infty }H_{rst}(z)\mathrm {d} z\leq M<\infty }$. Ця обмеженість похідних є потрібною, щоби уможливити диференціювання під знаком інтегралу. І, нарешті, передбачається, що інформаційна матриця

${\displaystyle \mathbf {I} (\theta )=\int _{-\infty }^{\infty }{\frac {\partial \log f}{\partial \theta _{r}}}{\frac {\partial \log f}{\partial \theta _{s}}}f\mathrm {d} z}$

є додатно визначеною, а ${\displaystyle \left|\mathbf {I} (\theta )\right|}$ є скінченною. Це забезпечує скінченність дисперсії внеску.[13]

Наведені вище умови є достатніми, але не необхідними. Тобто, модель, що не задовольняє ці умови регулярності, може мати, а може й не мати оцінювача максимальною правдоподібністю згаданих вище властивостей. Крім того, у випадку не незалежно або не однаково розподілених спостережень може бути потрібно очікувати додаткових властивостей.

Відно́шення правдоподі́бностей (англ. likelihood ratio) — це відношення будь-яких двох вказаних правдоподібностей, що часто записують як

${\displaystyle \Lambda (\theta _{1}:\theta _{2}\mid x)={\frac {{\mathcal {L}}(\theta _{1}\mid x)}{{\mathcal {L}}(\theta _{2}\mid x)}}}$

Відношення правдоподібностей є центральним для правдоподібницької статистики: закон правдоподібності встановлює, що ступінь, до якого дані (що розглядають як свідчення) підтримують один параметр проти іншого, вимірюється відношенням правдоподібностей.

В частотницькому висновуванні відношення правдоподібності є основою для статистичного критерію, так званої перевірки відношенням правдоподібностей. Згідно леми Неймана — Пірсона, вона є найпотужнішою перевіркою для порівнювання двох простих гіпотез на заданому рівні значущості. Численні інші критерії можливо розглядати як перевірки відношенням правдоподібностей, або його наближеннями.[14] Асимптотичний розподіл логарифмічного відношення правдоподібностей, що розглядають як статистичний критерій, задано теоремою Уілкса.

Відношення правдоподібностей також має центральне значення в баєсовім висновуванні, де воно є відомим як коефіцієнт Баєса, і застосовується в правилі Баєса. Викладене в термінах шансів (англ. odds), правило Баєса полягає в тім, що апостеріорні шанси двох альтернатив, ${\displaystyle A_{1}}$ та ${\displaystyle A_{2}}$, за умови події ${\displaystyle B}$, є апріорними шансами, помноженими на відношення правдоподібностей. У вигляді рівняння:

${\displaystyle O(A_{1}:A_{2}\mid B)=O(A_{1}:A_{2})\cdot \Lambda (A_{1}:A_{2}\mid B).}$

Відношення правдоподібності не використовують в статистиці на основі ІКА напряму. Натомість використовують відносну правдоподібність моделей (див. нижче).

Відношення правдоподібностей двох моделей, коли задано одну й ту ж подію, може бути протиставлено з шансами двох подій, коли задано одну й ту ж модель. В термінах параметризованої функції маси ймовірності ${\displaystyle p_{\theta }(x)}$, відношенням правдоподібностей двох параметрів ${\displaystyle \theta _{1}}$ та ${\displaystyle \theta _{2}}$ за заданого результату ${\displaystyle x}$ є

${\displaystyle \Lambda (\theta _{1}:\theta _{2}\mid x)=p_{\theta _{1}}(x):p_{\theta _{2}}(x),}$

тоді як шансами двох результатів, ${\displaystyle x_{1}}$ та ${\displaystyle x_{2}}$, за заданого значення параметра ${\displaystyle \theta }$, є

${\displaystyle O(x_{1}:x_{2}\mid \theta )=p_{\theta }(x_{1}):p_{\theta }(x_{2}).}$

Це підкреслює різницю між правдоподібностями та шансами: в правдоподібностях порівнюють моделі (параметри), тримаючи дані незмінними, тоді як в шансах порівнюють події (результати, дані), тримаючи незмінною модель.

Відношення шансів є відношенням двох умовних шансів (події, за заданої присутності або відсутності іншої події). Проте відношення шансів також можливо інтерпретувати як відношення двох відношень правдоподібностей, якщо розглядати одну з подій як спостережувану легше за іншу. Див. діагностичне відношення шансів, де результат перевірки для встановлення діагнозу спостерігати легше, ніж наявність або відсутність медичного стану, що лежить в його основі.

Оскільки фактичне значення функції правдоподібності залежить від вибірки, часто зручно працювати зі стандартизованою мірою. Припустімо, що оцінкою максимальною правдоподібністю для параметра θ є ${\displaystyle {\hat {\theta }}}$. Відносні вірогідності (англ. plausibilities) інших значень θ може бути знайдено порівнюванням правдоподібностей цих інших значень з правдоподібністю ${\displaystyle {\hat {\theta }}}$. Відно́сну правдоподі́бність (англ. relative likelihood) θ означують як[15][16][17][18][19]

${\displaystyle R(\theta )={\frac {{\mathcal {L}}(\theta \mid x)}{{\mathcal {L}}({\hat {\theta }}\mid x)}}.}$

Таким чином, відносна правдоподібність є відношенням правдоподібностей (обговореним вище) з незмінним знаменником ${\displaystyle {\mathcal {L}}({\hat {\theta }})}$. Це відповідає унормуванню цієї правдоподібності, щоби вона мала за максимум 1.

О́бласть правдоподі́бності (англ. likelihood region) — це множина всіх значень θ, чиї відносні правдоподібності є більшими або рівними заданому порогові. В термінах відсотків, p%-ву область правдоподібності для θ означують як[15][17][20]

${\displaystyle \left\{\theta :R(\theta )\geq {\frac {p}{100}}\right\}.}$

Якщо θ є єдиним дійснозначним параметром, то p%-ва область правдоподібності зазвичай становить проміжок дійсних значень. Якщо ця область дійсно становить проміжок, то її називають про́міжком правдоподі́бності (англ. likelihood interval).[15][17][21]

Проміжки правдоподібності, та, загальніше, області правдоподібності використовують для проміжкового оцінювання в правдоподібницькій статистиці: вони є подібними до довірчих проміжків у частотницькій статистиці та ймовірних проміжків у баєсовій статистиці. Проміжки правдоподібності тлумачать безпосередньо в термінах відносної правдоподібності, а не в термінах ймовірності накриття (частотництво) чи апостеріорної ймовірності (баєсівство).

Для заданої моделі проміжки правдоподібності можливо порівнювати з довірчими проміжками. Якщо θ є єдиним дійснозначним параметром, то, за певних умов 14.65%-й проміжок правдоподібності (правдоподібність близько 1:7) для θ буде таким же, як і 95%-й довірчий проміжок (ймовірність накриття 19/20).[15][20] У дещо відмінному формулюванні, пристосованому для використання логарифмічних правдоподібностей (див. теорему Уілкса), перевірна статистика є подвоєною різницею логарифмічних правдоподібностей, а розподіл імовірності цієї перевірної статистики приблизно є розподілом хі-квадрат зі ступенями вільності, що дорівнюють різниці в ступенях вільності між цими двома моделями (тому проміжок правдоподібності e⁻² є таким же, як і довірчий проміжок 0.954, за припущення, що різницею в ступенях вільності є 1).[20][21]

Можливо знижувати розмірності, зосереджуючи функцію правдоподібності на підмножині параметрів шляхом виражання завадних параметрів як функцій від параметрів, що становлять інтерес, і заміни їх у функції правдоподібності.[24][25] Загалом, для функції правдоподібності, що залежить від вектору параметрів ${\displaystyle \mathbf {\theta } }$, який можливо розбити на ${\displaystyle \mathbf {\theta } =\left(\mathbf {\theta } _{1}:\mathbf {\theta } _{2}\right)}$, і де відповідність ${\displaystyle \mathbf {\hat {\theta }} _{2}=\mathbf {\hat {\theta }} _{2}\left(\mathbf {\theta } _{1}\right)}$ можливо визначити явно, зосереджування знижує обчислювальне навантаження первинної задачі максимізації.[26]

Наприклад, в лінійній регресії з нормально розподіленими похибками, ${\displaystyle \mathbf {y} =\mathbf {X} \beta +u}$, вектор коефіцієнтів може бути розбито на ${\displaystyle \beta =\left[\beta _{1}:\beta _{2}\right]}$ (а матрицю плану, відповідно, на ${\displaystyle \mathbf {X} =\left[\mathbf {X} _{1}:\mathbf {X} _{2}\right]}$). Максимізування відносно ${\displaystyle \beta _{2}}$ видає функцію оптимального значення ${\displaystyle \beta _{2}(\beta _{1})=\left(\mathbf {X} _{2}^{\mathsf {T}}\mathbf {X} _{2}\right)^{-1}\mathbf {X} _{2}^{\mathsf {T}}\left(\mathbf {y} -\mathbf {X} _{1}\beta _{1}\right)}$. Із застосуванням цього результату оцінювач максимальною правдоподібністю для ${\displaystyle \beta _{1}}$ може бути виведено як

${\displaystyle {\hat {\beta }}_{1}=\left(\mathbf {X} _{1}^{\mathsf {T}}\left(\mathbf {I} -\mathbf {P} _{2}\right)\mathbf {X} _{1}\right)^{-1}\mathbf {X} _{1}^{\mathsf {T}}\left(\mathbf {I} -\mathbf {P} _{2}\right)\mathbf {y} }$

де ${\displaystyle \mathbf {P} _{2}=\mathbf {X} _{2}\left(\mathbf {X} _{2}^{\mathsf {T}}\mathbf {X} _{2}\right)^{-1}\mathbf {X} _{2}^{\mathsf {T}}}$ є проєктивною матрицею ${\displaystyle \mathbf {X} _{2}}$. Цей результат є відомим як теорема Фріша — Во — Ловелла.

Оскільки графічно процедура зосереджування є рівнозначною нарізанню поверхні правдоподібності по хребту значень завадного параметра ${\displaystyle \beta _{2}}$, яке максимізує функцію правдоподібності, створюючи ізометричний профіль функції правдоподібності для заданого ${\displaystyle \beta _{1}}$, результат цієї процедури є також відомим як про́фільна правдоподі́бність (англ. profile likelihood).[27][28] На додачу до графічного зображування, профільну правдоподібність також можливо використовувати для обчислювання довірчих проміжків, які часто мають кращі властивості на малих вибірках, ніж основані на асимптотичних стандартних похибках, обчислюваних із повної правдоподібності.[29][30]

Іноді для завадних параметрів можливо знайти достатню статистику, і обумовлювання цією статистикою дає в результаті правдоподібність, що не залежить від завадних параметрів.[31]

Один із прикладів трапляється в таблицях 2×2, де обумовлювання усіма чотирма відособленими підсумками веде до умовної правдоподібності на основі нецентрального гіпергеометричного розподілу. Цей вид обумовлювання є також основою точного тесту Фішера.

Іноді ми можемо усувати завадні параметри, розглядаючи правдоподібність на основі лише частини інформації з даних, наприклад, застосуванням набору порядків замість числових значень. Інший приклад трапляється в лінійних змішаних моделях, де розгляд правдоподібності лише для залишків після допасовування фіксованих впливів веде до оцінювання залишковою максимальною правдоподібністю складових відхилення.

Часткова правдоподібність (англ. partial likelihood) — це таке пристосування повної правдоподібності, що в ньому має місце лише частина параметрів (параметри, що становлять інтерес).[32] Вона є ключовою складовою моделі пропорційних ризиків: з використанням обмеження на функцію ризиків, правдоподібність не містить фігури ризику в часі.

Якщо функція логарифмічної правдоподібності є гладкою, то її градієнт відносно параметра, відомий як внесок і записуваний як ${\displaystyle s_{n}(\theta )\equiv \nabla _{\theta }\ell _{n}(\theta )}$, існує й дозволяє застосовувати диференціальне числення. Базовим способом максимізувати диференційовну функцію є знаходити стаціонарні точки (такі, де її похідна є нульовою). Оскільки похідна суми є просто сумою похідних, а похідна добутку вимагає правила добутку, простіше обчислювати стаціонарні точки логарифмічної правдоподібності окремих подій, ніж правдоподібності окремих подій.

Рівняння, що визначає стаціонарна точка функції внеску, слугують оцінними рівняннями для оцінювача максимальною правдоподібністю.

${\displaystyle s_{n}(\theta )=\mathbf {0} }$

В цьому сенсі оцінювач максимальною правдоподібністю неявно визначається значенням в ${\displaystyle \mathbf {0} }$ оберненої функції ${\displaystyle s_{n}^{-1}:\mathbb {E} ^{d}\to \Theta }$, де ${\displaystyle \mathbb {E} ^{d}}$ є d-вимірним евклідовим простором. Шляхом застосування теореми про обернену функцію можливо показати, що ${\displaystyle s_{n}^{-1}}$ є однозначно означеною у відкритому околі навколо ${\displaystyle \mathbf {0} }$ з імовірністю, що прямує до одиниці, а ${\displaystyle {\hat {\theta }}_{n}=s_{n}^{-1}(\mathbf {0} )}$ є слушною оцінкою ${\displaystyle \theta }$. Як наслідок, існує така послідовність ${\displaystyle \left\{{\hat {\theta }}_{n}\right\}}$, що ${\displaystyle s_{n}({\hat {\theta }}_{n})=\mathbf {0} }$ асимптотично майже напевно, і ${\displaystyle {\hat {\theta }}_{n}{\xrightarrow {\text{p}}}\theta _{0}}$.[35] Аналогічний результат можливо встановити, застосувавши теорему Ролля.[36][37]

Друга похідна, обчислювана в ${\displaystyle {\hat {\theta }}}$, відома як інформація за Фішером, визначає кривину поверхні правдоподібності,[38] і відтак показуючи прецизійність оцінки.[39]

Логарифмічна правдоподібність є також надзвичайно корисною для експоненційних сімейств розподілів, до яких можуть входити багато поширених параметричних розподілів імовірностей. Функція розподілу ймовірності (й відтак функція правдоподібності) для експоненційних сімейств містить добутки множників, що містять піднесення до степеня. Логарифм такої функції є сумою добутків, знов-таки простішою для диференціювання за первинну функцію.

Експоненційне сімейство — це таке, чия функція густини ймовірності має вигляд (для деяких функцій, із позначенням через ${\displaystyle \langle -,-\rangle }$ внутрішнього добутку):

${\displaystyle p(x\mid {\boldsymbol {\theta }})=h(x)\exp {\Big (}\langle {\boldsymbol {\eta }}({\boldsymbol {\theta }}),\mathbf {T} (x)\rangle -A({\boldsymbol {\theta }}){\Big )}.}$

Кожен із цих членів має інтерпретацію,[lower-alpha 4] але простий перехід від імовірності до правдоподібності та взяття логарифмів дає суму

${\displaystyle \ell ({\boldsymbol {\theta }}\mid x)=\langle {\boldsymbol {\eta }}({\boldsymbol {\theta }}),\mathbf {T} (x)\rangle -A({\boldsymbol {\theta }})+\log h(x).}$

${\displaystyle {\boldsymbol {\eta }}({\boldsymbol {\theta }})}$ та ${\displaystyle h(x)}$ відповідають зміні координат, тож у цих координатах логарифмічна правдоподібність експоненційного сімейства задається простою формулою

${\displaystyle \ell ({\boldsymbol {\eta }}\mid x)=\langle {\boldsymbol {\eta }},\mathbf {T} (x)\rangle -A({\boldsymbol {\eta }}).}$

Словами, логарифмічна правдоподібність експоненційного сімейства є внутрішнім добутком природного параметра ${\displaystyle {\boldsymbol {\eta }}}$ та достатньої статистики ${\displaystyle \mathbf {T} (x)}$, мінус коефіцієнт унормування (логарифмічна статистична сума) ${\displaystyle A({\boldsymbol {\eta }})}$. Таким чином, наприклад, оцінку максимальною правдоподібністю може бути обчислено взяттям похідних достатньої статистики T та логарифмічної статистичної суми A.

Гамма-розподіл — це експоненційне сімейство з двома параметрами, ${\displaystyle \alpha }$ та ${\displaystyle \beta }$. Його функцією правдоподібності є

${\displaystyle {\mathcal {L}}(\alpha ,\beta \mid x)={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}x^{\alpha -1}e^{-\beta x}.}$

Знаходження оцінки максимальної правдоподібності ${\displaystyle \beta }$ для єдиного спостережуваного значення ${\displaystyle x}$ виглядає дещо складним. З його логарифмом працювати набагато простіше:

${\displaystyle \log {\mathcal {L}}(\alpha ,\beta \mid x)=\alpha \log \beta -\log \Gamma (\alpha )+(\alpha -1)\log x-\beta x.\,}$

Щоби максимізувати логарифмічну правдоподібність, ми спершу беремо часткову похідну за ${\displaystyle \beta }$:

${\displaystyle {\frac {\partial \log {\mathcal {L}}(\alpha ,\beta \mid x)}{\partial \beta }}={\frac {\alpha }{\beta }}-x.}$

Якщо є ряд незалежних спостережень ${\displaystyle x_{1},\ldots ,x_{n}}$, то спільною логарифмічною правдоподібністю буде сума окремих логарифмічних правдоподібностей, а похідною цієї суми буде сума похідних всіх окремих логарифмічних правдоподібностей:

${\displaystyle {\begin{aligned}&{\frac {\partial \log {\mathcal {L}}(\alpha ,\beta \mid x_{1},\ldots ,x_{n})}{\partial \beta }}\\={}&{\frac {\partial \log {\mathcal {L}}(\alpha ,\beta \mid x_{1})}{\partial \beta }}+\cdots +{\frac {\partial \log {\mathcal {L}}(\alpha ,\beta \mid x_{n})}{\partial \beta }}={\frac {n\alpha }{\beta }}-\sum _{i=1}^{n}x_{i}.\end{aligned}}}$

Щоби завершити процедуру максимізування для спільної логарифмічної правдоподібності, це рівняння встановлюють в нуль, і розв'язують для ${\displaystyle \beta }$:

${\displaystyle {\widehat {\beta }}={\frac {\alpha }{\bar {x}}}.}$

Тут ${\displaystyle {\widehat {\beta }}}$ позначує оцінку максимальною правдоподібністю, а ${\displaystyle \textstyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$ є вибірковим середнім спостережень.

Термін англ. likelihood (правдоподібність) був у вжитку в англійській щонайменше з середньоанглійської.[40] Його формальне застосування для позначення конкретної функції в математичній статистиці було запропоновано Рональдом Фішером[41] у двох дослідницьких працях, опублікованих 1921[42] та 1922[43] року. Праця 1921 року запровадила те, що тепер називають «проміжком правдоподібності». Праця 1922 року запровадила термін «метод максимальної правдоподібності». Цитуючи Фішера,

1922 року я запропонував термін «правдоподібність», з огляду на той факт, що по відношенню до [параметра], вона не є ймовірністю, й не підкоряється законам імовірності, в той же час привносячи до задачі раціонального обирання серед можливих значень [параметра] відношення, подібне до того, що ймовірність привносить до задачі передбачування подій в іграх випадку... Проте, в той час як по відношенню до психологічного судження правдоподібність має певну схожість з імовірністю, ці два поняття є цілком різними... Оригінальний текст (англ.) [I]n 1922, I proposed the term ‘likelihood,’ in view of the fact that, with respect to [the parameter], it is not a probability, and does not obey the laws of probability, while at the same time it bears to the problem of rational choice among the possible values of [the parameter] a relation similar to that which probability bears to the problem of predicting events in games of chance....Whereas, however, in relation to psychological judgment, likelihood has some resemblance to probability, the two concepts are wholly distinct....” [44]

Поняття правдоподібності не слід плутати з імовірністю, як зазначено сером Рональдом Фішером,

Я наголошую на цьому, оскільки, незважаючи на наголос, який я завжди робив на відмінності між імовірністю та правдоподібністю, все ще існує тенденція ставитися до правдоподібності так, ніби вона є чимось на кшталт імовірності. Першим результатом відтак є те, що існує дві різні міри раціонального переконання, що відповідають різним випадкам. Знаючи сукупність, ми можемо виражати наше неповне знання або наші неповні очікування про вибірку в термінах імовірності; знаючи вибірку, ми можемо виражати наші неповні знання про сукупність у термінах правдоподібності. Оригінальний текст (англ.) I stress this because in spite of the emphasis that I have always laid upon the difference between probability and likelihood there is still a tendency to treat likelihood as though it were a sort of probability. The first result is thus that there are two different measures of rational belief appropriate to different cases. Knowing the population we can express our incomplete knowledge of, or expectation of, the sample in terms of probability; knowing the sample we can express our incomplete knowledge of the population in terms of likelihood. [45]

Фішерове винайдення статистичної правдоподібності було реакцією на раніший вид міркування, званий оберненою ймовірністю.[46] Його застосування терміну «правдоподібність» зафіксувало значення цього терміну в межах математичної статистики.

Е. В. Ф. Едвардс (1972) заклав аксіоматичну основу для застосування логарифмічного відношення правдоподібностей як міри відносної підтри́мки (англ. support) однієї гіпотези проти іншої. Фу́нкцією підтри́мки (англ. support function) в такому разі є натуральний логарифм функції правдоподібності. Обидва терміни застосовують у філогенетиці, але їх не були прийнято в загальному трактуванні теми статистичних даних.[47]

Серед статистиків нема єдиної думки про те, якими повинні бути засади статистики. Існує чотири головні парадигми, які було запропоновано як засади: частотництво, баєсівство, правдоподібництво, та на основі ІКА.[6] Для кожних із цих запропонованих засад інтерпретація правдоподібності є різною. Ці чотири інтерпретації описано в підрозділах нижче.

У баєсовім висновуванні, хоча й можливо говорити про правдоподібність будь-якого висловлення чи випадкової змінної за заданої іншої випадкової змінної, наприклад, про правдоподібність значення параметра чи статистичної моделі (див. відособлену правдоподібність) за заданих даних або іншого свідчення,[48][49][50][51] функція правдоподібності залишається тією ж сутністю з додатковими інтерпретаціями (i) умовної густини ймовірності даних за заданого параметра (оскільки параметр тоді є випадковою змінною), та (ii) міри кількості інформації, що несуть дані про значення параметра або навіть про модель.[48][49][50][51][52] Внаслідок введення ймовірнісної структури на просторі параметрів або сукупності моделей є можливим, щоби значення параметра або статистична модель мали велике значення правдоподібності для заданих даних, але в той же час низьку ймовірність, і навпаки.[50][52] Таке часто трапляється в контексті медицини.[53] Згідно правила Баєса, правдоподібність, коли розглядати її як умовну густину, можливо множини на густину апріорної ймовірності параметра й потім унормовувати, щоби отримувати густину апостеріорної ймовірності.[48][49][50][51][52] Загальніше, правдоподібність невідомої величини ${\displaystyle X}$ за заданої іншої невідомої величини ${\displaystyle Y}$ є пропорційною до ймовірності ${\displaystyle Y}$ за заданої ${\displaystyle X}$.[48][49][50][51][52]

У частотницькій статистиці функція правдоподібності сама по собі є статистикою, яка узагальнює окремий зразок із сукупності, й чиє обчислюване значення залежить від вибору декількох параметрів θ₁... θ_p, де p є кількістю параметрів у якійсь вже обраній статистичній моделі. Значення правдоподібності слугує критерієм якості для вибору, зробленого для параметрів, і набір параметрів з максимальною правдоподібністю є найкращим вибором за доступних даних.

Конкретним розрахунком правдоподібності є ймовірність того, що буде призначено саме спостережуваний зразок, за припущення, що обрана модель та значення цих декількох параметрів θ дають точне наближення частотного розподілу сукупності, з якої було витягнуто цей спостережуваний зразок. Евристично має сенс, що добрим вибором параметрів є той, який видає для фактично спостережуваного зразка максимально можливу апостеріорну (лат. post-hoc) ймовірність трапляння. Теорема Уілкса визначає це евристичне правило кількісно, показуючи, що різниця між логарифмом правдоподібності, породженим значеннями параметрів оцінки, та логарифмом правдоподібності, породженим «істинними» (але невідомими) значеннями параметрів сукупності, має розподіл χ².

Оцінка максимальною правдоподібністю кожного незалежного зразка є окремою оцінкою «істинного» набору параметрів, що описує сукупність, з якої роблять вибірку. Послідовні оцінки від багатьох незалежних зразків гуртуватимуться разом з «істинним» набором значень параметрів сукупності, прихованим десь поміж них. Різницю між логарифмами максимальної правдоподібності та правдоподібностей суміжних наборів параметрів можна використовувати для малювання довірчої області на графіку, чиїми координатами є параметри θ₁... θ_p. Ця область оточує оцінку максимальною правдоподібністю, і всі точки (набори параметрів) всередині цієї області відрізняються в логарифмічній правдоподібності щонайбільше на якесь встановлене значення. Розподіл χ², заданий теоремою Уілкса, перетворює різниці логарифмічних правдоподібностей цієї області у «рівень довіри» до того, що «істинний» набір параметрів сукупності лежить всередині. Мистецтво обирання цієї встановленої різниці логарифмічних правдоподібностей полягає в тім, щоби робити рівень довіри прийнятно високим, в той же час тримаючи область прийнятно малою (вузька область оцінок).

В процесі спостерігання додаткових даних, замість використовувати їх для здійснення незалежних оцінок, їх можливо поєднувати з попередніми зразками в єдину об'єднану вибірку, і цю велику вибірку можливо використовувати для нової оцінки максимальною правдоподібністю. Зі збільшенням розміру цієї об'єднаної вибірки розмір області правдоподібності з таким же рівнем довіри скорочується. Врешті-решт, або розмір довірчої області стане майже єдиною точкою, або буде вибрано всю сукупність. В обох випадках, оцінений набір параметрів буде по суті таким же, як і набір параметрів сукупності.

У парадигмі ІКА правдоподібність інтерпретують у контексті теорії інформації.[54][55][56]