Циклічний граф (алгебра)
В теорії груп, яка є розділом абстрактної алгебри, циклічний граф групи ілюструє різні цикли групи і особливо корисний при візуалізації структури малих скінченних груп.
Цикл — це множина ступенів даного елемента групи a, де an, n-та ступень елементу a визначається як добуток, помножений на себе n раз. Елемент a називається генератором циклу. У скінченній групі деяка ненульова ступінь повинна бути нейтральним елементом e; така найменша ступінь є порядком циклу, тобто кількістю різних елементів циклу. У циклічному графі, цикл зображується у вигляді багатокутника, з вершинами, що представляють елементи групи, і сполучними лініями, що вказують, на те що всі елементи в цьому багатокутнику є членами одного і того ж циклу.
Цикли
Цикли можуть частково збігатися, або вони можуть не мати жодного спільного елемента, окрім нейтрального елемента. Граф циклу відображає кожен важливий цикл у вигляді многокутника.
Якщо a породжує цикл 6-го порядку (або, більш коротко, має порядок 6), то a6 = e. Тоді множина ступенів a2, {a2, a4, e} є циклом, але це очевидно. Аналогічно, a5 генерує той самий цикл, що і a.
Таким чином, потрібно розглядати тільки первісні цикли, а саме ті, що не є підмножинами іншого циклу. Кожен з них породжується деяким первісним елементом, a. Візьмемо вершину для кожного елемента вихідної групи. Для кожного первісного елемента, треба поєднати е і a, a вже з a2, …, an−1 з an і т. д., поки е не буде досягнуто. В результаті отримуємо циклічний граф.
Коли a2 = e, a має порядок 2 (це інволюція), і з'єднана з e двома ребрами. За винятком випадків, коли мета полягає в тому, щоб підкреслити, що маємо два ребра циклу, то граф, як правило, малюється[1] у вигляді однієї лінії між цими двома елементами.
Властивості
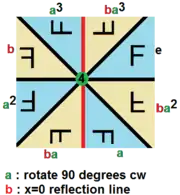 Dih4 калейдоскоп з червоним дзеркалом і 4-кратним генератором обертання |
 Циклічний граф для діедральної групи Dih4. |
Як приклад циклічного графу групи, розглянемо діедральну групу Dih4. Таблиця множення для цієї групи показана ліворуч, а цикл графу показано праворуч із зазначенням одиничного елементу e.
| o | e | b | a | a2 | a3 | ab | a2b | a3b |
|---|---|---|---|---|---|---|---|---|
| e | e | b | a | a2 | a3 | ab | a2b | a3b |
| b | b | e | a3b | a2b | ab | a3 | a2 | a |
| a | a | ab | a2 | a3 | e | a2b | a3b | b |
| a2 | a2 | a2b | a3 | e | a | a3b | b | ab |
| a3 | a3 | a3b | e | a | a2 | b | ab | a2b |
| ab | ab | a | b | a3b | a2b | e | a3 | a2 |
| a2b | a2b | a2 | ab | b | a3b | a | e | a3 |
| a3b | a3b | a3 | a2b | ab | b | a2 | a | e |
Зверніть увагу на цикл e, a, a2, a3. З таблиці множення можна побачити, що послідовні ступені поводяться так і у прямому, і у зворотньому порядку. Іншими словами: (a3)2=a2, (a3)3=a, і (a3)4=e. Така поведінка справедлива для будь-якого циклу в будь-якій групі — цикл може бути пройдений в будь-якому напрямку.
Цикли, які містять складене число елементів неявно містять цикли, які не показані в графі. Для графу Dih4 вище, ми могли б провести грань між a2 і e, так як (a2)2=e, але через те, що a2 є частиною більшого циклу, цього не можна зробити.
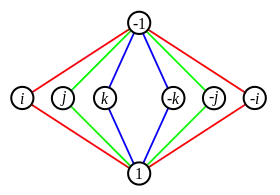
Існує поняття неоднозначності, коли два цикли мають спільний, не одиничний елемент. Розглянемо, наприклад, просту групу кватерніона, чий циклічний граф показаний праворуч. Кожен з елементів в середньому рядку при множенні на себе дає -1 (де 1 — це одиничний елемент). У цьому випадку ми можемо використовувати різні кольори для відстеження циклів. Як зазначалося раніше, два ребра 2-елементного циклу, як правило, представлені у вигляді одного рядка.
Обернений елемент можна знайти на циклічному графі у подібний спосіб. Це буде елемент, для якого відстань від одиничного елемента така сама, якщо рухатись по циклу у протилежному напрямку.
Історія
Циклічні графи досліджував числовий теоретик Даніель Шенкс на початку 1950-х років, як інструмент для вивчення мультиплікативних груп кільця лишків за модулем n.[2] Шенкс вперше опублікував цю ідею в 1962 у першому виданні своєї книги «Вирішені та невирішені проблеми в теорії чисел». [3] У книзі, Шенкс досліджує, які групи мають ізоморфні циклічні графи і, коли цикл є планарним графом.[4] У другому виданні 1978 року, Шенкс розмірковує про своє дослідження класових груп і розвиток алгоритму великих і малих кроків:[5]
Графи циклу виявилися корисними при роботі з кінцевими Абелевими групами; і я використовую їх часто в пошуку шлях навколо складної структури[77, p. 852], в отриманні розшукуваного мультиплікативного співвідношення [78, с. 426], або у виділенні певної розшукуваної підгрупи [79].
Графи циклу використовуються як педагогічний інструмент у підручнику Теорія візуальних груп Натана Картера.[6]
Графи циклів деяких сімейств групи
Певні типи груп дають типові графи:
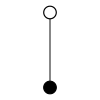
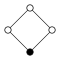
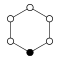
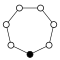
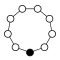
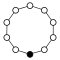
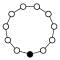
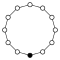
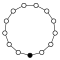
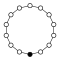
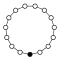
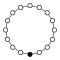
Циклічні групи Zn, порядку n, являють собою один цикл графу простого n-кутника з вершинами елементів.
 |
 |
 |
 |
 |
 |
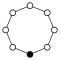 | |
| Z1 | Z2 = Dih1 | Z3 | Z4 | Z5 | Z6=Z3×Z2 | Z7 | Z8 |
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
| Z9 | Z10=Z5×Z2 | Z11 | Z12=Z4×Z3 | Z13 | Z14=Z7×Z2 | Z15=Z5×Z3 | Z16 |
 |
 |
 |
 |
 |
 |
 |
 |
| Z17 | Z18=Z9×Z2 | Z19 | Z20=Z5×Z4 | Z21=Z7×Z3 | Z22=Z11×Z2 | Z23 | Z24=Z8×Z3 |
 |
 |
 |
 |
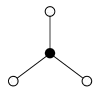
| Z2 | Z22 = Dih2 | Z23 = Dih2×Dih1 | Z24 = Dih22 |
|---|
При простому числі n, групи виду (Zn)m матимуть (nm − 1)/(n − 1) n-цикли, що ділять окремий елемент.
 |
 |
 |
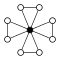 |
| Z22 = Dih2 | Z23 = Dih2×Dih1 | Z24 = Dih22 | Z32 |
|---|
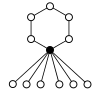
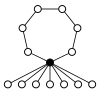
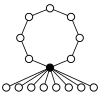
Діедральні групи Dihn, порядку 2n складаються з циклу n-елементу і n циклів 2-елементу.
 |
 |
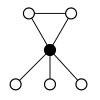 |
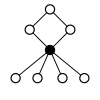 |
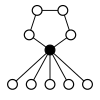 |
 |
 |
 |
 |
 |
| Dih1 = Z2 | Dih2 = Z22 | Dih3 | Dih4 | Dih5 | Dih6=Dih3×Z2 | Dih7 | Dih8 | Dih9 | Dih10=Dih5×Z2 |
|---|
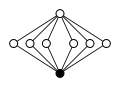
Біциклічні групи, Dicn = Q4n, порядку 4n.
 |
 |
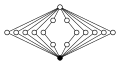 |
 |
|
| Dic2 = Q8 | Dic3 = Q12 | Dic4 = Q16 | Dic5 = Q20 | Dic6 = Q24 |
|---|
Інші прямі добутки:
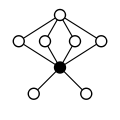 |
 |
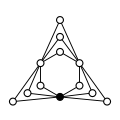 |
 |
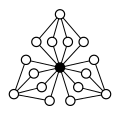 |
| Z4×Z2 | Z4×Z22 | Z6×Z2 | Z8×Z2 | Z42 |
|---|
Симетрична група — симетрична група Sn містить для будь-якої групи порядку n, підгрупу, ізоморфну цій групі. Таким чином, циклічний граф кожної групи порядку n можна знайти в циклічному графі Sn.
 A4×Z2 |
 S3 = Dih3 |
 S4 |
.svg.png.webp) Один з трьох Dih4, що знаходиться в S4 Те ж саме, що й |
Див. також
Посилання
- Weisstein, Eric W. Cycle Graph(англ.) на сайті Wolfram MathWorld.
- R. J. Mathar (2014). Plots of cycle graphs of the finite groups up to order 36.
Посилання
- Sarah Perkins (2000). Commuting Involution Graphs for A˜n, Section 2.2, p.3, first figure. Birkbeck College, Malet Street, London, WC1E 7HX: School of Economics, Mathematics and Statistics. Процитовано 31 січня 2016.
- Shanks, 1978, с. 246.
- Shanks, 1978, с. xii.
- Shanks, 1978, с. 83–98, 206–208.
- Shanks, 1978, с. 225.
- Carter, Nathan (2009). Visual Group Theory. Classroom Resource Materials. Mathematical Association of America. ISBN 978-0-88385-757-1.
- Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica 1990, § 4.2.3 Cycles, Stars, and Wheels, pp. 144—147
- Shanks, Daniel (1978) [1962]. Solved and Unsolved Problems in Number Theory (вид. 2nd). New York: Chelsea Publishing Company. ISBN 0-8284-0297-3.
- Pemmaraju, S. and Skiena, S. Computational Discrete Mathematics: Combinatorics and Graph Theory in Mathematics Cambridge, England: Cambridge University Press, 2003, § 6.2.4 Cycles, Stars, and Wheels pp. 248—249
