Група кватерніона

В теорії груп, група кватерніона є неабелевою групою порядку 8, ізоморфною множині восьми визначеним кватерніонам з операцією множення. Позначається Q₈ і представляється заданням групи

Q=\langle -1,i,j,k\mid \;\;(-1)^{2}=1,\;i^{2}=j^{2}=k^{2}=ijk=-1\rangle ,

Циклічний граф Q₈. Кожен колір це послідовність степенів деякого елемента, зв'язана з нейтральним елементом — (1). Для прикладу, червоний цикл показує, що i ² = −1, i ³ = −i та i ⁴ = 1. А також (−i )² = −1, (−i )³ = i та (−i )⁴ = 1.

де 1 (нейтральний елемент) та −1 комутують зі всіма елементами групи.

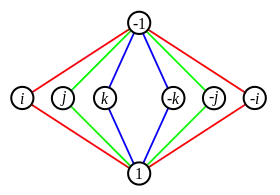
Множення елементів {±i, ±j, ±k} подібне до векторного добутку ортів в тривимірному евклідовому просторі.

{\begin{alignedat}{2}ij&=k,&\qquad ji&=-k,\\jk&=i,&kj&=-i,\\ki&=j,&ik&=-j.\end{alignedat}}

Властивості

Група кватерніона є гамільтоновою: Q₈ є неабелевою, але всі її підгрупи є нормальними.

Можна побудувати 4-вимірний дійсний векторний простір з базисом {1, i, j, k} і зробити з нього асоціативну алгебру ввівши множення, як описано вище, та добавивши дистрибутивний закон. Отримаємо тіло кватерніонів.

Порядок елементів i, j, k рівний 4, і довільні два з них утворюють породжуючу множину групи. Інше задання групи:

\langle x,y\mid x^{2}=y^{2},y^{-1}xy=x^{-1}\rangle .\,\!

Центр та комутант групи Q₈ це підгрупа {±1}.
- Факторгрупа Q/{±1} ізоморфна 4-групі Клейна V₄.
- Група внутрішніх автоморфізмів Q₈ також ізоморфна 4-групі Клейна.
- Повна група автоморфізмів Q₈ ізоморфна S₄, симетричній групі з 4 елементів.
- Група зовнішніх автоморфізмів Q₈ рівна S₄/V = S₃.

Матричне представлення

Група кватерніона може бути представлена як підгрупа загальної лінійної групи:

\ Q=\{\pm 1,\pm i,\pm j,\pm k\}\to \mathrm {GL} _{2}(\mathbb {C} )

де

1\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}

i\mapsto {\begin{pmatrix}{\sqrt {-1}}&0\\0&-{\sqrt {-1}}\end{pmatrix}}

j\mapsto {\begin{pmatrix}0&1\\-1&0\end{pmatrix}}

k\mapsto {\begin{pmatrix}0&{\sqrt {-1}}\\{\sqrt {-1}}&0\end{pmatrix}}

Всі матриці мають одиничний детермінант, тому це представлення Q₈ в спеціальну лінійну група SL₂(C).

Також важливим є представлення Q₈ в 8 елементів 2-векторного простору над скінченним полем F₃:

\ Q=\{\pm 1,\pm i,\pm j,\pm k\}\to \mathrm {GL} (2,3)

де

1\mapsto {\begin{pmatrix}1&0\\0&1\end{pmatrix}}

i\mapsto {\begin{pmatrix}1&1\\1&-1\end{pmatrix}}

j\mapsto {\begin{pmatrix}-1&1\\1&1\end{pmatrix}}

k\mapsto {\begin{pmatrix}0&-1\\1&0\end{pmatrix}}

де {−1,0,1} елементами з поля F₃. Всі матриці мають одиничний детермінант над F₃, тому це представлення Q₈ в спеціальну лінійну групу SL(2, 3). Насправді Q₈ є нормальною підгрупою SL(2, 3) індексу 3.

Див. також

Список малих груп

Джерела

Курош А. Г. Теория групп. — 3-е изд. — Москва : Наука, 1967. — 648 с. — ISBN 5-8114-0616-9.(рос.)
Кантор И. Л., Солодовников А. С. Гиперкомплексные числа. — Москва : Наука, 1973. — 144 с.(рос.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.