Циклічний порядок

У математиці, циклічний порядок являє собою спосіб організації множини об'єктів в колі. На відміну від більшості структур в теорії порядку, циклічний порядок не може бути змодельований як бінарне відношення «a < b». Циклічний порядок визначається як потрійне відношення [a, b, c], що означає «після a, досягається b перед c». Наприклад: [червень, жовтень, лютий]. Потрійне відношення називається циклічним порядком, якщо воно циклічне, асиметричне, транзитивне і повне. Якщо відношення неповне, то воно називається частковим циклічним порядком.

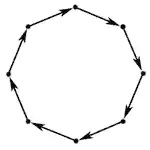
Множина з циклічним порядком називається циклічно впорядкованою множиною або просто циклом. Деякі цикли називаються дискретними. Вони мають тільки скінченний ряд елементів: є сім днів тижня, чотири сторони світу, дванадцять нот в хроматичній гамі, три можливі дії в грі камінь-ножиці-папір. У кінцевому циклі, кожен елемент має «наступний елемент» і «попередній елемент». Є також неперервно-мінливі цикли: нескінченні з багатьма елементами, як наприклад одиничне коло на площині.

Циклічні порядки тісно пов'язані з лінійними порядками, які організовують об'єкти в лінію. Будь-який лінійний порядок може бути зігнутий в коло і будь-який лінійний порядок може бути вирізаний в точці, у результаті чого утворюється лінія. Ці операції означають, що питання про циклічні порядки часто може бути перетворене в питання про лінійні порядки. Цикли мають більше симетрій, ніж лінійні порядки.

Кінцеві цикли
цикл з 5 елементів

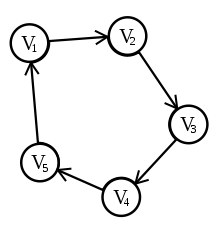
Циклічний порядок на множині X з n елементів, подібний до розташування X на циферблаті годинника, в n-годинному форматі. Кожен елемент х з X має «наступний елемент» і «попередній елемент», і беручи або наступні елементи, або попередні, можна обійти цикл точно один раз через всі елементи x(1), x(2), ..., x(n). Іншими словами, циклічний порядок на X схожий на перестановку, яка створює зі всіх елементів множини X єдиний цикл.

Істотне використання циклічних порядків знаходиться у визначенні спряжених класів вільних груп. Два елементи g і h вільної групи F на множині Y спряжені тоді і тільки тоді, коли вони записуються у вигляді добутку елементів y, y−1 з y в Y, а потім ці елементи включаються в циклічний порядок. Циклічний порядок еквівалентний щодо правил перезапису, які дозволяють видалити або додати сусідні y, y−1. Циклічний порядок на множині X може бути визначений лінійним порядком на X, але не єдиним чином. Вибір лінійного порядку еквівалентний вибору першого елементу, так що є рівно n лінійних порядків, які продукують даний циклічний порядок. Так як є n! можливих лінійних порядків, є (n − 1)! можливих циклічних порядків.

Означення

Нескінченна множина може також бути впорядкована циклічно. Прикладами нескінченних циклів можуть бути одиничне коло, S1, і раціональні числа, Q. Основна ідея та сама: ми розташовуємо велику кількість елементів по колу. Проте, в нескінченному випадку ми не можемо користуватися безпосереднім подальшим відношенням елементів; замість цього ми користуємося потрійним відношенням, яке означає, що елементи a, b, c з'являються один за одним (не обов'язково безпосередньо), оскільки ми йдемо по колу. З аргументів потрійного відношення [a, b, c] можна розглядати циклічний порядок як однопараметричне сімейство бінарних відношень порядку, які називаються розрізи, або двохпараметричним сімейством підмножин K, що носить назву інтервали.

Потрійне відношення

Загальне визначення виглядає наступним чином: циклічний порядок на множині X є відношення C ⊂ X3, написане [a, b, c], яке задовольняє наступним аксіомам:

  1. Циклічність: Якщо [a, b, c], то [b, c, a]
  2. Асиметрія: Якщо [a, b, c], то не [c, b, a]
  3. Транзитивність: якщо [a, b, c] і [a, c, d], то [a, b, d]
  4. Повнота: Якщо a, b, і c різні, то або [a, b, c] або [c, b, a]

Аксіоми названо по аналогії з аксіомами асиметрії, транзитивності та повноти для бінарного відношення, які разом визначають строгий лінійний порядок.

Розрізи та перестановки

Враховуючи лінійний порядок < на множині X, циклічний порядок на X індукованих < визначається наступним чином: [a, b, c] існують тоді і тільки тоді коли a < b < c або b < c < a або c < a < b

Два лінійні порядки викликають той самий циклічний порядок, коли вони можуть бути перетворені один в одний способом циклічної перестановки, як у колоді карт. Можна визначити циклічні відношення порядку, як потрійне відношення, індуковане строгим лінійним порядком як зазначено вище.

Вирізання однієї точки з циклічного порядку зберігає лінійний порядок. Точніше, маючи циклічно впорядковану множину (K, [ ]), кожен елемент якої a ∈ K визначає природний лінійний порядок <a на залишку множини K ∖ a за наступним правилом: x <a y тоді і тільки тоді, коли [a, x, y].

Крім того, <a може бути розширена додаванням як a найменшого елемента, отриманого лінійного порядку на K. Його називають головним розрізом з найменшим елементом a.

Інтервали

З урахуванням двох елементів a ≠ b ∈ K, відкритий інтервал від a до b, записується як (a, b), є множина всіх x ∈ K таких, що [a, x, b]. Система відкритих інтервалів повністю визначає циклічний порядок і може бути використана як альтернативне визначення циклічних відношень порядку.

Інтервал (a, b) має натуральний лінійний порядок <a. Можна визначити напівзакриті і закриті інтервали [a, b), (a, b] та [a, b] приєднанням a як найменшого елемента і/або b як найбільший елемент. Як окремий випадок відкритого інтервалу розглядається інтервал (a, a) і визначається як розріз K ∖ a.

В цілому, власна підмножина S з K називається опуклою, якщо вона містить інтервал між кожною парою точок: для a ≠ b ∈ S, або (a, b), або (b, a) і також є в S. Опуклу множину лінійно впорядковано розрізом <x для будь-якого x не в множині. Це впорядкування не залежить від вибору x.

Монотонні функції

«Циклічний порядок = організація в колі» — ідея, яка працює, тому що будь-яка підмножина циклу сама по собі є циклом. Для того, щоб користуватися цією ідеєю, щоб ввести циклічні порядки на множинах, які не є насправді підмножинами одиничного кола в площині, необхідно розглянути функції між множинами.

Функція між двома циклічно впорядкованими множинами f : X → Y називається монотонною функцією або гомоморфізмом, якщо вона визначає порядок на Y: всякий раз, коли [f(a), f(b), f(c)], має [a, b, c]. Еквівалентно, f монотонна, якщо кожного разу [a, b, c] і f(a), f(b), і f(c) всі різні, то [f(a), f(b), f(c)]. Типовий приклад монотонної функції — наступні функції на циклі з 6 елементів:

f(0) = f(1) = 4,
f(2) = f(3) = 0,
f(4) = f(5) = 1.

Функція називається вкладеною, якщо воно є монотонною і ін'єктивною. Еквівалентно, вкладена функція, яка призводить до порядку на X: якщо [a, b, c], то [f(a), f(b), f(c)]. Важливим прикладом є те, що якщо X є підмножиною циклічно впорядкованої множини Y і X має свій природний порядок, то i : X → Y є вкладенням. Загалом, ін'єктивна функція f з невизначеної множини X в циклі Y індукує унікальний циклічний порядок на X, який робить f вкладенням.

Додаткові конструкції

Розгортання циклу

Починаючи з циклічно впорядкованої множини K можна утворити лінійний порядок розгорнувши його вздовж нескінченної лінії. Це відображає інтуїтивне поняття відстеження скільки разів ми проходимо по колу. Формально лінійний порядок визначається на декартовому добутку Z × K, де Z це множина цілих чисел, які утворені шляхом фіксації елементів a і вимагаючи, щоб для всіх i:

Якщо [a, x, y], то ai < xi < yi < ai + 1.

Наприклад, місяці січня 2022, травня 2022, вересня 2022, і січня 2023 відбуватимуться в такому порядку.

Зворотна побудова починається з лінійно упорядкованої множини і скручує її в циклічно впорядковану множину. Маючи лінійно впорядковану множину L і бієкцію T : L → L, яка зберігає порядок, з необмеженими орбітами, орбіти простору L / T циклічно відсортовані за вимогою:

Якщо a < b < c < T(a), то [[a], [b], [c]].

Зокрема, можна поновити K шляхом визначення T(xi) = xi + 1 on Z × K.

Лексикографічний добуток

Маючи циклічно впорядковану множину (K, [ ]) і лінійно упорядковану множину (L, <), (повний) лексикографічний добуток — це циклічний порядок на добутку множин K × L, визначається як [(a, x), (b, y), (c, z)], якщо виконуються наступні твердження:

  • [a, b, c]
  • a = b ≠ c and x < y
  • b = c ≠ a and y < z
  • c = a ≠ b and z < x
  • a = b = c and [x, y, z]

Лексикографічний добуток K × L глобально виглядає як K і локально виглядає як L, він може розглядатися як K копій L. Ця конструкція іноді використовується для опису циклічно впорядкованих груп.

Пов'язані структури

Групи

Циклічно впорядкована група — множина як з груповою структурою, так і з циклічним порядком, що лівий і правий добуток зберігає циклічний порядок. Циклічно впорядковані групи уперше глибоко вивчав Ладіслав Рігер в 1947 році. Вони є узагальненням циклічних груп: нескінченної циклічної групи Z і скінченної циклічної групи Z/n. Так як лінійний порядок індукує циклічний порядок, циклічно впорядковані групи є також узагальненням лінійно впорядкованих груп: дійсні числа R, раціональні числа Q тощо. Деякі з найбільш важливих циклічно впорядкованих груп не потрапляють до попередньої категорії: циклічна група T і її підгрупи, такі як підгрупа раціональних точок.

Див. також

Посилання
Список літератури

Додаткові матеріали
  • Bhattacharjee, Meenaxi; Macpherson, Dugald; Möller, Rögnvaldur G.; Neumann, Peter M. (1998). Notes on Infinite Permutation Groups. Lecture Notes in Mathematics 1698. Springer. с. 108–109. doi:10.1007/BFb0092550.
  • Bodirsky, Manuel; Pinsker, Michael (to appear). Reducts of Ramsey Structures. Model Theoretic Methods in Finite Combinatorics. Contemporary Mathematics. AMS. arXiv:1105.6073.
  • Cameron, Peter J. (June 1976). Transitivity of permutation groups on unordered sets. Mathematische Zeitschrift 148 (2): 127–139. doi:10.1007/BF01214702.
  • Cameron, Peter J. (June 1977). Cohomological aspects of two-graphs. Mathematische Zeitschrift 157 (2): 101–119. doi:10.1007/BF01215145.
  • Courcelle, Joost; Engelfriet (April 2011). Graph Structure and Monadic Second-Order Logic, a Language Theoretic Approach. Cambridge University Press. Процитовано 17 травня 2011.
  • Droste, M.; Giraudet, M.; Macpherson, D. (March 1995). Periodic Ordered Permutation Groups and Cyclic Orderings. Journal of Combinatorial Theory, Series B 63 (2): 310–321. doi:10.1006/jctb.1995.1022.
  • Ivanov, A. A. (January 1999). Finite Covers, Cohomology and Homogeneous Structures. Proceedings of the London Mathematical Society 78 (1): 1–28. doi:10.1112/S002461159900163X.
  • Kennedy, Christine Cowan (August 1955). On a cyclic ternary relation ... (M.A. Thesis). Tulane University. OCLC 16508645.
  • Kónya, Eszter Herendine (2006). A mathematical and didactical analysis of the concept of orientation. Teaching Mathematics and Computer Science 4 (1): 111–130. Архів оригіналу за 26 липня 2011. Процитовано 17 травня 2011.
  • Kónya, Eszter Herendine (2008). Geometrical transformations and the concept of cyclic ordering. У Maj, Bożena; Pytlak, Marta; Swoboda, Ewa. Supporting Independent Thinking Through Mathematical Education. Rzeszów University Press. с. 102–108. ISBN 978-83-7338-420-0. Процитовано 17 травня 2011.
  • Leloup, Gérard (February 2011). Existentially equivalent cyclic ultrametric spaces and cyclically valued groups. Logic Journal of the IGPL 19 (1): 144–173. doi:10.1093/jigpal/jzq024. Процитовано 30 квітня 2011.
  • Marongiu, Gabriele (1985). Some remarks on the ℵ0-categoricity of circular orderings. Unione Matematica Italiana. Bollettino. B. Serie VI (Italian) 4 (3): 883–900. MR 0831297.
  • McCleary, Stephen; Rubin, Matatyahu (6 жовтня 2005). Locally Moving Groups and the Reconstruction Problem for Chains and Circles. arXiv:math/0510122.
  • Müller, G. (1974). Lineare und zyklische Ordnung. Praxis der Mathematik 16: 261–269. MR 0429660.
  • Rubin, M. (1996). Locally moving groups and reconstruction problems. У Holland, W. Charles. Ordered groups and infinite permutation groups. Mathematics and Its Applications 354. Kluwer. с. 121–157. ISBN 978-0-7923-3853-6.
  • Świerczkowski, S. (1956). On cyclic ordering relations. Bulletin de l'Académie Polonaise des Sciences, Classe III 4: 585–586.
  • Świerczkowski, S. (1959b). On cyclically ordered intervals of integers. Fundamenta Mathematicae 47: 167–172. Процитовано 2 травня 2011.
  • Truss, J.K. (July 1992). Generic Automorphisms of Homogeneous Structures. Proceedings of the London Mathematical Society. s3-65 (1): 121–141. doi:10.1112/plms/s3-65.1.121.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.